Network Flow algorithm is involved in this problem.

The ancient city of Rome had a complex network of aqueducts delivering water to public buildings and to those residents important enough to have plumbing in their homes. Suppose some new baths

are being built, so the Roman engineers need to increase the maximum water flow that their network

of aqueducts can carry - however, theyve pillaged too few barbaric villages recently, so the engineers must keep costs down by replacing only one aqueduct segment. That is, if G is the directed graph representing the network of aqueducts, they are only allowed to increase the capacity of a single arc in the entire graph. Let f be a max flow for G of value v(f), let Gr(f) be the corresponding residual graph, and let (A,B) be a min cut where A is the set of vertices reachable from the source s in Gr(f).

DISCLAIMER

You know the drill. You have to justify everything. For network flow problems the general idea is that given a specific input you will construct a specific graph (that depends on the input) such that the value of the maximum flow on your graph (or whether a circulation is possible) allows you to determine the answer to the input problem. You are strongly encouraged to draw a picture of your graph as part of your answer. If you typeset your homework (thank you), it will probably be faster to just typeset all the text first, leave enough white space for a drawing, and just do the drawing by hand (after having drawn a draft, in a separate piece of paper, at least once). Now, regarding the meat of the matter, i.e., what are you supposed to say. Well, its obvious. You will be making claims of the following type: if the maximum flow in this graph is greater or equal to blah, then the kids will not complain, but if it is less than blah they will. So, you are to prove two separate things. That is, (i) how from a flow of blah or more you can construct an assignment of cows to troughs that does not cause a complaint and, (ii) how the non-existence of a flow of blah or more proves the unavoidability of the complaint. For (ii) it will typically be more straightforward to establish the contapositive (recall that the contrapositive of a b is not(b) 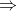not(a) and it is logically equivalent to a 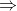b). In this case, it amounts to showing how given an assignment that does not cause a complaint, you could create a flow of value at least blah.