No matter what I do, the application reduces the resolution of the photo. I can send it to you via another way if you send your mail adress. you can mark this question as solved from here

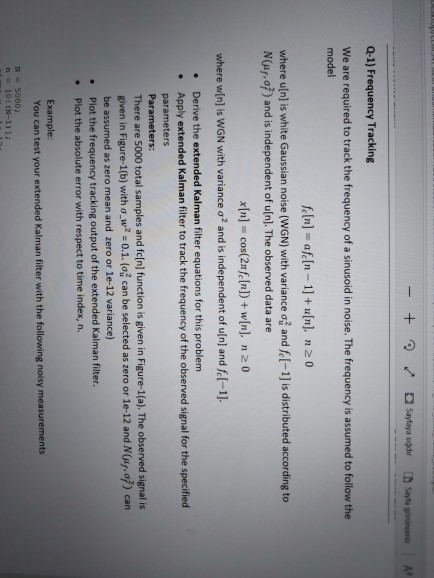
Q-1) Frequency Tracking We are required to track the frequency of a sinusoid in noise. The frequency is assumed to follow the model feIm] = afein - 1] +u[n], 120 where u[n] is white Gaussian noise (WGN) with variance and fel-1) is distributed according to N647,07) and is independent of un). The observed data are x[n] = cos(2nf InD+ winl. 120 where win] is WGN with variance and is independent of un) and fel-1). Derive the extended Kalman filter equations for this problem Apply extended Kalman filter to track the frequency of the observed signal for the specified parameters Parameters: There are 5000 total samples and feln) function is given in Figure-1(a). The observed signal is given in Figure-1(b) with C_w?=0.1. (o can be selected as zero or 1e-12 and NCHY ) can be assumed as zero mean and zero or le-12 variance) Plot the frequency tracking output of the extended Kalman filter Plot the absolute error with respect to time index, n. Example: You can test your extended Kalman filter with the following noisy measurements N-50001 - 10:(N-111: signa - 10-12; signa - le-ti E - (0.001s (1.8/2) -0.001 (N/2+1:end)/(8/8) + agrt sigma_u) *rand 11,3) - coa (2*pi*. - sqrt (signa_w) *rand (1,1) 3.5 (pel Skoubou 2 15 05 -05! 500 3000 3500 4000 4500 5000 1000 discrete time in Figure-1(a): fcin function noisy measurements desired signal 05 30H - 15 25 500 3500 2000 n (sample index) Figure-1(b): noisy x[n] function and the desired sinusoidal signal, cos(2xfcin) Sayfaya sadir A Q-1) Frequency Tracking We are required to track the frequency of a sinusoid in noise. The frequency is assumed to follow the model fe[n] = afein - 1] + [n], n20 where u[n] is white Gaussian noise (WGN) with variance and fel-1) is distributed according to Nup.0) and is independent of u[n]. The observed data are x[n] - cos(2nfo[n]) + w[n]. n20 where win) is WGN with variance o? and is independent of u[n) and fel-1). Derive the extended Kalman filter equations for this problem Apply extended Kalman filter to track the frequency of the observed signal for the specified parameters Parameters: There are 5000 total samples and fe(n) function is given in Figure-1(a). The observed signal is given in Figure-1(b) with a_W2 = 0.1. (o can be selected as zero or le-12 and Nup.0) can be assumed as zero mean and zero or le-12 variance) Plot the frequency tracking output of the extended Kalman filter. Plot the absolute error with respect to time index, n. Example: You can test your extended Kalman filter with the following noisy measurements N = 5000; n = 10: (N-1) Q-1) Frequency Tracking We are required to track the frequency of a sinusoid in noise. The frequency is assumed to follow the model feIm] = afein - 1] +u[n], 120 where u[n] is white Gaussian noise (WGN) with variance and fel-1) is distributed according to N647,07) and is independent of un). The observed data are x[n] = cos(2nf InD+ winl. 120 where win] is WGN with variance and is independent of un) and fel-1). Derive the extended Kalman filter equations for this problem Apply extended Kalman filter to track the frequency of the observed signal for the specified parameters Parameters: There are 5000 total samples and feln) function is given in Figure-1(a). The observed signal is given in Figure-1(b) with C_w?=0.1. (o can be selected as zero or 1e-12 and NCHY ) can be assumed as zero mean and zero or le-12 variance) Plot the frequency tracking output of the extended Kalman filter Plot the absolute error with respect to time index, n. Example: You can test your extended Kalman filter with the following noisy measurements N-50001 - 10:(N-111: signa - 10-12; signa - le-ti E - (0.001s (1.8/2) -0.001 (N/2+1:end)/(8/8) + agrt sigma_u) *rand 11,3) - coa (2*pi*. - sqrt (signa_w) *rand (1,1) 3.5 (pel Skoubou 2 15 05 -05! 500 3000 3500 4000 4500 5000 1000 discrete time in Figure-1(a): fcin function noisy measurements desired signal 05 30H - 15 25 500 3500 2000 n (sample index) Figure-1(b): noisy x[n] function and the desired sinusoidal signal, cos(2xfcin) Sayfaya sadir A Q-1) Frequency Tracking We are required to track the frequency of a sinusoid in noise. The frequency is assumed to follow the model fe[n] = afein - 1] + [n], n20 where u[n] is white Gaussian noise (WGN) with variance and fel-1) is distributed according to Nup.0) and is independent of u[n]. The observed data are x[n] - cos(2nfo[n]) + w[n]. n20 where win) is WGN with variance o? and is independent of u[n) and fel-1). Derive the extended Kalman filter equations for this problem Apply extended Kalman filter to track the frequency of the observed signal for the specified parameters Parameters: There are 5000 total samples and fe(n) function is given in Figure-1(a). The observed signal is given in Figure-1(b) with a_W2 = 0.1. (o can be selected as zero or le-12 and Nup.0) can be assumed as zero mean and zero or le-12 variance) Plot the frequency tracking output of the extended Kalman filter. Plot the absolute error with respect to time index, n. Example: You can test your extended Kalman filter with the following noisy measurements N = 5000; n = 10: (N-1)