node.h:

#pragma once #include  using namespace std; class node { public: private: int key; // search key string data; // data stored for this key node * left; // pointer to the BST left child (all keys  this key) }; 

tst.h:

//-------------------------------------------------------------------- // class tst //-------------------------------------------------------------------- // Describes a Trinary Search Tree, a variation of a Binary Search // Tree where each node (in addition to a left and right subtree) // has a linked list of nodes with the same key value, // where the most-recent value for the key is stored in the BST node // and the older nodes are stored in a linked list in historical order //-------------------------------------------------------------------- #pragma once #include  #include "node.h" using namespace std; class tst { public: tst(); // constructor ~tst(); // destructor void insert(int k, string s); // insert new node with given key/data void print(); // print the TST int height(); // returns the Tree Height int count(); // returns number of BST nodes int fullCount(); // returns number of all nodes string search(int k); // returns current and historical data void read(); // reads data from a file int maxKey(); // returns the largest key in the tree private: void print(node * r, int level); void insert(node * p, node * r, node * rParent); // suggested void insertEqual(node *p, node *r, node * rParent); // suggested node * root; }; 

tst.cpp:

#include  #include  #include  #include "tst.h" using namespace std; //-------------------------------------------------------------------- // Constructor/Destructor //-------------------------------------------------------------------- //-------------------------------------------------------------------- // insert - public //-------------------------------------------------------------------- // given a new key and data, allocates and populates a new node // When the tree is empty, makes the new node the root // When the tree is not empty, inserts the new node into the root // (parent of root is NULL) //-------------------------------------------------------------------- void tst::insert(int k, string s) { } // public //-------------------------------------------------------------------- // insert - private //-------------------------------------------------------------------- // given: pointer to a newly-allocated and populated node to insert // pointer to the tree/subtree into which the new node is to // be inserted // pointer to the parent of r. The parent's right or left // child will need to be modified if this is a // "duplicate" key, as the new node replaces the // current node (r) in the tree. //-------------------------------------------------------------------- void tst::insert(node * p, node * r, node * rParent) { // if the new node's key is LESS THAN r's key, // insert new node on the LEFT side of r. if (p->key key) { if (r->left != NULL) // r already has a left child //WRITE THIS LINE! // insert new node into r's left child else // else r has no left child //WRITE THIS LINE! // make p the new left child } else if (p->key > r->key) { // FINISH THIS!! } else insertEqual(p, r, rParent); } // insert() //-------------------------------------------------------------------- // insert - private //-------------------------------------------------------------------- // Sub method of insert()-private // p's key and r's key are equal, so p's node will replace r's in the // BST. //-------------------------------------------------------------------- void tst::insertEqual(node *p, node *r, node * rParent) { } //-------------------------------------------------------------------- // maxKey //-------------------------------------------------------------------- // returns the highest key in the tree, or -1 for an empty tree int tst::maxKey() { } //-------------------------------------------------------------------- // print //-------------------------------------------------------------------- void tst::print() { cout right, level + 1); // print this node for (int i = 0; i key data; // print the equal nodes of this node node * p = r->equal; while (p != NULL) { cout data; p = p->equal; } cout left, level + 1); } // print() //-------------------------------------------------------------------- // read //-------------------------------------------------------------------- void tst::read() { ifstream f; int k; string data; // open input file cout > data; f.open(data); if (f.fail()) { cout > k; f.ignore(); getline(f, data); while (k != -1) { // while not sentinel value insert(k, data); // insert data into TST f >> k; // read next record f.ignore(); getline(f, data); } f.close(); } // read() //-------------------------------------------------------------------- // height //-------------------------------------------------------------------- int tst::height() { } //-------------------------------------------------------------------- // count //-------------------------------------------------------------------- // returns the number of nodes in the BST, not including the nodes // in the equal lists int tst::count() { } //-------------------------------------------------------------------- // fullCount //-------------------------------------------------------------------- // returns the number of nodes in the entire structure, including the // nodes in the equal lists. int tst::fullCount() { } //-------------------------------------------------------------------- // search //-------------------------------------------------------------------- // given: a key to search for // returns: When found: a string with the current data, with the data // for any equal nodes appended with a :: between each value. // When not found: returns "NOT FOUND" //-------------------------------------------------------------------- string tst::search(int k) { } 

main.cpp:

//--------------------------------------------------------------------- // CS 215 - Fall 2017 // Project 4 - Trinary Search Tree //--------------------------------------------------------------------- // Completed By: // Section: // I receive help from: //--------------------------------------------------------------------- #include  #include  #include  #include "tst.h" char getOption() { string option; cout  "; cin >> option; return toupper(option[0]); } // getOption() void doInsert(tst & t) { int key; string data; cout > key; cout > key; cout  
search.txt:
 
//----------------------------------------------------------------- // search //----------------------------------------------------------------- // Given: a key to search for // Returns: current and past data for this key, when found // or "NOT FOUND" //----------------------------------------------------------------- // just invoke the recursive method,starting with the root of the TST string tst::search(int k) { return search(k, root); } // node * r - a pointer to the root of the tree OR SUBTREE string tst::search(int k, node * r) { string s; // BASE CASE 1: if the subtree is EMPTY, there is nothing to search if () { // TODO: finish the if() s = "NOT FOUND"; } // BASE CASE 2: if found, build the data string to return else if () { // TODO: finish the if() s = r->data; node * p = r->equal; while (p != NULL) { s = s + "::" + p->data; p = p->equal; } } // ELSE not found in this node. do we go right or left?? else if () // TODO: finish the if() // TODO: go right...set s to the "answer" else // TODO: go left...set s to the "answer" // all 4 cases set s to "the answer". Return it. return s; } // search() 
 
tst.txt:
 
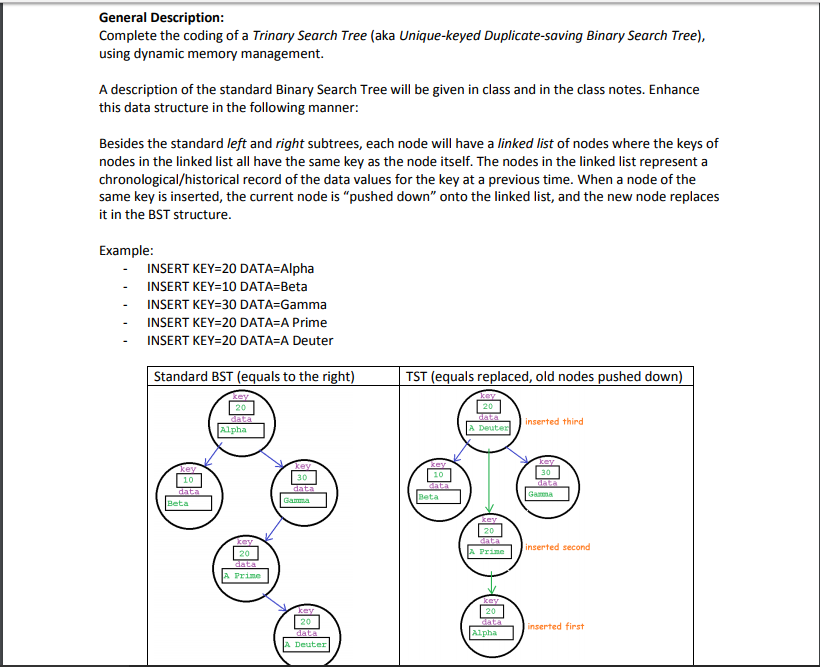
150 One Fifty 130 One Thirty 170 One Seventy 120 One Twenty 140 One Forty 160 One Sixty 180 One Eighty -1 End of data 
  General Description Complete the coding of a Trinary Search Tree (aka Unique-keyed Duplicate-saving Binary Search Tree) using dynamic memory management. A description of the standard Binary Search Tree will be given in class and in the class notes. Enhance this data structure in the following manner: Besides the standard left and right subtrees, each node will have a linked list of nodes where the keys of nodes in the linked list all have the same key as the node itself. The nodes in the linked list represent a chronological/historical record of the data values for the key at a previous time. When a node of the same key is inserted, the current node is "pushed down" onto the linked list, and the new node replaces it in the BST structure Example INSERT KEY 20 DATA Alpha INSERT KEY-10 DATA-Beta INSERT KEY-30 DATA=Gamma INSERT KEY-20 DATA=A Prime INSERT KEY-20 DATA=A Deuter Standard BST (equals to the right) TST (equals replaced, old nodes pushed down) 20 Alpha Deuterted third 10 Beta Prineinserted second rine inserted first Alpha Deuter