
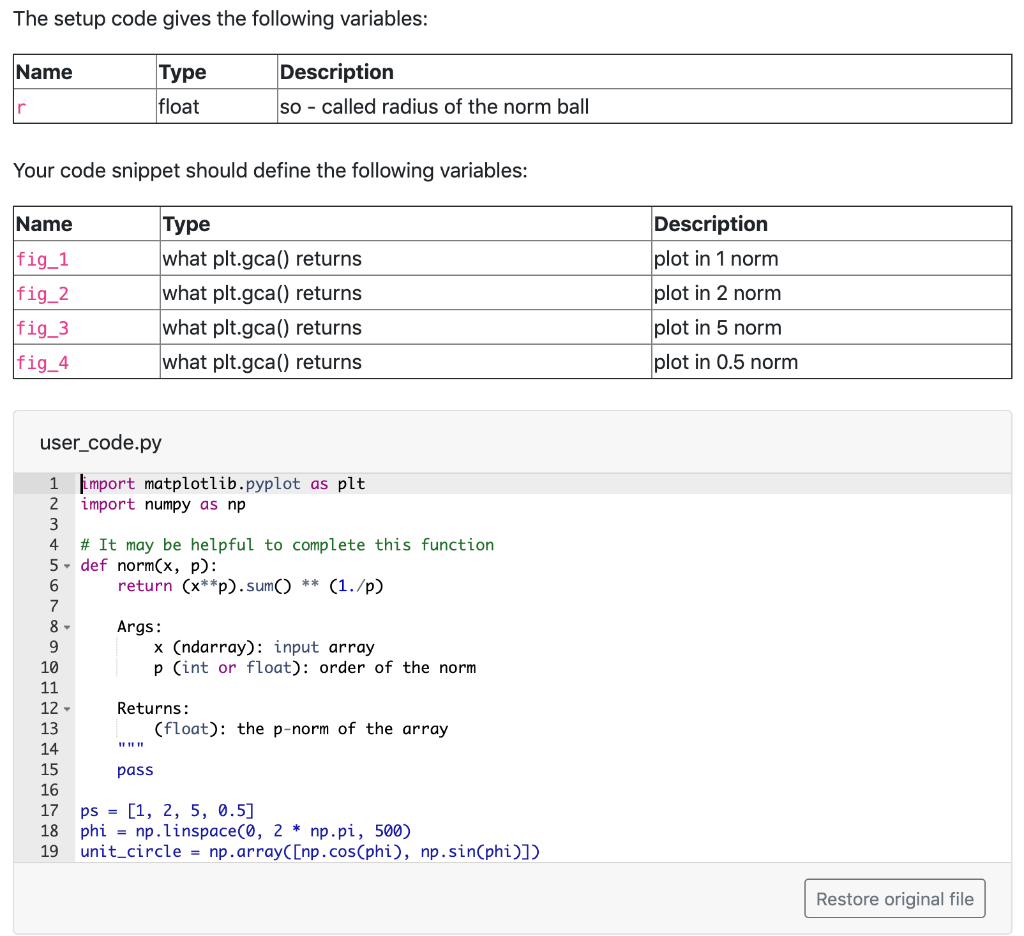
Norms Note: In addition to regular p-norms, we will use the "0.5-norm" below. By this we mean that you should use the expression for the p-norm with p = 0.5. Note that this is not actually a norm. Your task: With respect to each norm, plot a 2D ball with radius r centered around the origin using 500 points. (That is, plot the ball made of all 2D vectors w that satisfy the equation (wl=r for the p-norm.) Save a plot's axes using plt.gca(). For example: plt. figure() # ... code for the plot... fig_1 = plt.gca() Your code should produce the following four plots: 1. Draw the radius r 2D ball with respect to the 1-norm and save the plot to fig_1. 2. Draw the radius r 2D ball with respect to the 2-norm and save the plot to fig_2. 3. Draw the radius r 2D ball with respect to the 5-norm and save the plot to fig_3. 4. Draw the radius r 2D ball with respect to the "0.5-norm" and save the plot to fig_4. The setup code gives the following variables: Name Type float Description so-called radius of the norm ball Your code snippet should define the following variables: Name fig_1 fig_2 fig_3 fig_4 Type what plt.gca() returns what plt.gca() returns what plt.gca() returns what plt.gca() returns Description plot in 1 norm plot in 2 norm plot in 5 norm plot in 0.5 norm user_code.py 1 2 import matplotlib.pyplot as plt import numpy as np 4 # It may be helpful to complete this function 5- def norm(x, p): return (***p). sum() ** (1./p) Args: x (ndarray): input array p (int or float): order of the norm 12 Returns: (float): the p-norm of the array pass 17 ps = [1, 2, 5, 0.5] phi = np.linspace(0, 2 * np.pi, 500) unit_circle = n .array([np.cos(phi), np.sin(phi)]) 19 Restore original file Norms Note: In addition to regular p-norms, we will use the "0.5-norm" below. By this we mean that you should use the expression for the p-norm with p = 0.5. Note that this is not actually a norm. Your task: With respect to each norm, plot a 2D ball with radius r centered around the origin using 500 points. (That is, plot the ball made of all 2D vectors w that satisfy the equation (wl=r for the p-norm.) Save a plot's axes using plt.gca(). For example: plt. figure() # ... code for the plot... fig_1 = plt.gca() Your code should produce the following four plots: 1. Draw the radius r 2D ball with respect to the 1-norm and save the plot to fig_1. 2. Draw the radius r 2D ball with respect to the 2-norm and save the plot to fig_2. 3. Draw the radius r 2D ball with respect to the 5-norm and save the plot to fig_3. 4. Draw the radius r 2D ball with respect to the "0.5-norm" and save the plot to fig_4. The setup code gives the following variables: Name Type float Description so-called radius of the norm ball Your code snippet should define the following variables: Name fig_1 fig_2 fig_3 fig_4 Type what plt.gca() returns what plt.gca() returns what plt.gca() returns what plt.gca() returns Description plot in 1 norm plot in 2 norm plot in 5 norm plot in 0.5 norm user_code.py 1 2 import matplotlib.pyplot as plt import numpy as np 4 # It may be helpful to complete this function 5- def norm(x, p): return (***p). sum() ** (1./p) Args: x (ndarray): input array p (int or float): order of the norm 12 Returns: (float): the p-norm of the array pass 17 ps = [1, 2, 5, 0.5] phi = np.linspace(0, 2 * np.pi, 500) unit_circle = n .array([np.cos(phi), np.sin(phi)]) 19 Restore original file








