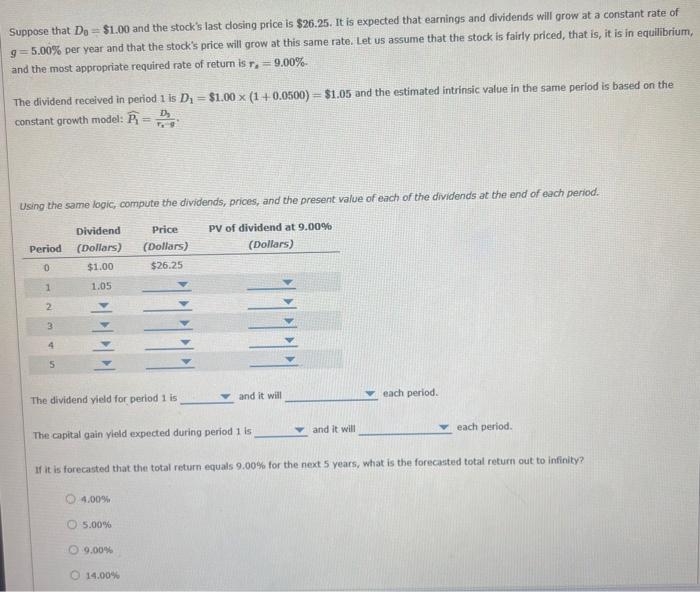
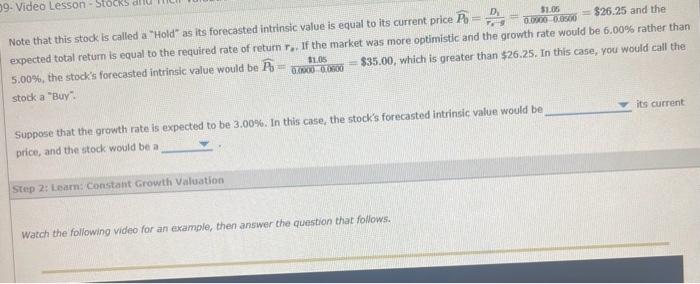
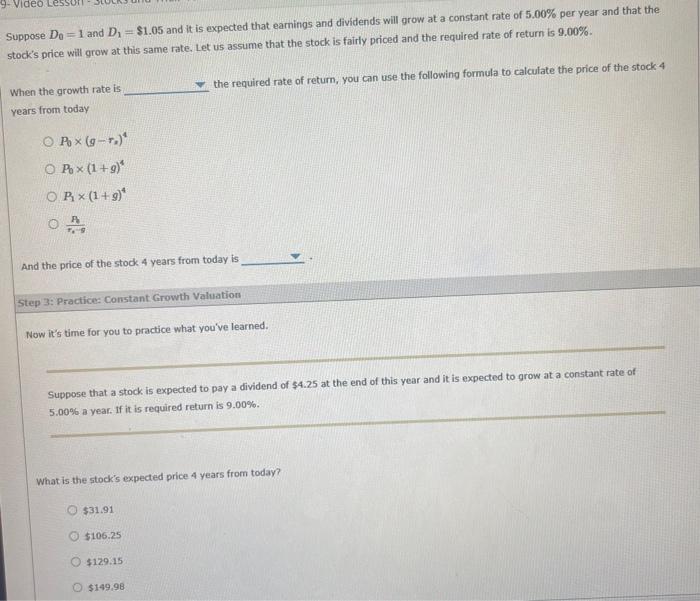
Note that this stock is called a "Hold" as its forecasted intrinsic value is equal to its current price P0=rrgD1=0.00000.0300$100=$26.25 and the expected total return is equal to the required rate of return r2. If the market was more optimistic and the growth rate would be 6.00% rather than 5.00%, the stock's forecasted intrinsic value would be P0=0.00000.050011.05=$35.00, which is oreater than $26.25. In this case, you would call the stock a "Bur: suppose that the growth rate is expected to be 3.00%. In this case, the stock's forecasted intrinsic value would be its current price, and the stock would be a Suppose that D0=$1.00 and the stock's last dosing price is $26.25. It is expected that earnings and dividends will grow at a constant rate of g=5.00% per year and that the stock's price will grow at this same rate. Let us assume that the stock is fairly priced, that is, it is in equilibrium, and the most appropriate required rate of retum is r2=9.00% - The dividend received in period 1 is D1=$1.00(1+0.0500)=$1.05 and the estimated intrinsic value in the same period is based on the constant growth model: P1=r33D3. Using the same logic, compute the dividends, prices, and the present value of each of the dividends at the end of each period. The dividend vield for period 1 is and it will each period. The capital gain vield expected during period 1 is and it will each period. If it is forecasted that the total return equals 9.00% for the next 5 years, what is the forecasted total return out to infinity? 4.00% 5.00% 9.00% 14.00% Suppose D0=1 and D1=$1.05 and it is expected that earnings and dividends will grow at a constant rate of 5.00% per year and that the stock's price will grow at this same rate. Let us assume that the stock is fairly priced and the required rate of return is 9.00%. When the growth rate is the required rate of return, you can use the following formula to calculate the price of the stock 4 years from today P0(gr2)4P0(1+g)4P1(1+g)4F,gA And the price of the stock 4 years from today is Step 3: Practice: Constant Grow th Vatiation Now it's time for you to practice what you've learned. Suppose that a stock is expected to pay a dividend of $4.25 at the end of this year and it is expected to grow at a constant rate of 5.00% a year. If it is required return is 9.00%. What is the stock's expected price 4 years from today? $31.91 $106.25 $120.15 $149,98