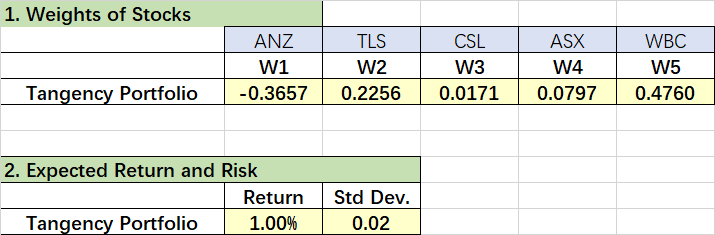
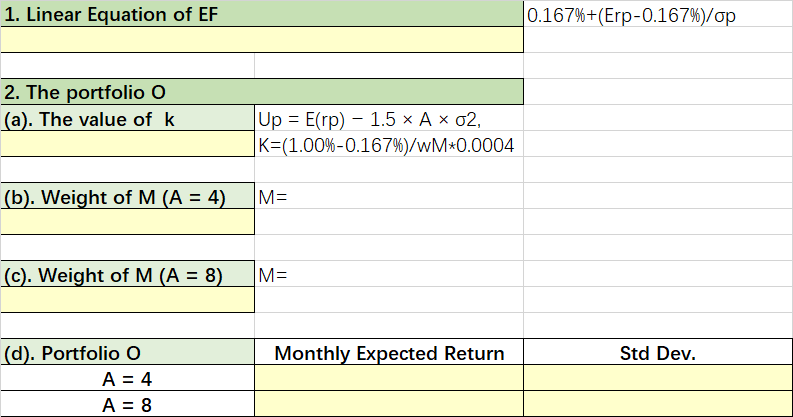
Now consider the EF that represents all portfolios consisting of both the risk-free asset and the 5 selected stocks. 4 1. What is the mathematical linear equation for the EF if the annual risk-free rate is 2%? Thus, express monthly expected return in terms of risk (as measured by standard deviation). H 2. Consider the optimal portfolio O (with highest achievable utility) on the EF.- 2 (a) The proportion of the funds allocated to the tangency portfolio M in the optimal portfolio O can be expressed as (2) WM E(RM Rp) kAOM 2 What is the value of k in equation (2)? Detail the computation of this value - (b) If the risk aversion coefficient A = 4, compute the proportion of the funds allocated to M. [1 mark] (c) Compute the proportion of the funds allocated to M for A = 8.4 (d) Calculate the monthly expected return of the optimal portfolio O and its risk (standard deviation) when A = 4 and A = 8, respectively. Discuss your findings . + 1. Weights of Stocks ANZ W1 -0.3657 TLS W2 0.2256 CSL W3 0.0171 ASX W4 0.0797 WBC W5 0.4760 Tangency Portfolio 2. Expected Return and Risk Return Tangency Portfolio 1.00% Std Dev. 0.02 4. Sharpe Ratio 4.67 1. Linear Equation of EF 0.167%+(Erp-0.167%)/op 2. The portfolio O (a). The value of k Up = E(rp) - 1.5 x A x 02, K=(1.00%-0.167%)/WM*0.0004 (b). Weight of M (A = 4). M= (c). Weight of M (A = 8) M= Monthly Expected Return Std Dev. (d). Portfolio o A = 4 A = 8 Now consider the EF that represents all portfolios consisting of both the risk-free asset and the 5 selected stocks. 4 1. What is the mathematical linear equation for the EF if the annual risk-free rate is 2%? Thus, express monthly expected return in terms of risk (as measured by standard deviation). H 2. Consider the optimal portfolio O (with highest achievable utility) on the EF.- 2 (a) The proportion of the funds allocated to the tangency portfolio M in the optimal portfolio O can be expressed as (2) WM E(RM Rp) kAOM 2 What is the value of k in equation (2)? Detail the computation of this value - (b) If the risk aversion coefficient A = 4, compute the proportion of the funds allocated to M. [1 mark] (c) Compute the proportion of the funds allocated to M for A = 8.4 (d) Calculate the monthly expected return of the optimal portfolio O and its risk (standard deviation) when A = 4 and A = 8, respectively. Discuss your findings . + 1. Weights of Stocks ANZ W1 -0.3657 TLS W2 0.2256 CSL W3 0.0171 ASX W4 0.0797 WBC W5 0.4760 Tangency Portfolio 2. Expected Return and Risk Return Tangency Portfolio 1.00% Std Dev. 0.02 4. Sharpe Ratio 4.67 1. Linear Equation of EF 0.167%+(Erp-0.167%)/op 2. The portfolio O (a). The value of k Up = E(rp) - 1.5 x A x 02, K=(1.00%-0.167%)/WM*0.0004 (b). Weight of M (A = 4). M= (c). Weight of M (A = 8) M= Monthly Expected Return Std Dev. (d). Portfolio o A = 4 A = 8