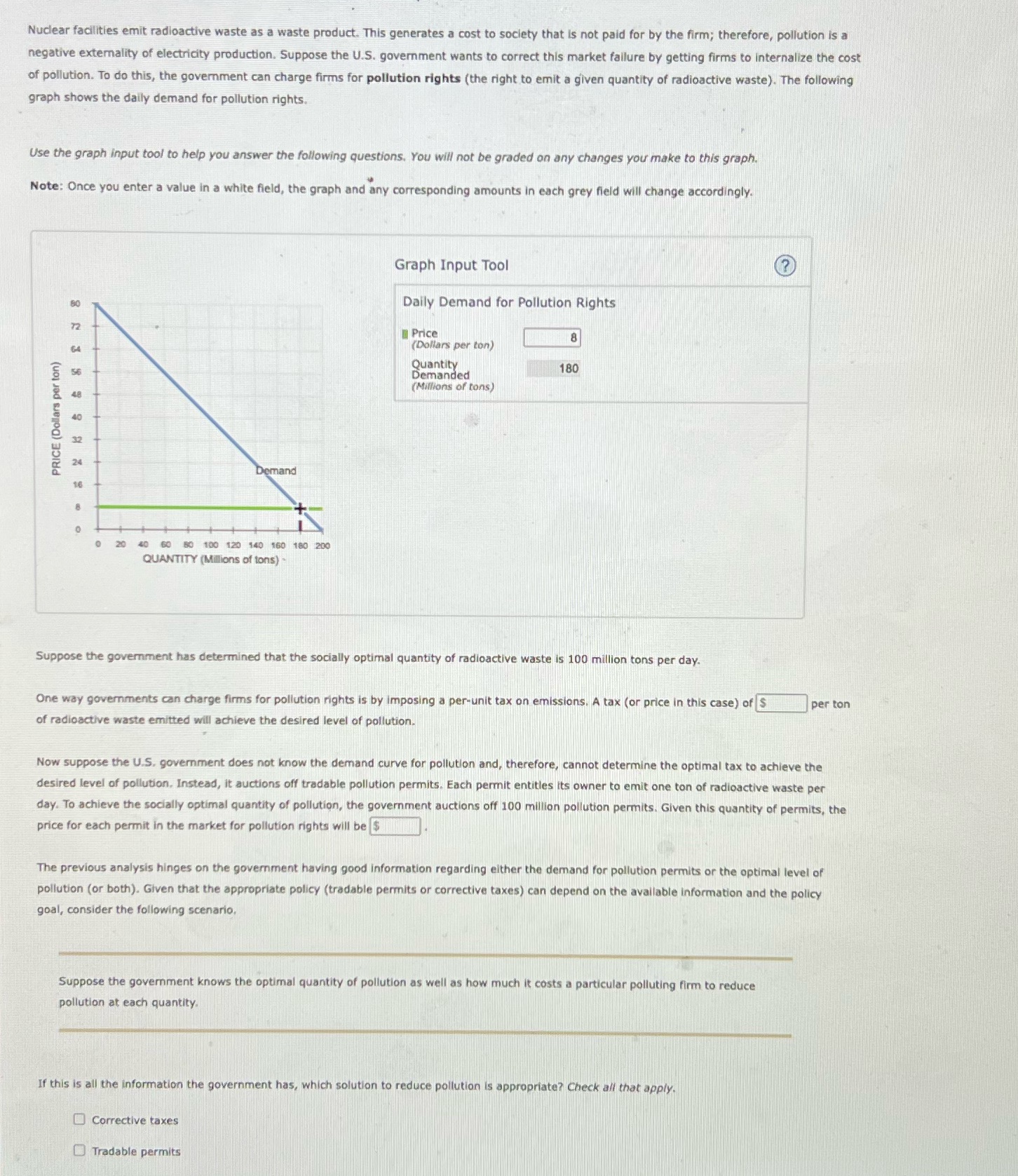
Nuclear facilities emit radioactive waste as a waste product. This generates a cost to society that is not paid for by the firm; therefore, pollution is a negative externality of electricity production. Suppose the U.S. government wants to correct this market failure by getting firms to internalize the cost of pollution. To do this, the government can charge firms for pollution rights (the right to emit a given quantity of radioactive waste). The following graph shows the daily demand for pollution rights. Use the graph input tool to help you answer the following questions. You will not be graded on any changes you make to this graph. Note: Once you enter a value in a white field, the graph and any corresponding amounts in each grey field will change accordingly. Graph Input Tool Daily Demand for Pollution Rights Price (Dollars per ton) Quantity 180 Demanded (Millions of tons) PRICE (Dollars per ton) 20 40 60 50 100 120 540 160 180 200 QUANTITY (Millions of tons) Suppose the government has determined that the socially optimal quantity of radioactive waste is 100 million tons per day. One way governments can charge firms for pollution rights is by imposing a per-unit tax on emissions. A tax (or price in this case) of $ per ton of radioactive waste emitted will achieve the desired level of pollution. Now suppose the U.S. government does not know the demand curve for pollution and, therefore, cannot determine the optimal tax to achieve the desired level of pollution. Instead, it auctions off tradable pollution permits. Each permit entitles its owner to emit one ton of radioactive waste per day. To achieve the socially optimal quantity of pollution, the government auctions off 100 million pollution permits. Given this quantity of permits, the price for each permit in the market for pollution rights will be $ The previous analysis hinges on the government having good information regarding either the demand for pollution permits or the optimal level of pollution (or both). Given that the appropriate policy (tradable permits or corrective taxes) can depend on the available information and the policy goal, consider the following scenario, Suppose the government knows the optimal quantity of pollution as well as how much it costs a particular polluting firm to reduce pollution at each quantity. If this is all the information the government has, which solution to reduce pollution is appropriate? Check all that apply. Corrective taxes Tradable permits