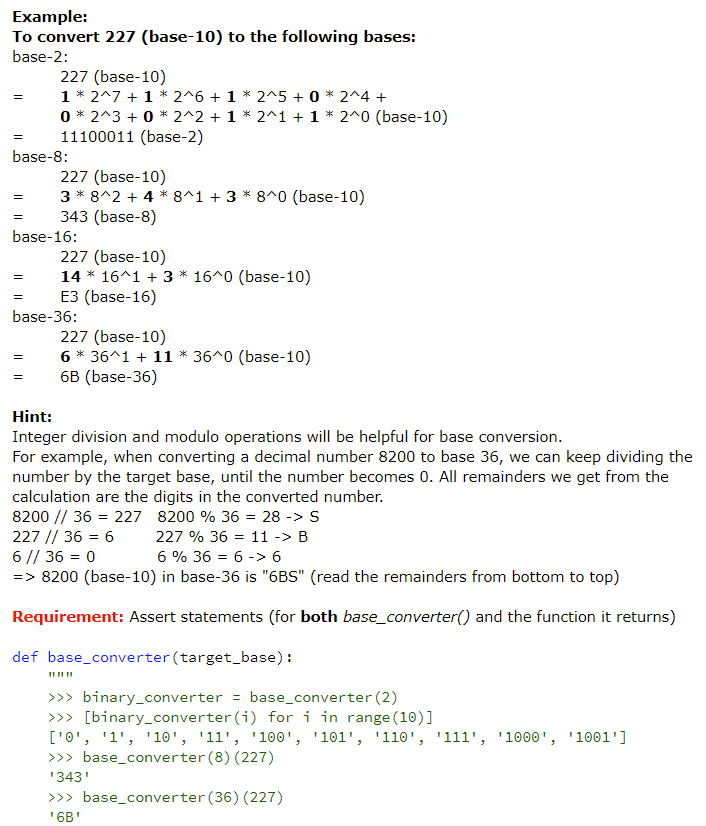
Number base conversion is an important concept in the Computer Science field. Since computers store the numbers as binary (using only 1s and Os), bases of the power of 2 are frequently used (especially base 2, 8 and 16) to represent the binary-encoded values. In addition, converting a number to a higher base can save space when the number is too large. For example, to convert the number 124 (base-10) to base-16, we do the following calculation: 124 = 7 * 16^1 + 12 * 1640 We represent 12 with the letter C (see the chart below), so now 124 (base-10) can be represented as "70" in base-16. We have saved one digit space here! When the base is greater than 10, we use letter A-Z to express digits with value 10-35, thus we can convert a number to at most base-36 with the numbers + alphabet notation. value o 1 8 9 10 11 33 35 12 34 digit 0 1 .. 8 9 . B ... X Y Z Write a function that generates a base converter function. This function takes a target base (integer between 2 and 36, both inclusive), and returns a function that takes a non-negative integer in decimal (base-10), and converts it to the target base as a string. * Example: To convert 227 (base-10) to the following bases: base-2: 227 (base-10) 1* 247 +1 * 246 + 1 * 25 + 0* 2^4 + 0* 2^3 + 0* 2^2 +1 * 2^1 +1 * 2^0 (base-10) 11100011 (base-2) base-8: 227 (base-10) 3* 8^2 + 4*8^1 + 3 * 8^0 (base-10) 343 (base-8) base-16: 227 (base-10) 14 * 16^1 + 3 * 16^0 (base-10) E3 (base-16) base-36: 227 (base-10) 6* 36^1 + 11 * 36^0 (base-10) 6B (base-36) = = = = = = Hint: Integer division and modulo operations will be helpful for base conversion. For example, when converting a decimal number 8200 to base 36, we can keep dividing the number by the target base, until the number becomes 0. All remainders we get from the calculation are the digits in the converted number. 8200 // 36 = 227 8200 % 36 = 28->S 227 // 36 = 6 227 % 36 = 11 -> B 6 // 36 = 0 6% 36 = 6 -> 6 => 8200 (base-10) in base-36 is "6BS" (read the remainders from bottom to top) Requirement: Assert statements (for both base_converter() and the function it returns) def base_converter (target_base): >>> binary_converter = base_converter (2) >>> [binary_converter (i) for i in range (10)] ['0', '1', '10', '11', '100', '101', '110', '111', '1000', '1001'] >>> base_converter (8) (227) 343 >>> base_converter (36) (227) "6B