[numerical analysis] Consider the one-dimensional, heat equation 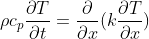, where rho is density, c_p heat capacity, k thermal conductivity, T temperature, x distance and t time.

If the thermal conductivity, density and heat capacity are constant over the model domain, the equation can be simplified to

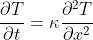where is the thermal diffusivity (a common value for rocks is ).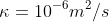

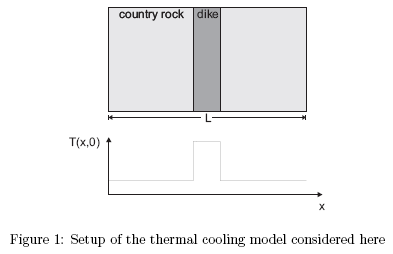
We are interested in the temperature evolution versus time, T(x,t), givene an initial temperature distribution Fig 1.

An example would be the intrusion of a basaltic dike in cooler country rocks.

The country rock has a temperature of 300(Celsius) and the dike a total width W = 5m, with a magma temperature of 1200(Celsius).

In addition we assume that the temperature far away from the dike center (at L/2 where L = 100m) remains at a constant temperature, 300(Celsius)

Let the 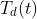be maximum temperature of dike when time is t.

Plot 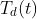graph by using natural cubic spline interpolation

Find the time t1 and 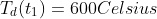by using bisection, Newton's method or secant method

Please use Matlab or Python

8? 8 , , ?? p?p ?t = ar * or 8? 8 , , ?? p?p ?t = ar * or