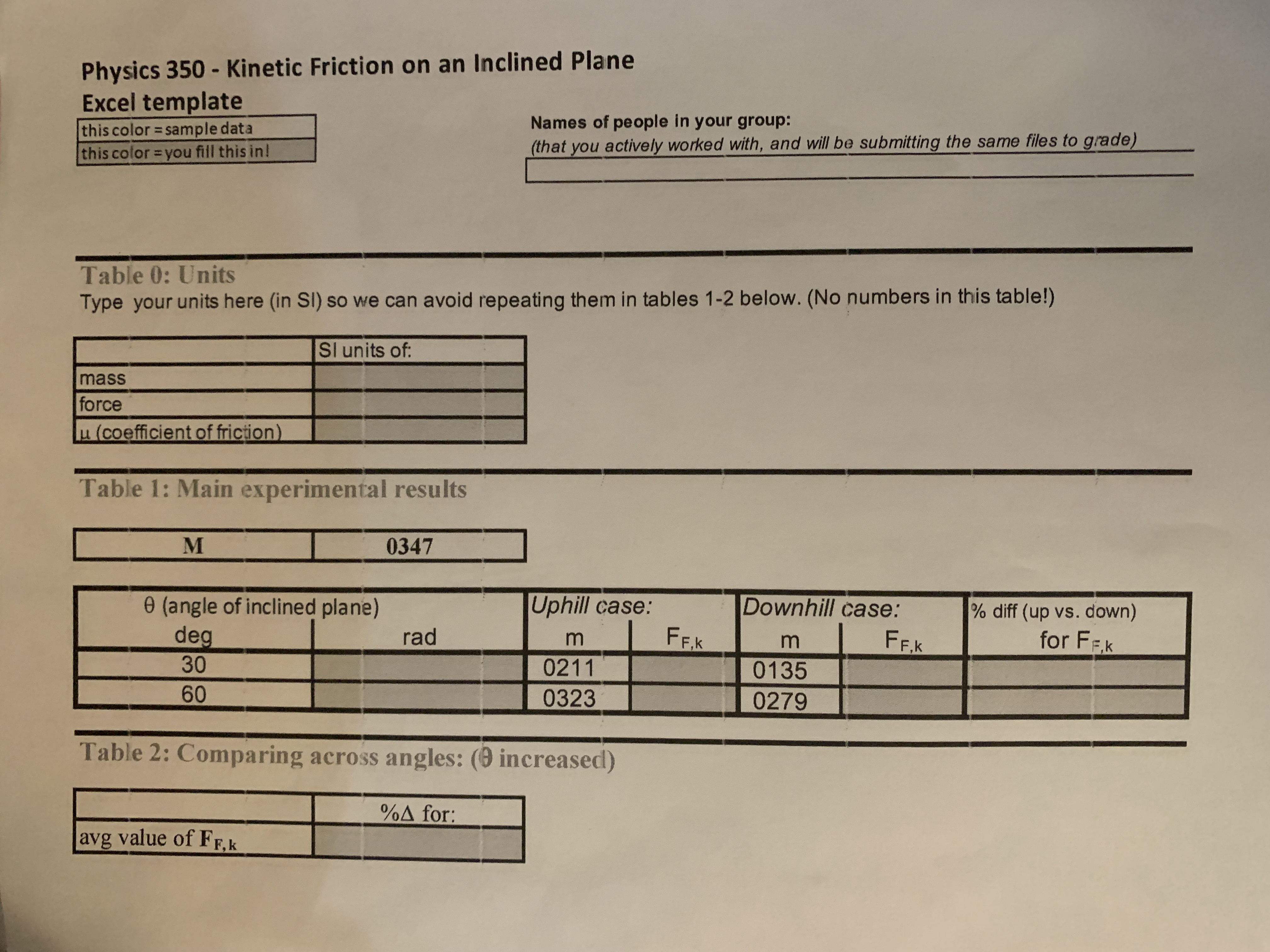
Objective: To explore the validity of the equation for the force of kinetic friction given in lecture, for a block sliding along an inclined plane at constant velocity. Theory: ecture, the size of the force of kinetic friction ( FF, ) on an object when sliding across a surface can be found with: FF,K = HK N (eqn 1) Where: HK = coefficient of kinetic friction (This is the characteristic "roughness" between the object and surface.) * const N = size of the normal force acting on object from surface (This measures the contact force between the object and surface.) M Also, by the simple application of Newton's Laws (see Final m Questions), without assuming eqn 1 is true, we can also infer the Size of the Frictional Force From context, in these cases. Uphill case: (block slides up incline at constant v) When block (M) slides at constant velocity up an incline, attached " const to a hanging mass (m), you can show that: FFK = mg - Mg sine (eqn 2) M Downhill case: (block slides down incline at constant v) m When the block (M) slides at constant velocity down the incline attached to a hanging mass (m), you can show that: Figure 1 FEK = Mg sino - mg (eqn 3) Assuming Newton's Laws are correct, we now have a way of finding the force of friction experimentally (eqns #2-3) and can compare those results with what eqn #1 predicts, to determine its validity. Procedure: Online lab: in this virtual version of the lab, you won't be able to gather your own data-but read along with these steps so that you can visualize the experiment, and understand how the data was collected. That will you put you in a position to understand how to analyze the provided sample data. 1. Measure and record the mass M of the block onto the Excel template for this lab (in table 1). This block will have a constant mass throughout this experiment. Please also take a moment to fill in table 0 (the units of today's quantities, so that you can dispense with units for the rest of the tables.) Online lab: the experimental value for M is already recorded for you. Z. Arrange the inclined plane, block, and hanging mass m (including hanger! ) as shown Fig I above, with an angle of incline of 0 = 30. (Note that the theoretical scenario assumes the string runs parallel to the incline, so make sure you adjust your pulley so this is also the case for your experimental apparatus.) 3. Uphill case: By experimentation, find the mass of the hanging mass (m) so that the system is able to undergo Lab #5: Kinetic Friction on an inclined plane - p. 6the motion in the uphill case shown in Figure I above. You should give the object a firm tap to start the motion, and then estimate whether the velocity is constant as best you can with the naked eye (if not, adjust m further.) Online lab: the experimental value for m (uphill case) is already recorded for you in Table 1. It might be surprising that you do not need a measurement device to be sure the system is moving at constant velocity, but the human eye is quite adept at noticing even small speed changes over a long enough slide. (I have also omitted several "tips" on how to best achieve good results, since they are not very informative if you are not performing this experiment in person.) 4. Downhill case: Repeat step #3, but now for the block moving down the incline (downhill case). This will require a different amount of hanging mass m. Online lab: the experimental value for m (downhill case) is already recorded for you in Table 1. 5. Now, adjust the angle of the inclined plane (see step 2) to 0 = 60 and repeat steps #13-4. Online lab: the experimental values for m (uphill & downhill cases) are already in Table 1. Analysis: 6. With your data for M, m, and A, use eans 2 and 3 to calculate FF,kin each case (uphill and downhill, and both angles). Make sure to do these computations in Excel. Things to keep in mind: - Excel is always in radians mode (see previous lab), so please convert your angles accordingly before using them in your computations, similarly to how you did so in your last lab (Projectile Motion, Part 1.) - Please remember the value of "g" is NOT negative. Feel free to include its numerical value directly in your formulas to expedite (or if you're comfortable: do it more properly, like your "c" value from Lab #1, Part 1.) - Fek is the SIZE of the force (always positive), so if it comes out negative, check your work! 7. Compute a % difference* in the friction force, uphill vs. downhill on the incline, for each angle, in table 1. (Now your table 1 should be filled in except for the rightmost three columns-we'll come back to those later.) *Basic Error Analysis is all we will use today. Please note there are several variants (% error, % difference, and % change), two of which you will use today-do not confuse them with each other. The details are on p. 2-3 of the Error Analysis reference document (see lab # 1 materials.) In tests I-III below, you will now examine whether the theoretical formula (eqn 1) seems valid, by comparing it against your experimental results from above. Test I: Direction of motion dependence Compare when block M is sliding uphill vs. sliding downhill the incline (at a given incline angle). Q1.) a.) According to theory, which of these should change between the two cases (uphill vs. downhill)? Select one choice for each (underline, change its color, etc), and include a brief explanation for each. Uk change? yes no N change? yes no FEK change? yes nob.) So then, according to theory, what would you ideally expect your % differences to be? Select one choice and include a brief explanation. zero non-zero c.) Experiment: Compare this against your experimental results, as best you can. In your answer, quote the relevant numerical results of your basic error analysis (on your spreadsheet.) 8.) Assuming your results came out reasonably close to theory, you should also see why it is reasonable to compute an average frictional force, by averaging the uphill and downhill cases at a given angle. Please perform this computation and record on table 1. This will give us a single average value for FEK to use at each angle; we can then find out what happens to that value looking across the two angles in tests II-III below. Test II: Normal force dependence 9.) Compute a percent change % (not % difference) in the average friction force, when the angle is increased from 0 = 30 to 0 = 60 , in table 2 on the Excel template. Q2.) a.) According to theory, which of these should change when the incline angle is increased? Select one choice and include a brief explanation for each. HK change? yes no N change? yes no FEK change? yes no b.) So then, according to theory, what would you ideally expect the % to be? Select one choice and include a brief explanation. zero non-zero c.) Experiment: Compare this against your experimental results, as best you can. In your answer, quote the relevant numerical result from your basic error analysis (from your sheet).Test III: Coefficient of friction dependence Investing eqn #1 to solve for jutt yields: HK = FF.K N (eqn la) Q3.) From your previous work with inclined planes (HW#4-5). what is the expression for the normal force (N) acting on the block? Express in terms of variables. Justify/show your work below. Be careful of which mass (m or M) is appropriate. 10.) Use your Q3 response to compute N at each angle (table 1). Then use these values and your average FF,k values (the average value of the uphill & downhill cases) with eqn #la, having Excel compute an experimental average uk value at each angle. Now your table 1 should be completed. 11.) Compute a %4 in the average uk value as the angle increases, and record onto table 2. Q4.) . Theory: (parts a-c) Should uk increase, decrease, or stay the same... a.) ... going uphill vs. going downhill on the incline, at a given angle? Explain. b.) ... when the angle of the incline increases from 0 = 30 to 0 = 60? Explain. C.) According to theory, what would you ideally expect the %A (from step #il) to be? Select one choice and include a brief explanation. zero non-zero d.) Experiment: Compare this against your experimental results, as best you can. In your answer, quote the relevant numerical result from your basic error analysis (from your sheet).Final Questions: Q5.) Wrap-up: Explain how each test (1, II & III) does its part to confirm the theoretical equation for kinetic friction (eqn 1.) Test 1: Test II: Test III: Q6.) Derive eqns #2-3 starting from Newton's Laws. Strongly recommended, though not required: to start with, catalog all forces on both objects by drawing them into Fig 1, for both the uphill & downhill cases. Think about what changes between the two cases. Hint: Since we are using constant velocity, this will make things much easier. If you do not have a more advanced/preferred method, you will probably want to write this computation on paper, take a photo, and then insert the image to this docx file (before saving it as a pdf). If the space provided here (including erasing this note) is not enough for you, feel free to write "see attached" here and include it as another page at the end. Q7.) Reflect back on your work for Q6. For the hanging mass (m), was the tension acting on it the same size as the force of gravity, in both cases (uphill and downhill)? If so, is this always true (in general), or just for the constant velocity cases we looked at today? Explain.Physics 350 - Kinetic Friction on an Inclined Plane Excel template this color = sample data Names of people in your group: this color = you fill this in! (that you actively worked with, and will be submitting the same files to grade) Table 0: Units Type your units here (in SI) so we can avoid repeating them in tables 1-2 below. (No numbers in this table!) SI units of: mass force u (coefficient of friction) Table 1: Main experimental results 0347 0 (angle of inclined plane) Uphill case: Downhill case: % diff (up vs. down) deg rad E FF.K E FF. K for FF, K 0211 0135 0323 0279 Table 2: Comparing across angles: (0 increased) % for: avg value of FF, k