Objective:

Work with graphs and Kruskals algorithm for minimum spanning trees.

Overview:

The pseudocode for Kruskals algorithm is given to find a minimum spanning tree of a graph. Your program will find the minimum spanning tree among a set of cities in Texas.

Details:

Write a command-line program that uses Kruskal's algorithm to find a minimum spanning tree of a graph. The graph will be provided as a file named assn9_data.csv. The data in the file is in the form of an adjacency list.

You must use the author's DisjSets class without modifying it. You can either use one of the author's priority queue classes or you can use the PriorityQueue class provided in Java.

You should output each edge of your minimum spanning tree as the names of the two cities and the distance between them. You should also print the sum of all of the distances in the tree.

Submit as: Kruskals.java

ArrayList kruskal( List edges, int numVertices ) { DisjSets ds = new DisjSets( numVertices ); PriorityQueue pq = new PriorityQueue( edges ); List mst = new ArrayList( ); while( mst.size( ) != numVertices - 1 ) { Edge e = pq.deleteMin( ); // Edge e = (u, v) SetType uset = ds.find( e.getu( ) ); SetType vset = ds.find( e.getv( ) ); if( uset != vset ) { // Accept the edge mst.add( e ); ds.union( uset, vset ); } } return mst; }

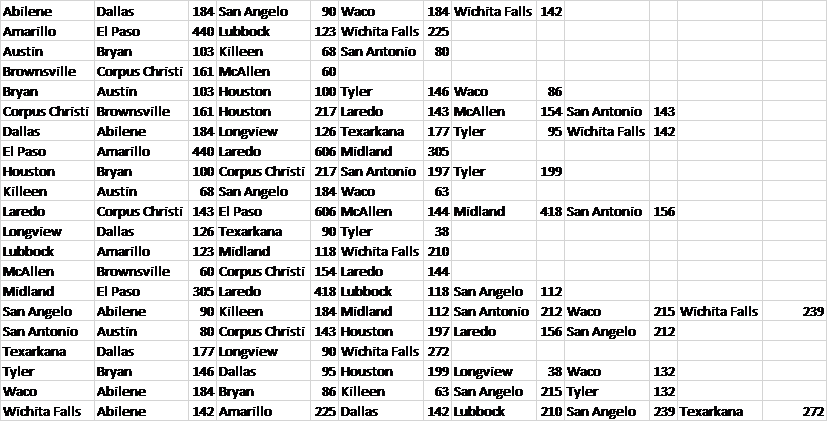
assn9_data.csv file: https://www.mediafire.com/file/e4jpii3k4bpuaye/assn9_data.csv

// DisjSets class // // CONSTRUCTION: with int representing initial number of sets // // ******************PUBLIC OPERATIONS********************* // void union( root1, root2 ) --> Merge two sets // int find( x ) --> Return set containing x // ******************ERRORS******************************** // No error checking is performed

/** * Disjoint set class, using union by rank and path compression. * Elements in the set are numbered starting at 0. * @author Mark Allen Weiss */ public class DisjSets { /** * Construct the disjoint sets object. * @param numElements the initial number of disjoint sets. */ public DisjSets( int numElements ) { s = new int [ numElements ]; for( int i = 0; i

/** * Union two disjoint sets using the height heuristic. * For simplicity, we assume root1 and root2 are distinct * and represent set names. * @param root1 the root of set 1. * @param root2 the root of set 2. */ public void union( int root1, int root2 ) { if( s[ root2 ]

/** * Perform a find with path compression. * Error checks omitted again for simplicity. * @param x the element being searched for. * @return the set containing x. */ public int find( int x ) { if( s[ x ]

private int [ ] s;

// Test main; all finds on same output line should be identical public static void main( String [ ] args ) { int NumElements = 128; int NumInSameSet = 16;

DisjSets ds = new DisjSets( NumElements ); int set1, set2;

for( int k = 1; k

for( int i = 0; i ArrayList Edge> kruska ( List Edge edges, int numVertices DisjSets ds = new DisJ Sets( nuert ices ); PriorityQueue pq new PriorityQueue( edges ); List mst - new ArrayList Edge e pq.deleteMin();/Edge e SetType uset ds.find( e.getu)) setType vset = ds. find( e.gety( ) ); =(u, v) if( uset != vset ) // Accept the edge mst.add e); ds.union uset, vset); return mst; Figure 9.60 Pseudocode for Kruskal's algorithm