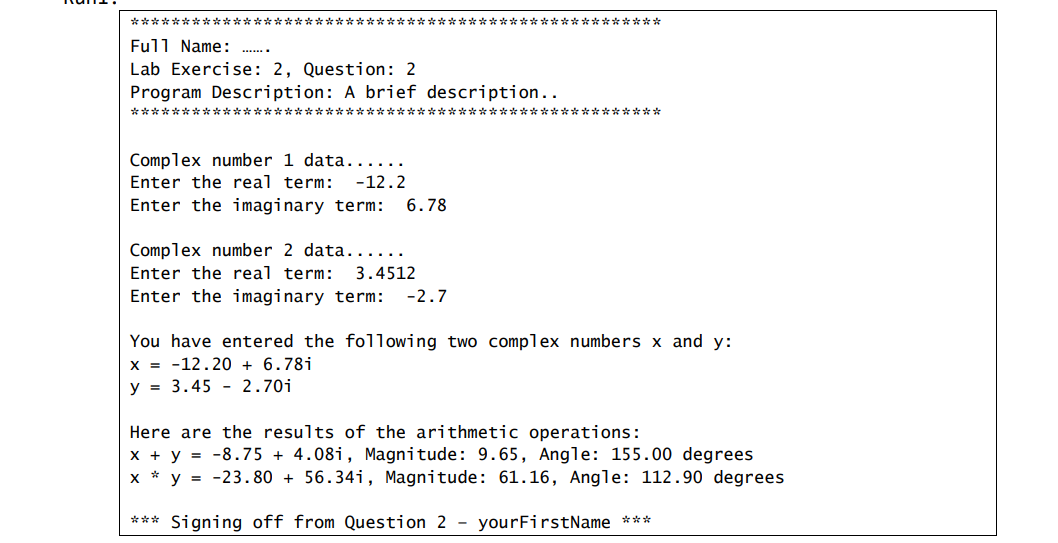
Objective: Write a program to perform arithmetic operations (addition and multiplication) on complex numbers. 1. Create a package called Q2. 2. Create a java class called ComplexNumber, as shown in the UML diagram. Specifications for the ComplexNumber Class: The constructor without argument will assign zero to all the field values. The constructor with parameter should accept the real and imaginary values as arguments and assign these values to the fields (real and imaginary). - Define the accessor/getter methods only; no mutator/setter methods are required. The getMagnitude() method is a helper method which will return the magnitude of a complex number. Magnitude of a complex number: a+bi=a2+b2 (Use Math.pow() and Math.sqrt() methods) - The getAngle( ) method is a helper method which will return the angle of a complex number in degrees. Angle of a complex number (a+bi) is tan1ab (Here, i is a symbol for the imaginary part of the number. For tan1ab use Java's Math class Math.atan2(b, a) that returns the angle in radians, and use Math.toDegrees(x) method to convert the radians to degrees. You can use these two in nested form. See Unit 2, Part 5. All the trigonometric methods in the Math class return the results in radians, and to get the result in degrees one must use Math.toDegree(x) method) - The displayRecForm() method will display the complex number as shown in the sample output. For example, if the complex number is (a+bi), it should display a + bi with the corresponding a and b values. The i in the display needs to be hard coded as a literal. The displayed result should use up to 2 decimal places. 3. In the same Java package, create a driver class with the name ComplexNumberDemoYourFirstName. Import the Q1.StudentGradesByYourFirstName class at the top so that you can use your myHeader() and myFooter() methods from that class in the same way, you did in your last lab. This class will contain two public static fields - a Scanner type instantiated field, and an int type field with an initial value 0 , and four public-static methods - dataEntry(), complexAdder(), complexMultiplier() and main(). a) Specifications for dataEntryo method: o The header: public static ComplexNumber dataEntryO - Once called, inside the method, it will increment the integer type field you declared and use it to keep the track of the number of Complex numbers as you see in the sample output that says complex number 1,2 etc. - Then it will prompt the user to enter the real and imaginary parts of a complex number and get those with the help of the Scanner type data field you already declared in this class. At this point, it will declare a ComplextNumber type reference variable and instantiate it with the above values. Finally, it will return the above instantiated reference variable back to the calling method. b) Specifications for comlexAdder() method: - The header: public static ComplexNumber complexAdder (ComplexNumber x, ComplexNumber y) - Once called, it will declare a ComplextNumber type reference variable and instantiate it with the added real-term values of x and y, and the added imaginary-term values of x and y. Note: If there are two complex numbers x= a+bi, and y=c+di, then, x+y=(a+c)+(b+d)i. Example: if there are two complex number x=5+2i and y=43i, then, x+y=(5+4)+(213)i=911. It will return the above instantiated reference variable back to the calling method. c) Specifications for comlexMultiplier( ) method: o The header: public static ComplexNumber complexMultiplier (ComplexNumber x, ComplexNumber y) - Once called, it will declare a ComplextNumber type reference variable and instantiate it with the appropriate values that result from the multiplication of x and y. Note: If there are two complex numbers x=a+bi, and y=c+di, then, xy=(ac bd)+(bc+ad)i - It will return the above instantiated reference variable back to the calling method. d) Specifications for the Driver Method: Call myHeaderO) in the same way as you did for Q2 in your previous lab. Declare a ComplexNumber type reference variables x. Call the dataEntry() method and assign the returned value to x declared above. Repeat the same procedure for a second ComplexNumber type reference variables y Display the two complex numbers using the a + bi form as shown in the sample output using the displayRecForm() method. Declare a 3rd complex reference variable called addRes. Call the complexAdder() method with the reference variables x and y as arguments, and then assign the returned value to addRes. Declare a 4th complex reference variable called mulRes. Call the complexMultiplier() method with the reference variables x and y as arguments, and then assign the returned value to mulRes. Using proper method calls and appropriate print statements, display the results as shown in the sample output. - Call the myFooter( method in the same way as you did for Q2 in your previous lab. See your instructor during office hours, if you have any question or concern. Fu11 Name: Lab Exercise: 2, Question: 2 Program Description: A brief description.. Complex number 1 data..... Enter the real term: 12.2 Enter the imaginary term: 6.78 Complex number 2 data...... Enter the real term: 3.4512 Enter the imaginary term: 2.7 You have entered the following two complex numbers x and y : x=12.20+6.78iy=3.452.70i Here are the results of the arithmetic operations: x+y=8.75+4.08i, Magnitude: 9.65, Angle: 155.00 degrees xy=23.80+56.34i, Magnitude: 61.16, Angle: 112.90 degrees