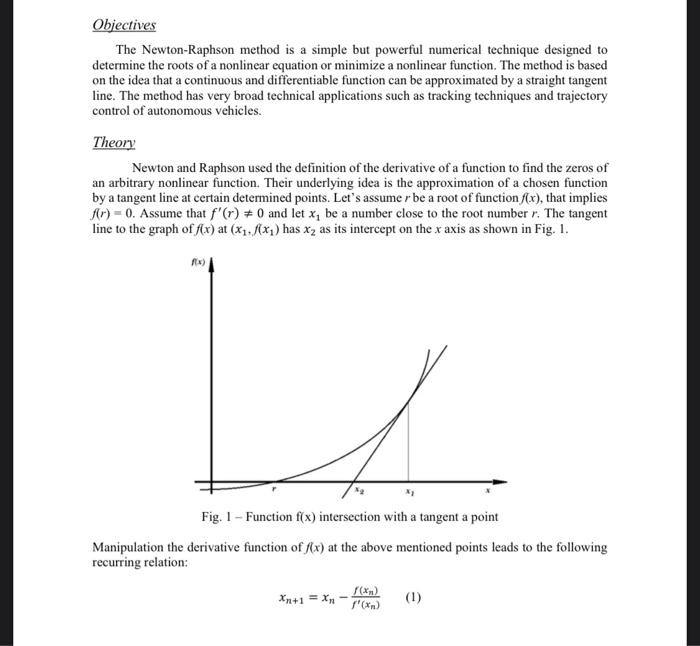
Objectives The Newton-Raphson method is a simple but powerful numerical technique designed to determine the roots of a nonlinear equation or minimize a nonlinear function. The method is based on the idea that a continuous and differentiable function can be approximated by a straight tangent line. The method has very broad technical applications such as tracking techniques and trajectory control of autonomous vehicles. Theory Newton and Raphson used the definition of the derivative of a function to find the zeros of an arbitrary nonlinear function. Their underlying idea is the approximation of a chosen function by a tangent line at certain determined points. Let's assumer be a root of function f(x), that implies kr) - 0. Assume that f'(r) = 0 and let xbe a number close to the root number r. The tangent line to the graph of f(x) at (x1, f(xi) has Xz as its intercept on the x axis as shown in Fig. 1. ) Fig. 1 - Function f(x) intersection with a tangent a point Manipulation the derivative function of f(x) at the above mentioned points leads to the following recurring relation: Xn+1 = x (1) 1'() Programming The goal of this lab is to design an iterative MATLAB program using a FOR loop to determine the roots of a series of given functions. To that end, the program should be able to calculate the derivatives of the given functions, substitute an initial value x, do the iteration using the FOR loop, plot the iterated roots approximations versus the number of iterations to verify the convergence of the Newton-Raphson scheme, and verify that the final approximated value is effectively the root of the function. 1. Task 1 Find the root of the function f(x) = x2 - 5. Determine the number of iterations realizing a convergence up to 20 digits. 2. Task 2 Find the root of the function f(x) = x - cos(x). Determine the number of iterations realizing a convergence up to 20 digits. 3. Task 3 Find the root of the function f(x) = x + 5x - 3. Determine the number of iterations realizing a convergence up to 20 digits. 4. Task 4 Approximate up to 20 decimals the number V3 using the Newton-Raphson scheme. Provide a digital copy of your script showing your MATLAB code. Explain your code step by step