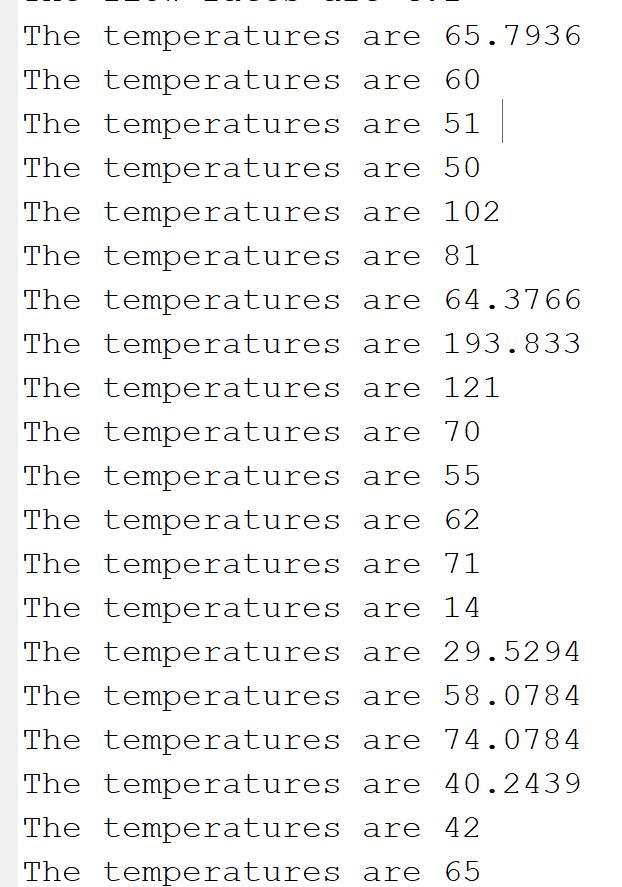
Objectives Using the information presented in the problem statement, you are to: 1. Solve the linear mass balances for all flow rates F...F- 2. Using the solution to the mass balances, solve the linear energy balances for T0. If the known temperatures are as reported in the problem statement. 3. Determine if the solution from (2) obeys the second law of thermodynamics as described in the problem statement. if all other given temperatures are unchanged, determine the maximum allowable temperature for Tu so that no laws of thermodynamics are broken anywhere in the HEN. Deliverables You are to submit a code package containing a driver code that outputs the following once the "play" button is pressed: 1. Display the flow rates FF in the command line (using fprintf() or table()). 2 Display the temperatures 7,720 in the command line (using fprintf() or table()). 3. Display in the command line if any streams violate the second law if T = 14C 4. Display in the command line the maximum allowable temperature for T to obey the second law. Advice You can solve the mass balances as a 20x20 system of equations in the form Ax - b. I suggest also solving the energy balances as a 2020 system of equations. . Remember, information like T = 14 can be treated as a parameter (thus removing one DOF by removing one variable), or as an equation (thus removing one DOF by adding one equation). For the second law, I suggest a series of if statements to test the inequalities. . There are four inequalities for each heat exchanger. . To find the critical temperature for T4, you will need at least one loop. With all of this in mind, we can perform complete mass and energy balances around all seven exchangers A-G. I'll get you started by giving you the balances for exchanger A: Mass Balances (in-out): Energy Balance (in out): F-F (hot stream balance) Fi-Fi (cold stream balance) Note that there are TWO mass balances for exchanger A since each stream (shown here as mass flow, F) is kept separate, but ONE energy balance because thermal energy (shown here as enthalpy, H) is transferred from one stream to the other. Assuming no phase changes, constant heat capacities, and no losses to the environment (all listed above), the enthalpy of some stream i is defined as H, and has the following relationship that you probably remember from grade 11 chemistry: H = F,CpT Where T, is the temperature of stream i in [K] and Cp, is the heat capacity of stream i in [kJ/kg-K]. You have the following table of data from your most recent plant samples: Table 1: Stream table for HEN in Figure 1 Flow F Stream Heat Capacity Cpi (kg/sec) (kJ/kg-K) 1 3.3 24 5 24 26 8 1.8 0.8 11 6.9 0.95 14 3.4 1.35 18 41 1.1 You have a set of KNOWN stream temperatures that are required in the plant, and other temperatures you DO NOT KNOW but need to be calculated based on the energy balances: T = 77C T-60C TE=81C T3 - 51C Ta-77C T11=55C T-??C T12 = 62C T17-??C T = 71C Tia-77C T-50C T9=121C T14=14C T19-42C Ts-102C T10 = 70C T15 = ??"C Tao-65C You may want to note that there are seven missing temperatures, and you should be able to perform seven independent energy balances on exchangers A - G Finally, when assessing the feasibility of this design, the resulting temperatures must obey the second law of thermodynamics. In our case, this means the following two rules must hold: In any exchanger, the hot stream gets colder, and the cold stream gets hotter. (Example: T 7;) The streams cannot reach temperature crossover. That means that for a given exchanger A cold stream can never be heated until it is hotter than the hot stream inlet (Example: 7,7) A hot stream can never be cooled until it is colder than the cold stream inlet. (Example: T, T) With this in mind, we can complete our task to help design this HEN! Problem Statement You are a process engineer working for Syncrudd (an oil refiner) as they attempt to improve the energy efficiency of their Fort MacMurray cracker plant. For those of you that are interested, a "cracking" plant breaks down long-chained hydrocarbons (such as tars and heavy diesels) into shorter-chained hydrocarbons that can be blended into higher-value products such as gasoline, jet fuel, etc. Your lead engineer on the job has come up with a heat exchanger network (HEN) design that she knows will save the company utility costs in the long run (probably by using economic skills learned in ChE 4N04 or ENG 3PX3). She knows that it will work in principle, but just needs some expected stream temperatures to be calculated to ensure the network is thermodynamically attainable. The HEN transfers energy (heat) between three hot streams and three cold streams (we don't really care what they are made of) in the arrangement shown in Figure 1. Hot 1 Hot 2 Hot 3 F F F Fi Fyr Fia Cold 1- A F Fis Cold 2- Fis FI E Fi Fo F Cold 3 G Fr Figure 1: HEN proposed by your lead engineer. Hot streams are red and cold are blue. Stream numbers and exchanger letters are also shown. Note that the bubble with a squiggle is a standard chemical engineering icon for at heat exchanger... More details on heat exchangers can be found here. To analyze this system, we need to make a few assumptions: This system is being designed to operate at steady state. Therefore, the fluids are entering and leaving each exchanger at the same rate. The heat capacities of the hot and cold streams are constant and therefore do not change with temperature (not true generally, but good enough for now). All streams only exist in the one phase. All exchangers use the counter-current flow configuration, meaning the two streams flow in opposite directions. Therefore, the inlet for a cold stream enters at the same point as the outlet for a hot stream, and vice-versa. All exchangers are adiabatic (well insulated; no energy loss to environment). IMPORTANT: Heat exchangers do not mix streams. Therefore, whatever fluid enters as "hot" leaves as "hot" The same thing happens for "cold." See the sample balances below for an example. There are no pressure drops or any other realistic but annoying natural occurrences The temperatures are 65.7936 The temperatures are 60 The temperatures are 51 The temperatures are 50 The temperatures are 102 The temperatures are 81 The temperatures are 64.3766 The temperatures are 193.833 The temperatures are 121 The temperatures are 70 The temperatures are 55 The temperatures are 62 The temperatures are 71 The temperatures are 14 The temperatures are 29.5294 The temperatures are 58.0784 The temperatures are 74.0784 The temperatures are 40.2439 The temperatures are 42 The temperatures are 65