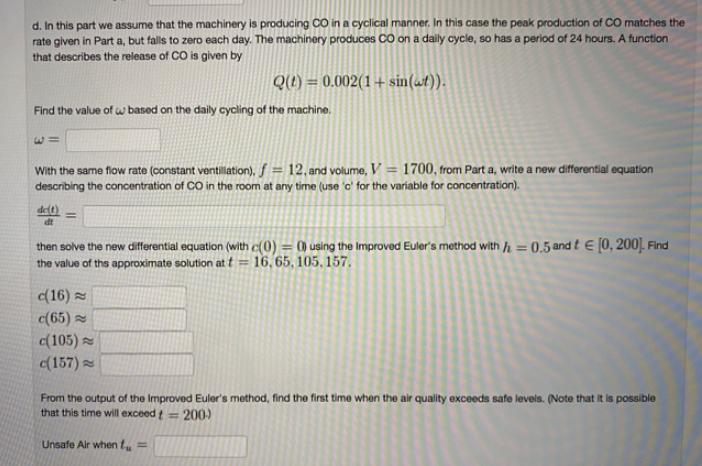
One important issue in environmental health is being able to maintain air quality in workplaces. It has been been shown that extended exposure to carbon monoxide as low as 0.00012 can be harmful. a. Consider a room with a volume, V = 1700 m, containing machinery that produces carbon monoxide (CO) at a rate Q(t)= 0.004 m/hr. Assume that ventillation brings fresh air into the room (assume constant volume and constant pressure) where it mixes completely, then exhausts at a rate of f 12 m/hr. If c(t) is the concentration of CO in the room at any time, then the differential equation describing this situation is given by (use c for the variable for concentration). P de(1) If the room is initially free of CO, so c(0) = 0. then solve this differential equation. c(t) = Find how long it takes until the air becomes unhealthy (exceeds 0.00012). Air Unhealthy when t = Eventually (limit as t tends to infinity), what will be the level of CO in this room? Limiting concentration= b. In your written HW, graph the solution for 48 hours. Briefly describe how you created the differential equation for this model and the techniques used to solve this linear differential equation. Include a description of the solution that you found. c. The equilibrium concentration in the room is found by setting the right hand side of the differential equation equal to zero. Assuming that Q(t) and V are fixed at the levels in Part a, then find the minimum flow rate of fresh air fe such that the equilibrium concentration is 0.00012. Critical flow rate fe d. In this part we assume that the machinery is producing CO in a cyclical manner. In this case the peak production of CO matches the rate given in Part a, but falls to zero each day. The machinery produces CO on a daily cycle, so has a period of 24 hours. A function that describes the release of CO is given by Find the value of w based on the daily cycling of the machine. W= With the same flow rate (constant ventilation), f = 12, and volume, V = 1700, from Part a, write a new differential equation describing the concentration of CO in the room at any time (use c for the variable for concentration). de(t) Q(t)= 0.002(1+ sin(t)). then solve the new differential equation (with c(0) = 0) using the Improved Euler s method with h = 0.5 and t [0, 200]. Find the value of the approximate solution at t 16,65, 105, 157. c(16) c(65) c(105) c(157) From the output of the Improved Euler s method, find the first time when the air quality exceeds safe levels. (Note that it is possible that this time will exceed t = 200) Unsafe Air when f =