Only C++

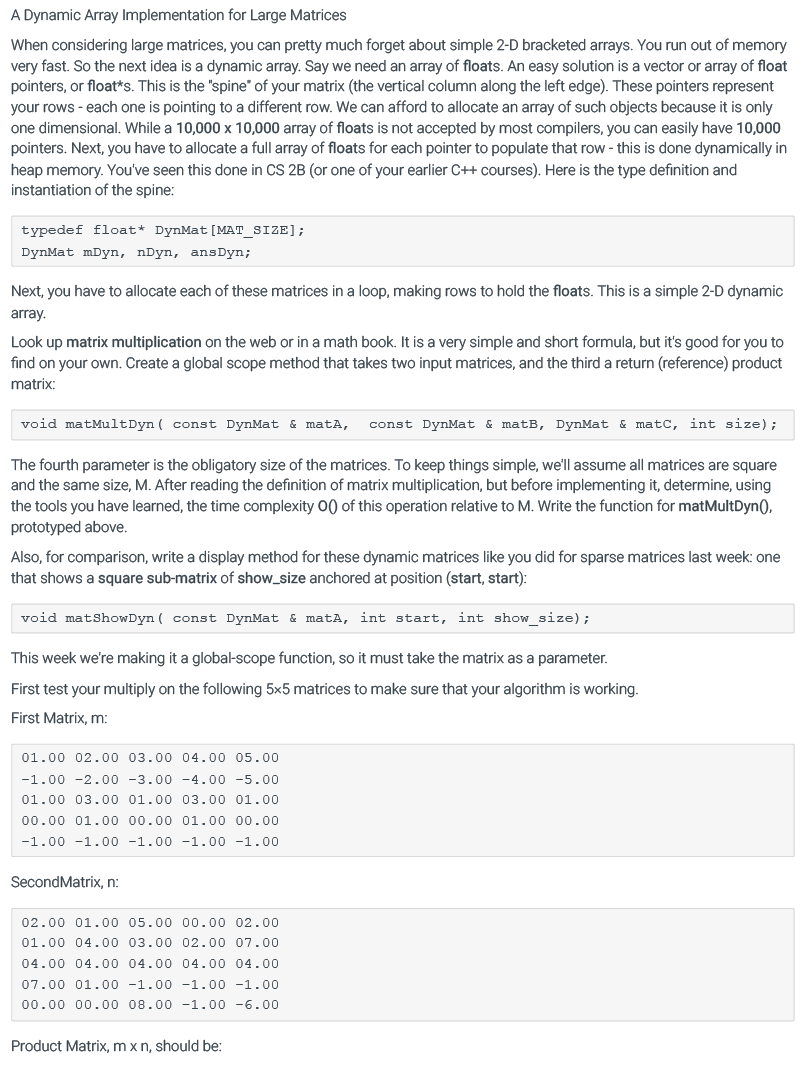
Please edit the below main.cpp by adding code to the areas that stated "code added by student"

// Assignment #3 Timing Matrix Multiplication (Part A) // CLIENT

#include #include using namespace std; #include

// --------------- main --------------- #define MIN_MAT_SIZE 1 #define MIN_PERCENT 1 #define MAX_PERCENT 10.0

// for matrix of fixed sizes #define MAT_SIZE 5 typedef float* DynMat[MAT_SIZE]; void matMultDyn(const DynMat & matA, const DynMat & matB, DynMat & matC, int size); void matShowDyn(const DynMat & matA, int start, int show_size);

// for Sparse Matrix of dynamically allocated sizes void matMultDynSp(float **matA, float **matB, float **matC, int size); void matShowDynSp(float **matA, int mat_size, int start, int show_size);

int main() { int r, c, mat_size; clock_t startTime, stopTime; double randFrac; int randRow, randCol, numElement; float smallPercent; // easy initialization, but only for fixed-size matrices float m[MAT_SIZE][MAT_SIZE] = {{1, 2, 3, 4, 5}, {-1, -2, -3, -4, -5}, {1, 3, 1, 3, 1}, {0, 1, 0, 1, 0}, {-1, -1, -1, -1, -1}};

float n[MAT_SIZE][MAT_SIZE] = {{2, 1, 5, 0, 2}, {1, 4, 3, 2, 7}, {4, 4, 4, 4, 4}, {7, 1, -1, -1, -1}, {0, 0, 8, -1, -6}};

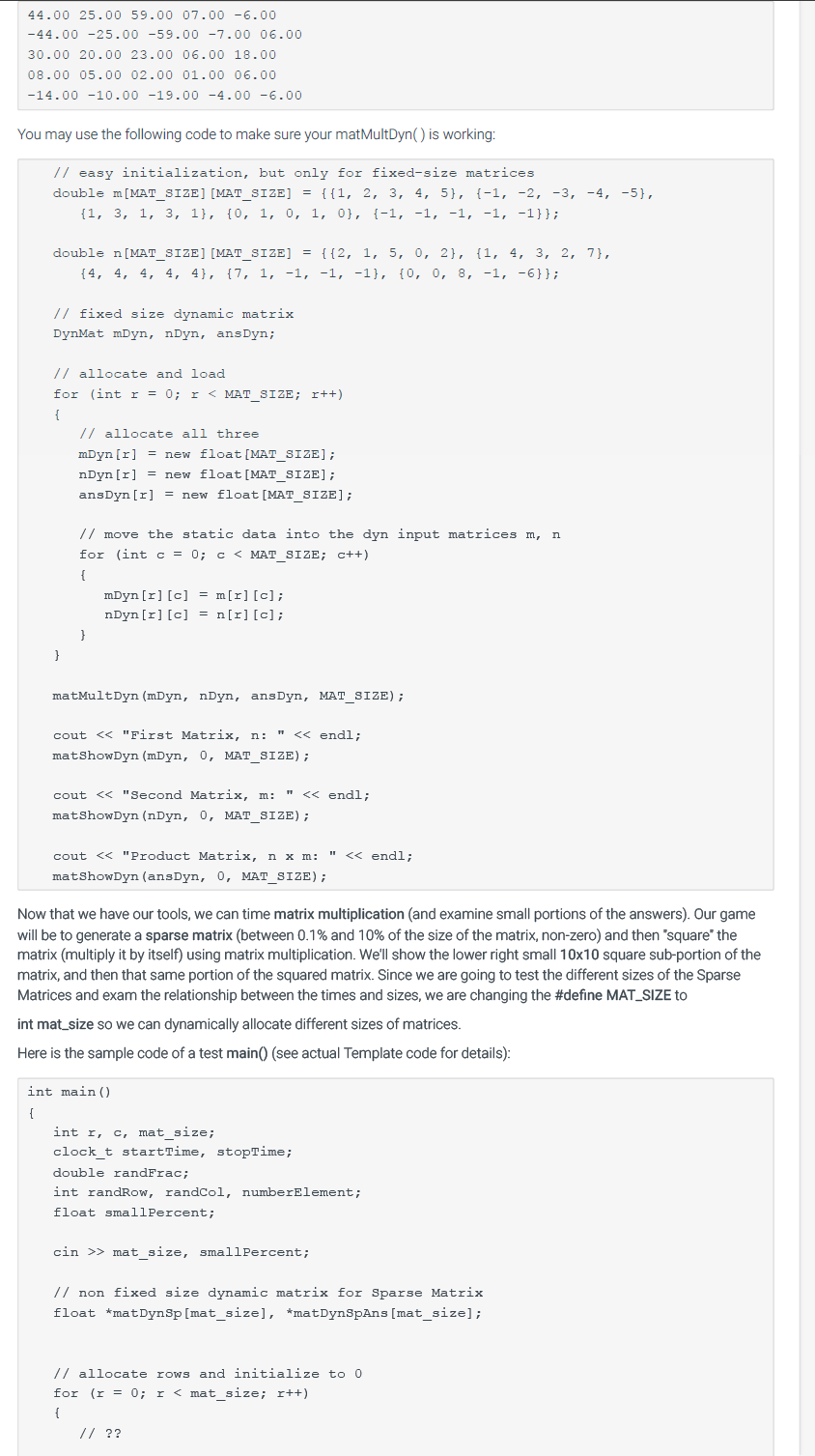
// for non-sparse dynamic matrix of fixed size DynMat mDyn, nDyn, ansDyn;

// allocate and load for (r = 0; r

// move the static data into the dyn input matrices m, n for (c = 0; c

matMultDyn(mDyn, nDyn, ansDyn, MAT_SIZE);

cout

cout

cout

// clean up for (r = 0; r > mat_size >> smallPercent; //check the input values and reset to MIN or MAX if out of range // code provided by student // // // non fixed size dynamic matrix float *matDynSp[mat_size], *matDynSpAns[mat_size];

// allocate rows and initialize to 0 for (r = 0; r

// initialize random seed to a fixed start 0 // so it will generate the same random sequence checked by the Auto Grader srand (0); // generate small % (between .1 and 10.) non-default values (between 0 and 1.0) numElement = mat_size * mat_size * smallPercent / 100; for (r = 0; r

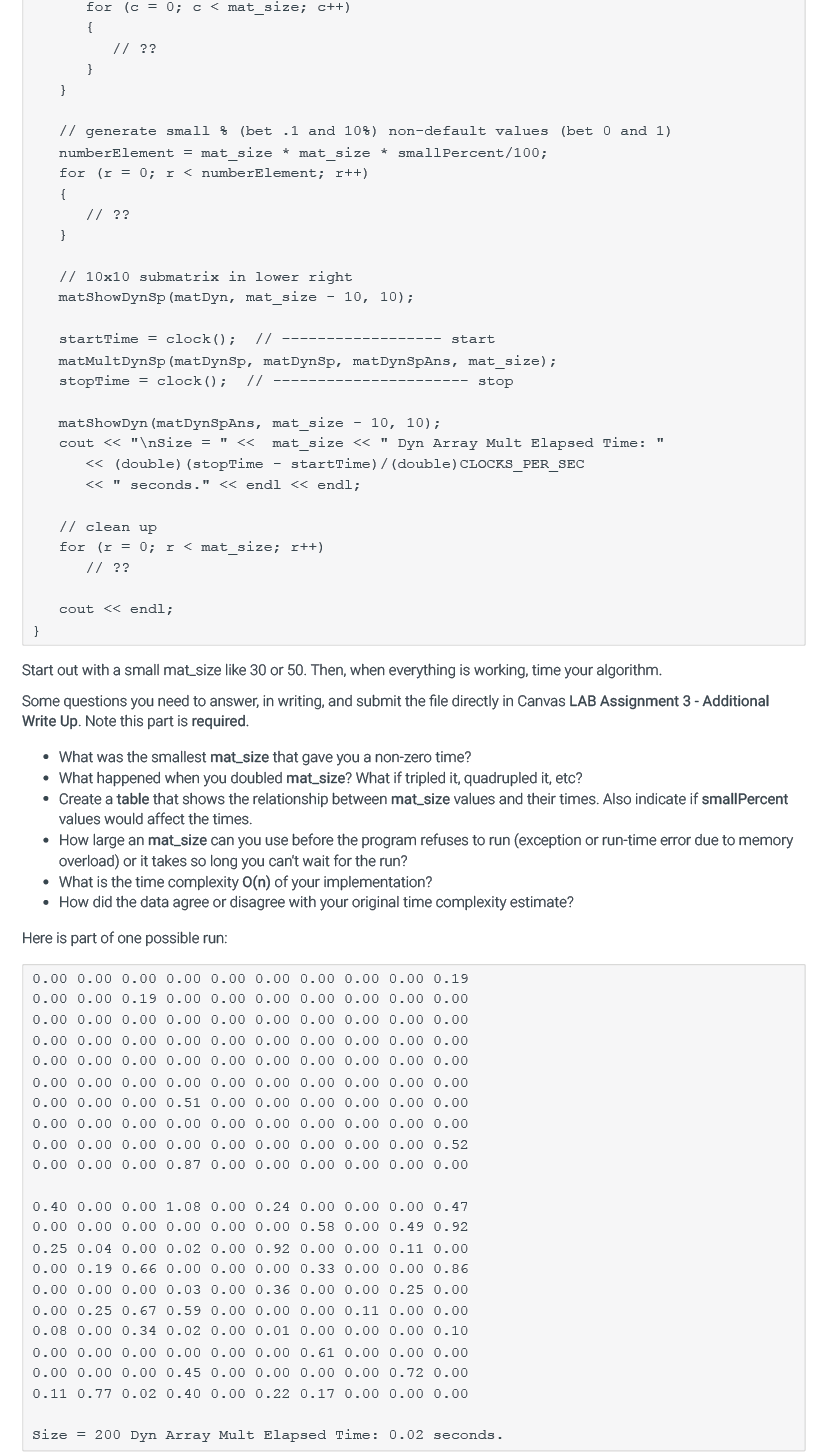
matShowDynSp(matDynSp, mat_size, mat_size - 10, 10);

startTime = clock(); // ------------------ start matMultDynSp(matDynSp, matDynSp, matDynSpAns, mat_size); stopTime = clock(); // ---------------------- stop

matShowDynSp(matDynSpAns, mat_size, mat_size - 10, 10);

cout

// clean up for (r = 0; r

void matMultDyn(const DynMat & matA, const DynMat & matB, DynMat & matC, int size) { // code provided by student // //

}

void matShowDyn(const DynMat & matA, int start, int show_size) { int r, c;

// code provided by student // // cout

void matShowDynSp(float **matA, int mat_size, int start, int show_size) { int r, c; // check the display range and make sure only data within the matrix will be shown // code provided by student // //

cout.width(6); cout.precision(2); cout

After writing main.cpp, please answer the following questions

• What was the smallest mat_size that gave you a non-zero time?
• What happened when you doubled mat_size? What if tripled it, quadrupled it, etc?
• Create a table that shows the relationship between mat_size values and their times. Also indicate if smallPercent values would affect the times.
• How large an mat_size can you use before the program refuses to run (exception or run-time error due to memory overload) or it takes so long you can't wait for the run?
• What is the time complexity O(n) of your implementation?
• How did the data agree or disagree with your original time complexity estimate?

A Dynamic Array Implementation for Large Matrices When considering large matrices, you can pretty much forget about simple 2-D bracketed arrays. You run out of memory very fast. So the next idea is a dynamic array. Say we need an array of floats. An easy solution is a vector or array of float pointers, or float*s. This is the "spine of your matrix (the vertical column along the left edge). These pointers represent your rows - each one is pointing to a different row. We can afford to allocate an array of such objects because it is only one dimensional. While a 10,000 x 10,000 array of floats is not accepted by most compilers, you can easily have 10,000 pointers. Next, you have to allocate a full array of floats for each pointer to populate that row - this is done dynamically in heap memory. You've seen this done in CS 2B (or one of your earlier C++ courses). Here is the type definition and instantiation of the spine: typedef float* DynMat[MAT_SIZE]; DynMat mDyn, nDyn, ansDyn; Next, you have to allocate each of these matrices in a loop, making rows to hold the floats. This is a simple 2-D dynamic array. Look up matrix multiplication on the web or in a math book. It is a very simple and short formula, but it's good for you to find on your own. Create a global scope method that takes two input matrices, and the third a return (reference) product matrix: void matMultDyn( const DynMat & mata, const DynMat & mats, DynMat & matc, int size); The fourth parameter is the obligatory size of the matrices. To keep things simple, we'll assume all matrices are square and the same size, M. After reading the definition of matrix multiplication, but before implementing it, determine, using the tools you have learned the time complexity 00 of this operation relative to M. Write the function for matMultDyn(), prototyped above. Also, for comparison, write a display method for these dynamic matrices like you did for sparse matrices last week: one that shows a square sub-matrix of show_size anchored at position (start, start): void matShowDyn( const DynMat & mata, int start, int show_size); This week we're making it a global-scope function, so it must take the matrix as a parameter. First test your multiply on the following 5x5 matrices to make sure that your algorithm is working. First Matrix, m: 01.00 02.00 03.00 04.00 05.00 -1.00 -2.00 -3.00 -4.00 -5.00 01.00 03.00 01.00 03.00 01.00 00.00 01.00 00.00 01.00 00.00 -1.00 -1.00 -1.00 -1.00 -1.00 Second Matrix, n: 02.00 01.00 05.00 00.00 02.00 01.00 04.00 03.00 02.00 07.00 04.00 04.00 04.00 04.00 04.00 07.00 01.00 -1.00 -1.00 -1.00 00.00 00.00 08.00 -1.00 -6.00 Product Matrix, mxn, should be: 44.00 25.00 59.00 07.00 -6.00 -44.00 -25.00 -59.00 -7.00 06.00 30.00 20.00 23.00 06.00 18.00 08.00 05.00 02.00 01.00 06.00 -14.00 -10.00 -19.00 -4.00 -6.00 You may use the following code to make sure your matMultDyn() is working: // easy initialization, but only for fixed-size matrices double m[MAT_SIZE] (MAT_SIZE] = {{1, 2, 3, 4, 5}, {-1, -2, -3, -4, -5}, {1, 3, 1, 3, 1}, {0, 1, 0, 1, 0}, {-1, -1, -1, -1, -1}}; double n[MAT_SIZE] [MAT_SIZE] = {{2, 1, 5, 0, 2}, {1, 4, 3, 2, 7}, {4, 4, 4, 4, 4}, {7, 1, -1, -1, -1}, {0, 0, 8, -1, -6}}; // fixed size dynamic matrix DynMat mDyn, nDyn, ansDyn; // allocate and load for (int r = 0; r > mat_size, smallPercent; // non fixed size dynamic matrix for Sparse Matrix float *matDynSp[mat_size], *matDynSpAns[mat_size]; // allocate rows and initialize to o for (r = 0; I