Only C++

Please edit the below main.cpp to get the same output as the example run.

#include

using namespace std;

#include #include #include #include

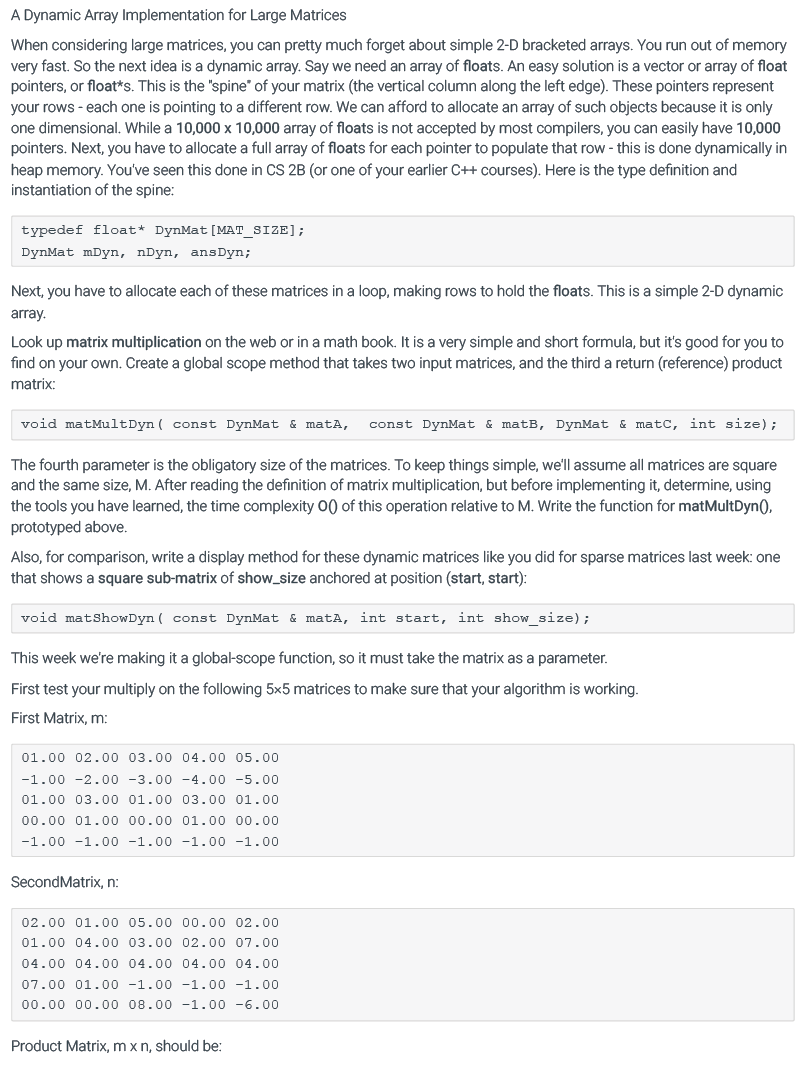
const int MAT_SIZE = 200; typedef float* DynMat[MAT_SIZE];

DynMat mDyn, nDyn, ansDyn;

// Create a global scope method that takes two input matrices, and the third a return (reference) product matrix: void matMultDyn( const DynMat & matA, const DynMat & matB, DynMat & matC, int size);

// display method for these dynamic matrices like you did for sparse matrices last week: one that shows a square sub-matrix of size = size anchored at position (start, start): void matShowDyn( const DynMat & matA, int start, int size);

// timing algorithms clock_t startClock() { return clock(); }

int main() { int r, c; clock_t startTime, stopTime; double randFrac; int randRow, randCol, smallPercent;

srand(time(0)); random_device rd; uniform_real_distribution dist(0, 1);

// format for cout cout

// non-sparse dynamic matrix DynMat matDyn, matDynAns;

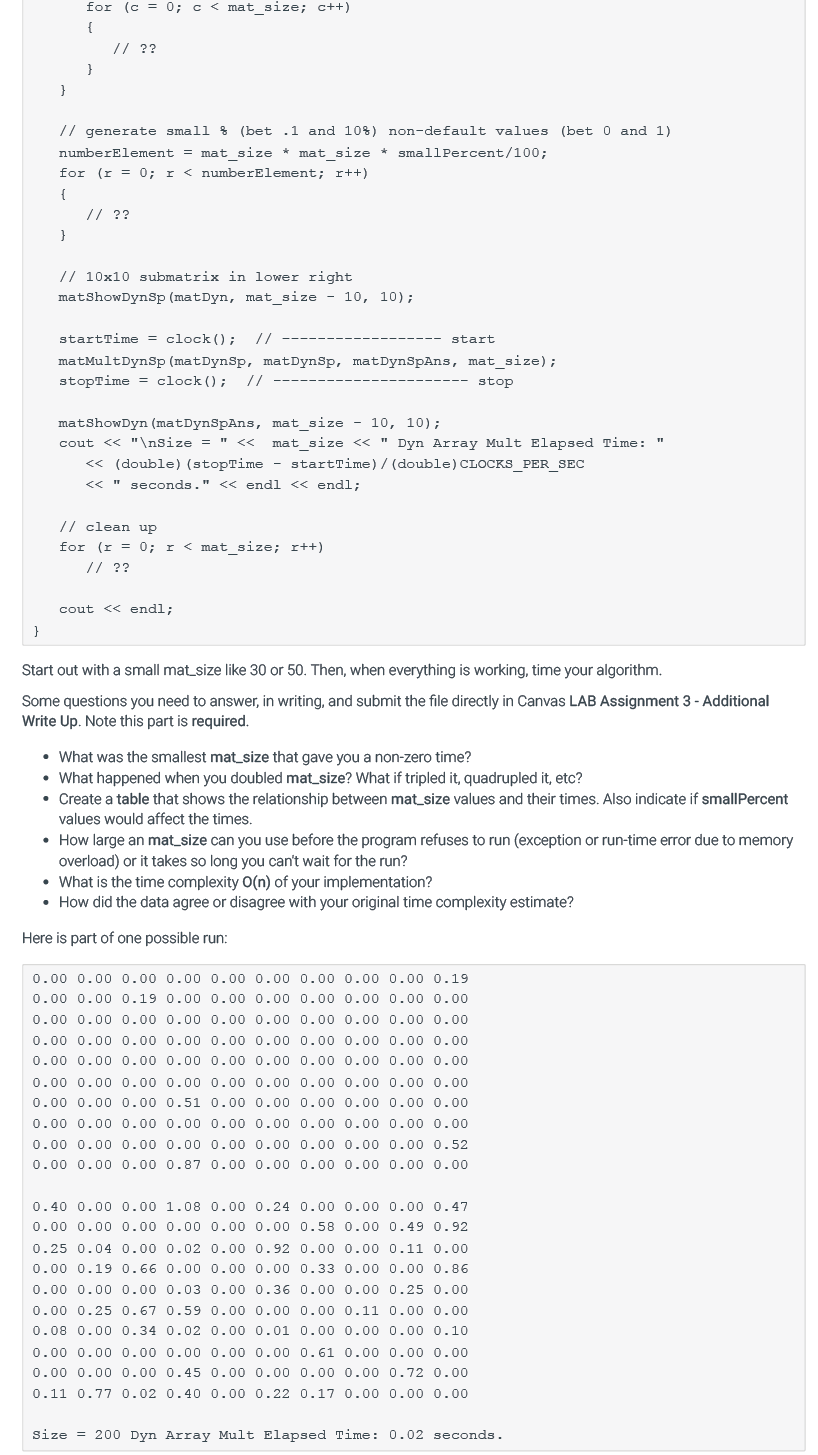
// allocate rows and initialize to 0 for (r = 0; r

// generate small% (bet .1 and 10%) non-default values (bet 0 and 1) smallPercent = MAT_SIZE/20. * MAT_SIZE; // div by 20. means 5%, of course for (r = 0; r

// 10x10 submatrix in lower right matShowDyn(matDyn, MAT_SIZE - 10, 10);

startTime = clock(); // ------------------ start matMultDyn(matDyn, matDyn, matDynAns, MAT_SIZE); stopTime = clock(); // ---------------------- stop

cout

// clean up for (r = 0; r

cout

void matShowDyn( const DynMat & matA, int start, int size) { for (int i = start; i

void matMultDyn( const DynMat & matA, const DynMat & matB, DynMat & matC, int size) { for (int r = 0; r

After writing main.cpp file, please answer the following questions

• What was the smallest M that gave you a non-zero time?
• What happened when you doubled M , tripled it, quadrupled it, etc? Create a table that shows the relationship between M values and their times.
• How large an M can you use before the program refuses to run (exception or run-time error due to memory overload) or it takes so long you can't wait for the run?
• What is the time complexity O(n) based on your analysis?
• How did the data agree or disagree with your original time complexity estimate?

A Dynamic Array Implementation for Large Matrices When considering large matrices, you can pretty much forget about simple 2-D bracketed arrays. You run out of memory very fast. So the next idea is a dynamic array. Say we need an array of floats. An easy solution is a vector or array of float pointers, or float*s. This is the "spine of your matrix (the vertical column along the left edge). These pointers represent your rows - each one is pointing to a different row. We can afford to allocate an array of such objects because it is only one dimensional. While a 10,000 x 10,000 array of floats is not accepted by most compilers, you can easily have 10,000 pointers. Next, you have to allocate a full array of floats for each pointer to populate that row - this is done dynamically in heap memory. You've seen this done in CS 2B (or one of your earlier C++ courses). Here is the type definition and instantiation of the spine: typedef float* DynMat[MAT_SIZE]; DynMat mDyn, nDyn, ansDyn; Next, you have to allocate each of these matrices in a loop, making rows to hold the floats. This is a simple 2-D dynamic array. Look up matrix multiplication on the web or in a math book. It is a very simple and short formula, but it's good for you to find on your own. Create a global scope method that takes two input matrices, and the third a return (reference) product matrix: void matMultDyn( const DynMat & mata, const DynMat & mats, DynMat & matc, int size); The fourth parameter is the obligatory size of the matrices. To keep things simple, we'll assume all matrices are square and the same size, M. After reading the definition of matrix multiplication, but before implementing it, determine, using the tools you have learned the time complexity 00 of this operation relative to M. Write the function for matMultDyn(), prototyped above. Also, for comparison, write a display method for these dynamic matrices like you did for sparse matrices last week: one that shows a square sub-matrix of show_size anchored at position (start, start): void matShowDyn( const DynMat & mata, int start, int show_size); This week we're making it a global-scope function, so it must take the matrix as a parameter. First test your multiply on the following 5x5 matrices to make sure that your algorithm is working. First Matrix, m: 01.00 02.00 03.00 04.00 05.00 -1.00 -2.00 -3.00 -4.00 -5.00 01.00 03.00 01.00 03.00 01.00 00.00 01.00 00.00 01.00 00.00 -1.00 -1.00 -1.00 -1.00 -1.00 Second Matrix, n: 02.00 01.00 05.00 00.00 02.00 01.00 04.00 03.00 02.00 07.00 04.00 04.00 04.00 04.00 04.00 07.00 01.00 -1.00 -1.00 -1.00 00.00 00.00 08.00 -1.00 -6.00 Product Matrix, mxn, should be: 44.00 25.00 59.00 07.00 -6.00 -44.00 -25.00 -59.00 -7.00 06.00 30.00 20.00 23.00 06.00 18.00 08.00 05.00 02.00 01.00 06.00 -14.00 -10.00 -19.00 -4.00 -6.00 You may use the following code to make sure your matMultDyn() is working: // easy initialization, but only for fixed-size matrices double m[MAT_SIZE] (MAT_SIZE] = {{1, 2, 3, 4, 5}, {-1, -2, -3, -4, -5}, {1, 3, 1, 3, 1}, {0, 1, 0, 1, 0}, {-1, -1, -1, -1, -1}}; double n[MAT_SIZE] [MAT_SIZE] = {{2, 1, 5, 0, 2}, {1, 4, 3, 2, 7}, {4, 4, 4, 4, 4}, {7, 1, -1, -1, -1}, {0, 0, 8, -1, -6}}; // fixed size dynamic matrix DynMat mDyn, nDyn, ansDyn; // allocate and load for (int r = 0; r > mat_size, smallPercent; // non fixed size dynamic matrix for Sparse Matrix float *matDynSp[mat_size], *matDynSpAns[mat_size]; // allocate rows and initialize to o for (r = 0; I