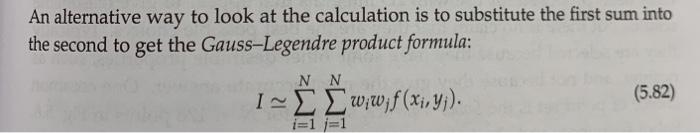ONLY NEED THE CODE FOR PART (B) in Python code v3.9 PLEASE!!

Eq(5.82):
Exercise 5.14: Gravitational pull of a uniform sheet square A uniform sheet of metal is floating motionless in space 1kg point mass 10m The sheet is 10m on a side and of negligible thickness, and it has a mass of 10 metric tonnes. a) Consider the gravitational force due to the plate felt by a point mass of 1kg a distance z from the center of the square, in the direction perpendicular to the sheet, as shown above. Show that the component of the force along the z-axis is F = Goz - SL12 (42 +42 +42352 where G = 6.674 x 10-11 m kg 's-2 is Newton's gravitational constant and o is the mass per unit area of the sheet. b) Write a program to calculate and plot the force as a function of 2 from 2 = 0 10 m. For the double integral use (double) Gaussian quadrature, as in Eq. (5.82), with 100 sample points along each axis. c) You should see a smooth curve, except at very small values of z, where the force should drop off suddenly to zero. This drop is not a real effect, but an artifact of the way we have done the calculation. Explain briefly where this artifact comes from and suggest a strategy to remove it, or at least to decrease its size. This calculation can thought of as a model for the gravitational pull of a galaxy. Most of the mass in a spiral galaxy (such as our own Milky Way) lies in a thin plane or disk passing through the galactic center, and the gravitational pull exerted by that plane on bodies outside the galaxy can be calculated by just the methods we have employed to z here. An alternative way to look at the calculation is to substitute the first sum into the second to get the Gauss-Legendre product formula: I- Lw;w;f (x,y;). (5.82) i=1=1 Exercise 5.14: Gravitational pull of a uniform sheet square A uniform sheet of metal is floating motionless in space 1kg point mass 10m The sheet is 10m on a side and of negligible thickness, and it has a mass of 10 metric tonnes. a) Consider the gravitational force due to the plate felt by a point mass of 1kg a distance z from the center of the square, in the direction perpendicular to the sheet, as shown above. Show that the component of the force along the z-axis is F = Goz - SL12 (42 +42 +42352 where G = 6.674 x 10-11 m kg 's-2 is Newton's gravitational constant and o is the mass per unit area of the sheet. b) Write a program to calculate and plot the force as a function of 2 from 2 = 0 10 m. For the double integral use (double) Gaussian quadrature, as in Eq. (5.82), with 100 sample points along each axis. c) You should see a smooth curve, except at very small values of z, where the force should drop off suddenly to zero. This drop is not a real effect, but an artifact of the way we have done the calculation. Explain briefly where this artifact comes from and suggest a strategy to remove it, or at least to decrease its size. This calculation can thought of as a model for the gravitational pull of a galaxy. Most of the mass in a spiral galaxy (such as our own Milky Way) lies in a thin plane or disk passing through the galactic center, and the gravitational pull exerted by that plane on bodies outside the galaxy can be calculated by just the methods we have employed to z here. An alternative way to look at the calculation is to substitute the first sum into the second to get the Gauss-Legendre product formula: I- Lw;w;f (x,y;). (5.82) i=1=1