Options for the first and second blank are either higher or lower and the options for the third blank is to choose to either invite or not to invite
Please help with graph placement as well thank you !
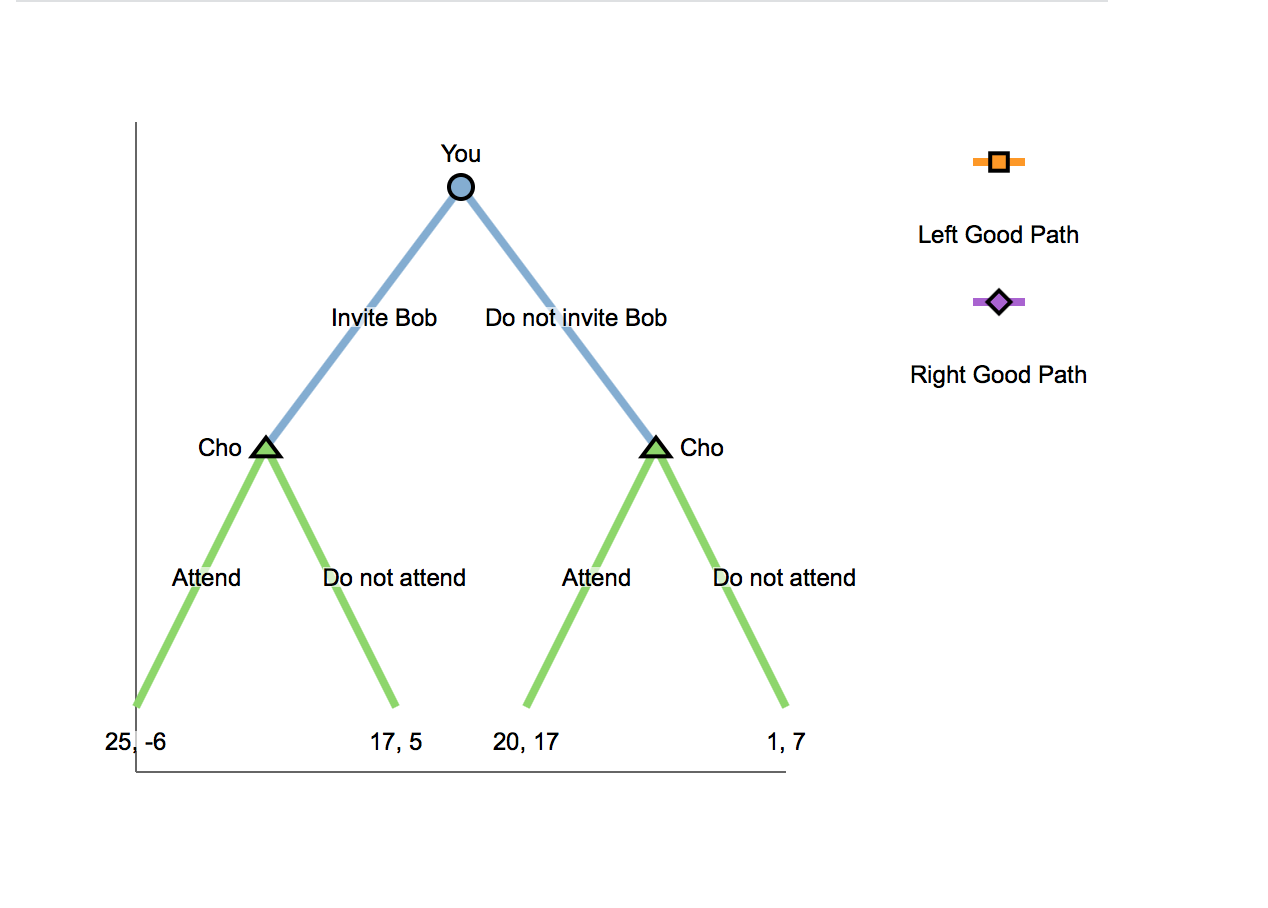
6. Backward induction and subgame-perfect Nash equilibria Backward induction is a useful tool while solving for the subgame-perfect Nash equilibrium (SPNE) of a sequential game. This problem walks you through how to nd the SPNE in the following game using this method. Suppose you are creating the invite list for an upcoming party, but you face a dilemma about two of your friends. Everyone knows that your friend Bob never misses a party if invited. However, if you invite Bob, you are concerned that your friend Cho may not attend because of their recent breakup. Since you are doing your invitation online, Cho can observe whether you choose to invite Bob. The following game tree represents the game you face. At each node, your payoff is shown first, Cho's second: You O O Left Good Path Invite Bob Do not invite Bob Right Good Path Cho A A Cho Attend Do not attend Attend Do not attend 25,-6 17, 5 20, 17 1, 7To nd the SPNE using backward induction, you must rst start at the end of the game, or at Cho's decision. Since you act rst and Cho can observe this action, she can make a different decision depending on which node she faces. Suppose that you decide to invite Bob to the party. If Cho attends, she will receive a V payoff than if she does not attend. Now that you have determined which action yields the higher payoff, mark the leg off the left node corresponding to the action that represents the good path on the diagram with an orange line (square symbol). (Note: You will not be graded on your manipulation of the diagram.) Now suppose that you decide not to invite Bob. If Cho attends, she will receive a V payoff than if she does not attend, given that you do not invite Bob. Again, mark the leg off the right node corresponding to the action that represents the good path on the diagram with a purple line (diamond symbol). (Note: You will not be graded on your manipulation of the diagram.) It is now time for your decision. You have already determined what Cho will do, given your decision to invite or not invite Bob. Since you can internalize this future decision of Cho's, you need only to examine your payoffs for the two good paths. Comparing these two payoffs, you will choose v Bob to your party. What is the subgame-perfect Nash equilibrium of this game? A You do invite Bob, and Cho attends if Bob is not invited and does not attend if Bob is invited. A You do not invite Bob, and Cho attends if Bob is not invited and does not attend if Bob is invited. A You do not invite Bob, and Cho attends. A You do not invite Bob, and Cho attends if Bob is invited and does not attend if Bob is not invited