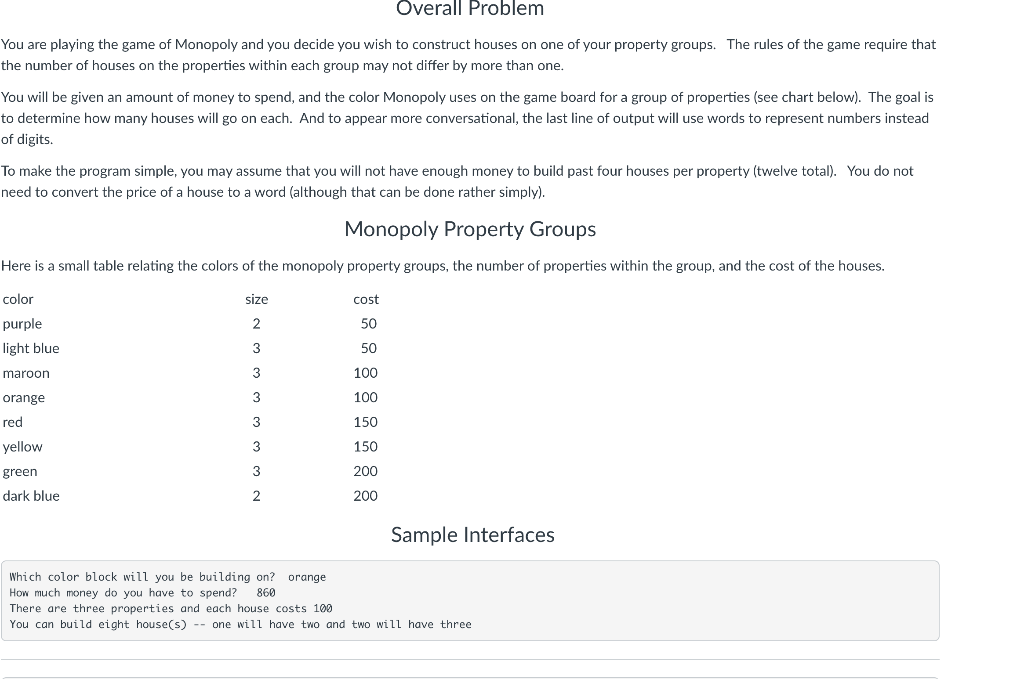
Overall Problem You are playing the game of Monopoly and you decide you wish to construct houses on one of your property groups. The rules of the game require that the number of houses on the properties within each group may not differ by more than one. You will be given an amount of money to spend, and the color Monopoly uses on the game board for a group of properties (see chart below). The goal is to determine how many houses will go on each. And to appear more conversational, the last line of output will use words to represent numbers instead of digits. To make the program simple, you may assume that you will not have enough money to build past four houses per property (twelve total). You do not need to convert the price of a house to a word (although that can be done rather simply). Monopoly Property Groups Here is a small table relating the colors of the monopoly property groups, the number of properties within the group, and the cost of the houses. color size cost 2 50 purple light blue 3 50 maroon 3 100 orange 3 100 red 3 150 3 150 yellow green dark blue 3 200 2 200 Sample Interfaces Which color block will you be building on? orange How much money do you have to spend? 860 There are three properties and each house costs 100 You can build eight house(s) -- one will have two and two will have three buses Outer prope may have level tilall our). The inputs to the program will be essentially the same -- the color of a property group and the amount of money to be spent. But the following cases should be addressed: if no building is affordable, display "You cannot afford even one house." instead of building 0 houses everywhere. If any property could have 5 houses, announce that such properties would have a hotel instead. if any property could have more than 5 houses, still only build one hotel there, and nothing more omit the word 'none' in the output (i..e don't say 'one property has none' or 'none have two") Comparing Homework 2 to Homework 3 The difference in these programs primarily appears in the final output statement: Hypothetical Homework 2 Output Corresponding Homework 3 Output three will have none and none will have one You cannot afford even one house. one will have one and two will have two one will have one and two will have two one will have none and two will have one two will have one three will have one three will have three three will have one and none will have two three will have three and none will have four two will have four and one will have five two will have five and none will have six one will have seven and two will have eight two will have four and one will have a hotel two will have a hotel three will have a hotel Hint: The simplest and clearest solutions will use 'else' and 'elif' and will not need 'and' or 'or'. A portion of your grade is based on how clear your code is, and how well it avoids producing contradictory output. Note: All of these decisions in this chart are entirely based on the results of the previous program, so your code should do the same -- wait until the calculations are complete before deciding how to display the results. Do not make your program unnecessarily complicated by trying to identify the different cases before doing any math. Also Note: three hotels have the cost of 15 houses, which will require a slight modification to the collection of words used to display numbers in the previous assignment. If the number of houses one can afford exceeds 15 (that last row above could have afforded 23), just display the numeric value itself, without converting to a word. Overall Problem You are playing the game of Monopoly and you decide you wish to construct houses on one of your property groups. The rules of the game require that the number of houses on the properties within each group may not differ by more than one. You will be given an amount of money to spend, and the color Monopoly uses on the game board for a group of properties (see chart below). The goal is to determine how many houses will go on each. And to appear more conversational, the last line of output will use words to represent numbers instead of digits. To make the program simple, you may assume that you will not have enough money to build past four houses per property (twelve total). You do not need to convert the price of a house to a word (although that can be done rather simply). Monopoly Property Groups Here is a small table relating the colors of the monopoly property groups, the number of properties within the group, and the cost of the houses. color size cost 2 50 purple light blue 3 50 maroon 3 100 orange 3 100 red 3 150 3 150 yellow green dark blue 3 200 2 200 Sample Interfaces Which color block will you be building on? orange How much money do you have to spend? 860 There are three properties and each house costs 100 You can build eight house(s) -- one will have two and two will have three buses Outer prope may have level tilall our). The inputs to the program will be essentially the same -- the color of a property group and the amount of money to be spent. But the following cases should be addressed: if no building is affordable, display "You cannot afford even one house." instead of building 0 houses everywhere. If any property could have 5 houses, announce that such properties would have a hotel instead. if any property could have more than 5 houses, still only build one hotel there, and nothing more omit the word 'none' in the output (i..e don't say 'one property has none' or 'none have two") Comparing Homework 2 to Homework 3 The difference in these programs primarily appears in the final output statement: Hypothetical Homework 2 Output Corresponding Homework 3 Output three will have none and none will have one You cannot afford even one house. one will have one and two will have two one will have one and two will have two one will have none and two will have one two will have one three will have one three will have three three will have one and none will have two three will have three and none will have four two will have four and one will have five two will have five and none will have six one will have seven and two will have eight two will have four and one will have a hotel two will have a hotel three will have a hotel Hint: The simplest and clearest solutions will use 'else' and 'elif' and will not need 'and' or 'or'. A portion of your grade is based on how clear your code is, and how well it avoids producing contradictory output. Note: All of these decisions in this chart are entirely based on the results of the previous program, so your code should do the same -- wait until the calculations are complete before deciding how to display the results. Do not make your program unnecessarily complicated by trying to identify the different cases before doing any math. Also Note: three hotels have the cost of 15 houses, which will require a slight modification to the collection of words used to display numbers in the previous assignment. If the number of houses one can afford exceeds 15 (that last row above could have afforded 23), just display the numeric value itself, without converting to a word