Overview

The Traveling Salesman Problem (TSP) is a classic optimization problem that has practical applications in various fields, including logistics, transportation, and manufacturing. In the TSP, a salesperson is tasked with finding the shortest possible route that visits a set of cities and returns to the starting city. The objective is to minimize the total distance traveled while ensuring that each city is visited exactly once. This problem is known to be NP-hard, meaning that finding the optimal solution becomes computationally infeasible as the number of cities increases.

Various techniques and algorithms have been developed to tackle the TSP, and one of the effective approaches is the use of Genetic Algorithms (GA). Genetic Algorithms are heuristic optimization methods inspired by the principles of natural selection and evolution. They provide a powerful means to search for near-optimal solutions in complex and combinatorial optimization problems like the TSP.

This project is dedicated to solving the Traveling Salesman Problem using a Genetic Algorithm implemented in C++. The primary goal is to employ the GA to find a near-optimal tour for the salesperson that minimizes the total distance traveled. The project will include the development of a C++ program that reads input data representing the city graph, applies the Genetic Algorithm to find an approximate solution, and outputs the best tour found along with its total distance.

By implementing and experimenting with a Genetic Algorithm, this project aims to showcase an effective heuristic approach to solving NP-hard optimization problems and provide a practical solution for finding efficient routes in real-world scenarios.

Project Description

Traveling Salesman Problem (TSP)

The Traveling Salesman Problem (TSP) is a fundamental combinatorial optimization problem characterized by the following key aspects:

Shortest Possible Tour: The primary objective of the TSP is to find the shortest possible tour that enables a salesperson to visit a predefined set of cities exactly once and return to the starting city. In this context, a "tour" refers to the sequence in which the cities are visited, forming a closed loop.

Cities as Nodes: In the TSP, the cities are typically represented as nodes or vertices in a graph. Each city is connected to every other city through edges or arcs, and these connections define the distances or edge weights between cities. These distances represent the cost or distance associated with traveling from one city to another.

Permutation of Cities: The fundamental goal of the TSP is to determine a permutation of cities that results in the minimum total distance traveled. This permutation represents the optimal order in which the cities should be visited to minimize the salesperson's travel distance. It is worth noting that the starting and ending point of the tour is usually the same city, as the salesperson returns to the initial location after visiting all cities.

Genetic Algorithm (GA)

• The Genetic Algorithm is a heuristic optimization technique inspired by the process of natural selection.
• GA uses the principles of selection, crossover (recombination), mutation, and population evolution to search for optimal solutions.
• In this project, the GA is used to evolve and improve solutions to the TSP.

General Steps of Genetic Algorithm

The Genetic Algorithm (GA) employed to solve the Traveling Salesman Problem (TSP) follows a series of well-defined steps to iteratively evolve and improve candidate solutions:

Initialization: At the beginning of the GA process, an initial population of candidate solutions, also known as tours, is created. In the context of the TSP, this involves generating a set of random permutations of cities. Each permutation represents a different tour.

Selection: The selection step involves choosing parent solutions from the current population based on their fitness, which in the case of the TSP, corresponds to the shortness of the tour. The project employs the tournament selection method, where individuals are randomly grouped into tournaments, and the fittest individuals from each tournament are selected as parents for the next generation.

Crossover (Recombination): In the crossover step, offspring solutions are created by combining genetic material from two parent solutions. For this project, ordered crossover (also known as partially mapped crossover) is used. It involves selecting a segment of one parent's tour and filling in the remaining cities with the order from the other parent's tour. The crossover rate parameter is used to control the likelihood of crossover occurring.

Mutation: Mutation introduces small random changes into some offspring solutions. In this project, swap mutation is applied, which means that with a certain mutation rate, two cities in the tour are randomly selected and swapped. This introduces diversity and helps avoid getting stuck in local optima.

Replacement: In the replacement step, old solutions in the current population are replaced with the new offspring solutions. The goal is to maintain the population size and replace less fit solutions with potentially better ones.

Termination: The iterative process of selection, crossover, mutation, and replacement is repeated for a fixed number of generations or until a termination criterion is met. The termination criterion could be a maximum number of generations, convergence of the best tour found, or a time limit. In this project, we will use the number of generations for simplicity.

Genetic Algorithm Parameters

There are four major parameters that should be included. You can pass them as parameters to the constructor of the algorithm. You will need to tweak their values if your algorithm does not run efficiently. I will suggest some good starting values here.

• Population size You can start with 10 times of the number of cities.
• Number of generations You can start with 100 times of the number of cities.
• Crossover rate Start with 0.8
• Mutation rate Start with 0.2

The algorithm class

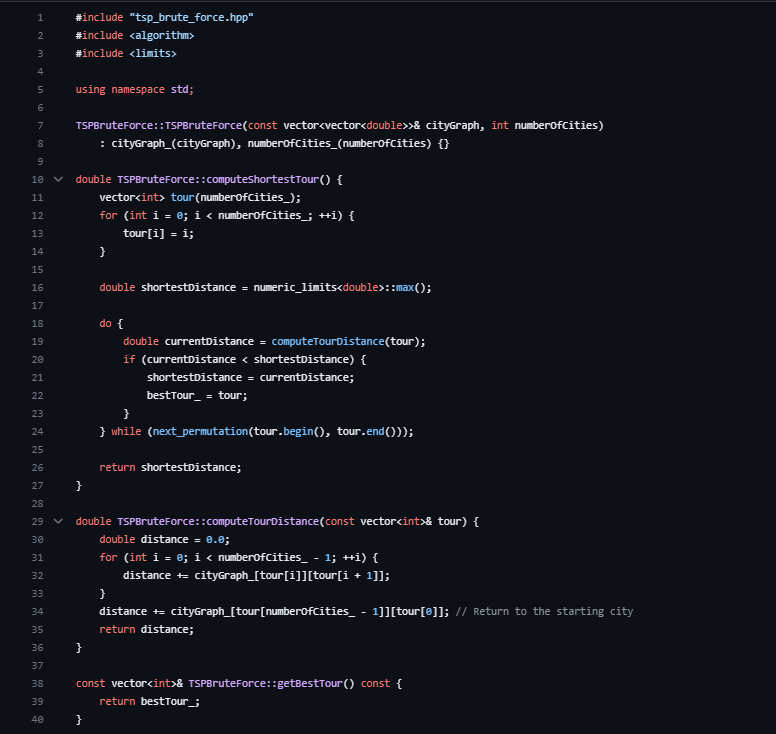
Refer to the provided brute-force algorithm for the recommended interface for the algorithm.

• .computeShortestTour() to return the distance of the best tour
• .getBestTour() to return the tour as a vector type value

Input CSV File

To facilitate the Traveling Salesman Problem (TSP) solving process, it's essential to efficiently handle the input CSV file containing connectivity information. The following steps outline how to process the data:

Input File Format: The provided input CSV file has the following format:

• The file contains 20 lines of 20 comma-separated double values.
• The values represent distances or costs between cities in a symmetric manner over the diagonal line. It means that the city graph is an undirected graph.
• Assuming that all cities are connected, there are no missing values in the matrix.

Data Representation: Store the connectivity data from the CSV file in a data structure that allows efficient access. For this project, it is recommended to use a vector of vector of double data structure. Each inner vector represents a row of the matrix, and the outer vector holds all the rows, forming a 2D matrix-like structure.

main executable

• Your main executable should be similar to the provided driver for the brute-force algorithm in terms of command-line arguments and output format.
• Number of Cities Parameter: Implement a parameter that allows users to specify the number of cities (n, up to 20) to include in the TSP problem-solving process. This parameter enables flexibility in experimenting with different city counts. The algorithm should only consider the first n cities from the input file when solving the TSP.
• Your run should take the same parameter as the provided brute-force driver like ./main cities.csv 5. It should print the output in the same format too.
• You may not get the best result every time in your run! It is because GA does not guarantee that. However, your result should at least get close to the best and can provide the best result frequently.
• Remember that a tour can be displayed in various ways! E.g. The tour 0 1 2 3 4 0 is the same as 3 4 0 1 2 3.

Baseline Brute Force Algorithm

A baseline brute force algorithm and its driver have been provided as a reference and for comparison purposes. The brute force algorithm exhaustively explores all possible permutations of cities to find the optimal tour. While it is not suitable for large instances of the TSP, it serves as a benchmark for evaluating the effectiveness of the Genetic Algorithm (GA) solution.

In the provided codebase, the brute force algorithm is encapsulated in a class and can be used for TSP problem-solving.

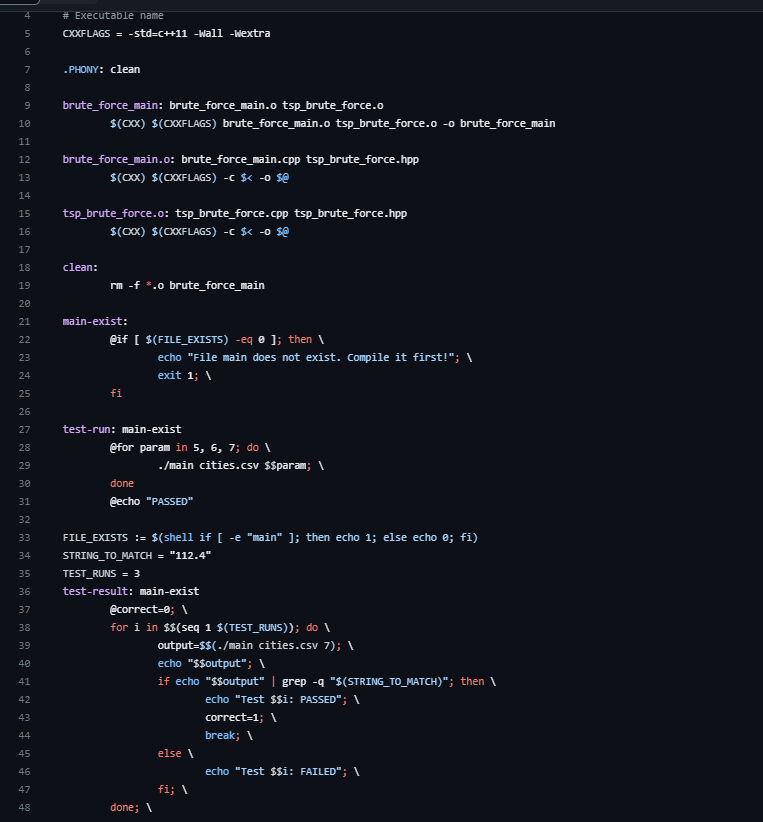
You can compile it using the command make -f test.mk brute_force_main and run it using ./brute_force_main cities.csv .<>

You can always find the best result using the brute force algorithm.

This baseline also serve as a guide on how to write agenetic algorithm driver and corresponding makefile. It will also show you the best solution to the TSP with the given data.

Please be aware that this algorithm may be super slow when the is big In my experiment, when n is greater than 12, it will take very long time.

Report

Please make a report based on the results you get and compare them with that for the brute force algorithm. Put your results of runs with various number of cities and record them in tables. Make a plot over the problem size (number of cities) for each algorithm and compare the two algorithm in one paragraph. You can limit the problem sizes to the range from 6 to 10.

Requirements

• Implement a Genetic Algorithm to solve the TSP.
• Make a driver main.cpp to run the algorithm and measure the time.
• Display the best tour found and its distance to the screen.
• a makefile to compile the executable named main.
• Document the essential entities (class, method) in the header file using documentation comments.

brute_force_main.cpp

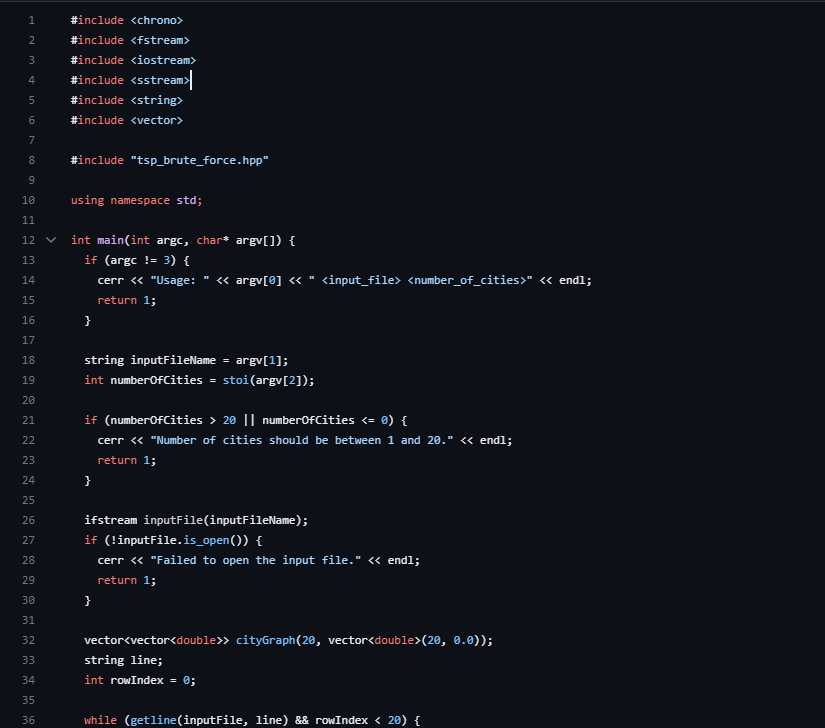
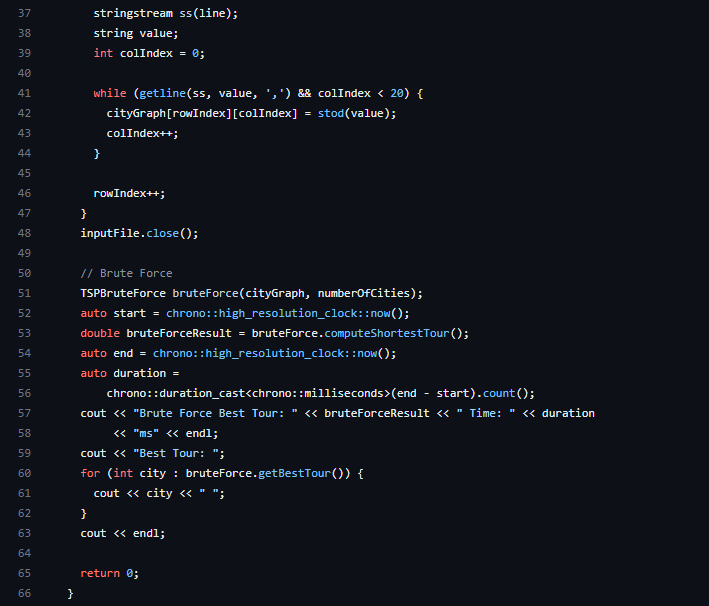
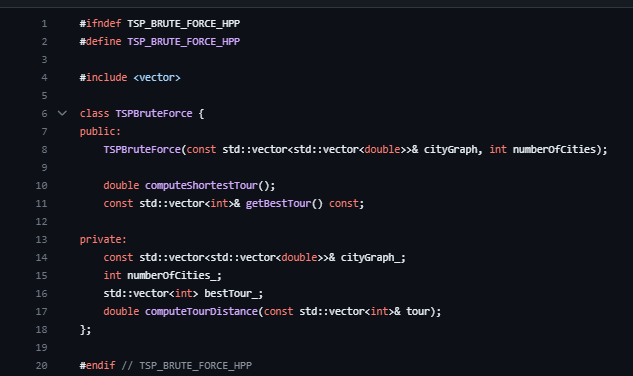
#include #include #include #include 5 #include 6 #include #include "tsp_brute_force.hpp" 9 10 using namespace std; 11 12 int main(int argc, char* argv) { 13 if (argc != 3) { 14 cerr " 20 | | numberOfCities > cityGraph(20, vector(20, 0.0)); 33 string line; 34 int rowIndex = 0; 35 36 while (getline(inputFile, line) && row Index (end - start) . count(); 57 cout #include using namespace std; 6 7 TSPBruteForce: : TSPBruteForce(const vector>& cityGraph, int numberofCities) : cityGraph_(cityGraph), numberofCities_(numberofcities) {} 9 10 double TSPBruteForce: : computeshortestTour() { 11 vector tour(numberofCities_); 12 for (int i = 0; i : :max(); 17 18 do { 19 double currentDistance = computeTourDistance(tour); 20 if (currentDistance & tour) { 30 double distance = 0.0; 31 for (int i = 0; i & TSPBruteForce: : getBestTour() const { 39 return bestTour_; 40 }\f