Overview:

This project asks you to evaluate the four sorting algorithms we have dis- cussed in class on various inputs and relate their theoretical run time to their empirical (actual) behavior. These algorithms are SelectionSort, Insertion- Sort, MergeSort, and QuickSort. In the interests of time, you have been provided with code that implements all four algorithms and can run them on inputs of varying sizes and types.

Running the provided program:

Along with this document, you have been provided with source code and a Makefile for the various sorting algorithms and input types to test in this project. This program will run the specified algorithm (SelectionSort, Inser- tionSort, MergeSort, or QuickSort) on a sorted, random, or constant input array of a given size. I expect that you can use an IDE or the Linux make utility in order to compile the code. Once compiled, the program should be run from the command line, as it expects three arguments. If fewer than three arguments are specified, the program will assume default variables for any unspecified arguments.

The first of these three arguments represents the size of the input ar- ray. The program only accepts sizes between 1 and 1,000,000,000, inclusive (default 10,000). The second argument represents the sorting algorithm you wish to run. Valid algorithms include SelectionSort, InsertionSort, Merge- Sort, and QuickSort (default MergeSort), or you can abbreviate the algo- rithms by their first letter (s, i, m,, or q). The last argument represents

the type of input to sort. Valid input types are sorted, random, and constant (or s, r, c; default r), where random is an unsorted array, sorted is a sorted array (in increasing order), and constant is an array where every entry is identical.

In order to improve the timing stability, the algorithm runs the requested sort three times and reports the median of the three timing results to you. In order to get the most accurate timing results, there should be no other processes running on the machine at the same time, but this may not always be possible, especially if you are running the program on a lab machine.

Results:

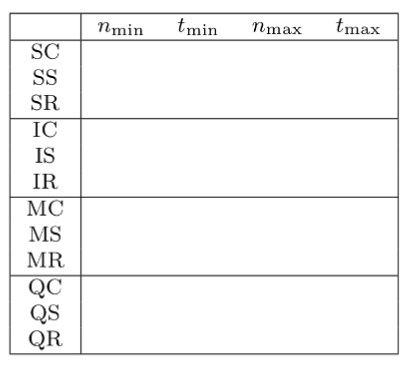
Run each of the four sorting algorithms on constant, sorted, and random arrays that are powers of 10. For each of the twelve cases, you should record the following:

1. nmin: the smallest power of 10 array size that takes 20 milliseconds or more per run to sort;

2. tmin: the time to sort an array of size nmin;

3. nmax: the largest power of 10 array size that takes 10 minutes or less per run to sort (30 mins for all 3 runs), or the largest input size you can successfully sort if no input took more than 30 minutes total;

4. tmax: the time required to sort nmax elements.

Note, you may need to ensure that you have sufficient stack space before testing QuickSort to ensure that you do not run out (stack overflow). You can run ulimit -s unlimited in Linux before executing the algorithm to increase the available stack space. This parameter can also be changed in many IDEs on Mac and Windows; consult the appropriate documentation if this becomes a problem.

If you are having trouble running the program on an array of 1 billion elements (or running large arrays with QuickSort), I recommend using a somewhat smaller array, like 500 or 250 million. The goal of this project is to find a nmin and nmax that are sufficiently far apart that the growth rate of the time complexity can be approximated using the timing and input size ratios. The descriptions of nmin and nmax given above are just to give you a reasonable idea of how to find good array sizes; finding the exact value of nmin that takes 20 milliseconds to run, for instance, is not critical.

If you are having trouble getting good timing results (e.g., one power- of-ten gives good timing results, but the next is too long and the previous too quick), you may try using intermediate input sizes, such as 3.2 10x, 1.8 10x, or 5.6 10x. You may also use different systems to perform the tests for different algorithm/input combinations, but obviously, youll want all of the runs for a single experiment to be on the same machine, as computing a timing ratio with results from different machines is virtually meaningless.

You should enter your results into a comma-separated value (CSV) file. The CSV file should contain 5 columns and 13 rows. Your first column should label the 12 different experiments, while the first row labels the experiment variables (nmin, tmin, nmax, and tmax). Your row labels should include the algorithm name (SelectionSort, InsertionSort, MergeSort, or Quicksort) and input type (Sorted, Random, or Constant). You may abbreviate these labels as S, I, M, Q, and S, R, C. (For example, SS represents your SelectionSort result on a sorted array.) An example table appears below. You may use Excel (or any other software) to prepare your data.

(Picture 1 below)

Analysis:In this section, you will estimate the complexity of the four algorithms by comparing the ratio between tmin and tmax to ratios representing the com- plexity of the algorithm. Specifically, you should compute f(nmax)/f(nmin) for f1(n) = n, f2(n) = nln(n), and f3(n) = n2. You should round to the nearest integer when computing these ratios. Finally, you should label each experiment according to the ratio tmax/tmin most resembles.

For example, if one of your experiments resulting in nmin = 100 and

nmax =10,000,000,yourratioswouldbef1(nmax)/f1(nmin)10,000,000/100=

100, 000, f2(nmax)/f2(nmin) = 10, 000, 000 ln(10, 000, 000)/(100 ln(100)) = 350, 000, and f3(nmax)/f3(nmin) = 10,000,0002/1002 = 10,000,000,000. You would

then label the algorithm based on which of these three ratios tmax/tmin is closest to.

As part of your report, you should create a chart that includes the com- puted ratios as well as the behavior of the algorithm (Linear, nlgn, or Quadratic), across all 12 experiments. An example chart appears below: ( picture 2 below)

tmax/tmin n ratio n ln(n) ratio n2 ratio Behavior

SC SS SR

IC IS IR

MC MS MR

QC QS QR

You should then write a summary of (1) how your results compare to the theoretical analysis for the three algorithms (below), and (2) why your results make sense or are surprising. You should spend more time explaining your results when they are unusual or unexpected.

#ifndef __SORTING_HPP

#define __SORTING_HPP

#include

#include "Helper.hpp"

/**

Template implementation of SelectionSort

Note: the input type must define the

for the code to compile

@param data input array

@param n the length of the input array

*/

template T* selectionsort(T* data, int n)

{

for (int i = 0; i

{

int minloc = i;

for (int j = i+1; j

if (data[j]

minloc = j;

Swap(data[i], data[minloc]);

}

return data;

}

/**

Template implementation of InsertionSort (iterative)

Note: the input type must define the

for the code to compile

@param data input array

@param n the length of the input array

*/

template T* insertionsort(T* data, int n)

{

for (int i = 1; i

{

int ins = data[i];

int shift = i;

while (shift > 0 && ins

{

data[shift] = data[shift-1];

shift = shift - 1;

}

data[shift] = ins;

}

return data;

}

/**

Template implementation of MergeSort (recursive)

Note: the input type must define the

for the code to compile

Also, the third argument must be an allocated array with at least n elements

@param data input array

@param n the length of the input and temp arrays

@param temp a temporary array used to merge the sub-arrays together

*/

template T* mergesort(T* data, int n, T* temp)

{

if (n > 1)

{

int mid = (n+1) / 2;

T* left = mergesort(data, mid, temp);

T* right = mergesort(data+mid, n-mid, temp);

int l = 0;

int r = 0;

int s = 0;

while (l

{

if (left[l]

temp[s++] = left[l++];

else

temp[s++] = right[r++];

}

while (l

temp[s++] = left[l++];

while (r

temp[s++] = right[r++];

memcpy(data, temp, s*sizeof(T));

}

return data;

}

/**

Template implementation of SelectionSort

Note: the input type must define the

for the code to compile

@param data input array

@param n the length of the input array

*/

template T* quicksort(T* data, int n)

{

if (n

return data;

int mid = (n+1) / 2;

int pivot = mid;

if (data[0]

{

if (data[mid]

pivot = 0;

else if (data[n-1]

pivot = n-1;

}

else if (data[mid]

pivot = n-1;

else if (data[0]

pivot = 0;

Swap(data[0], data[pivot]);

int left = 1;

int right = n-1;

do

{

while (left

left++;

while (left

right--;

Swap(data[left], data[right]);

} while (left

if (data[0]

left--;

Swap(data[0], data[left]);

quicksort(data, left);

quicksort(data+left+1, n-left-1);

return data;

}

#endif

Picture 1

Picture 2

nmint tmin nmaxtmax SC SR IC IS IR MC MS MR Qc QS QR