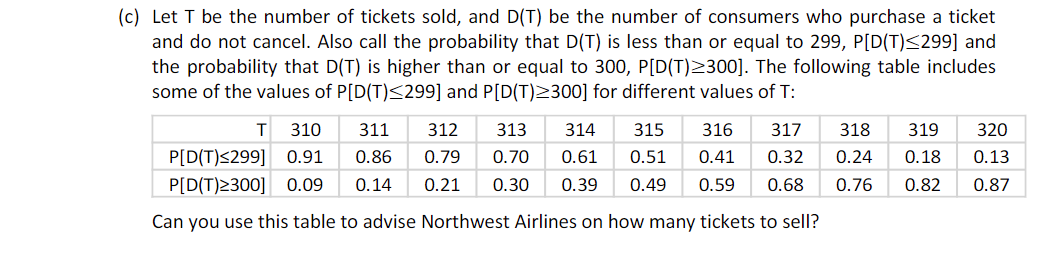
P3. Airline Northwest Airlines runs daily flights from Austin to Chicago. They face a fixed cost of $70,000 for each flight regardless of the actual number of passengers on the plane. There are 300 seats available on each plane. One-way tickets generate revenue $600 apiece if used, but cancelations are fully refundable. All posted tickets are sold (there is always enough demand), however each customer who purchases a ticket has a 5% probability of cancelling. By law, an airline is allowed to overbook flights (sell more tickets than available seats) but must give a compensation of $250 to all ticketed passengers who are not allowed to board. In addition, it must provide those passengers with alternative transportation on another carrier (the cost of alternative transportation just cancels out the $600 revenue). The goal of the problem is to figure out how many tickets Northwest Airlines should post on a typical flight from Austin to Chicago. (a) Based on the parameters of the problem, do you think the airline should overbook or not? Try to support your position with quantitative arguments. (b) What are the marginal gains (MG) and marginal losses (ML) form increasing the number of tickets posted (and thus sold) by one? [Hint: Call the number of tickets posted/sold T, and the number of customers who purchase a ticket and do not cancel D(T)---where D stands for demand. Then, you can express MG and ML in terms of the probability that D(T) is less than or equal to 299, P[D(T)299] and the probability that D(T) is higher than or equal to 300, P[D(T)300]] (c) Let T be the number of tickets sold, and D(T) be the number of consumers who purchase a ticket and do not cancel. Also call the probability that D(T) is less than or equal to 299, P[D(T)299] and the probability that D(T) is higher than or equal to 300, P[D(T)300]. The following table includes some of the values of P[D(T)299] and P[D(T)300] for different values of T: (c) Let T be the number of tickets sold, and D(T) be the number of consumers who purchase a ticket and do not cancel. Also call the probability that D(T) is less than or equal to 299, P[D(T) 299] and the probability that D(T) is higher than or equal to 300, P[D(T)300]. The following table includes some of the values of P[D(T)299] and P[D(T)300] for different values of T: T 310 311 312 313 314 P[D(T)299] P[D(T)300] 0.09 0.14 0.91 0.86 0.79 0.70 0.61 0.21 0.30 0.39 315 0.51 0.49 316 317 318 0.59 0.41 0.32 0.68 319 320 0.24 0.18 0.13 0.76 0.82 0.87 Can you use this table to advise Northwest Airlines on how many tickets to sell?