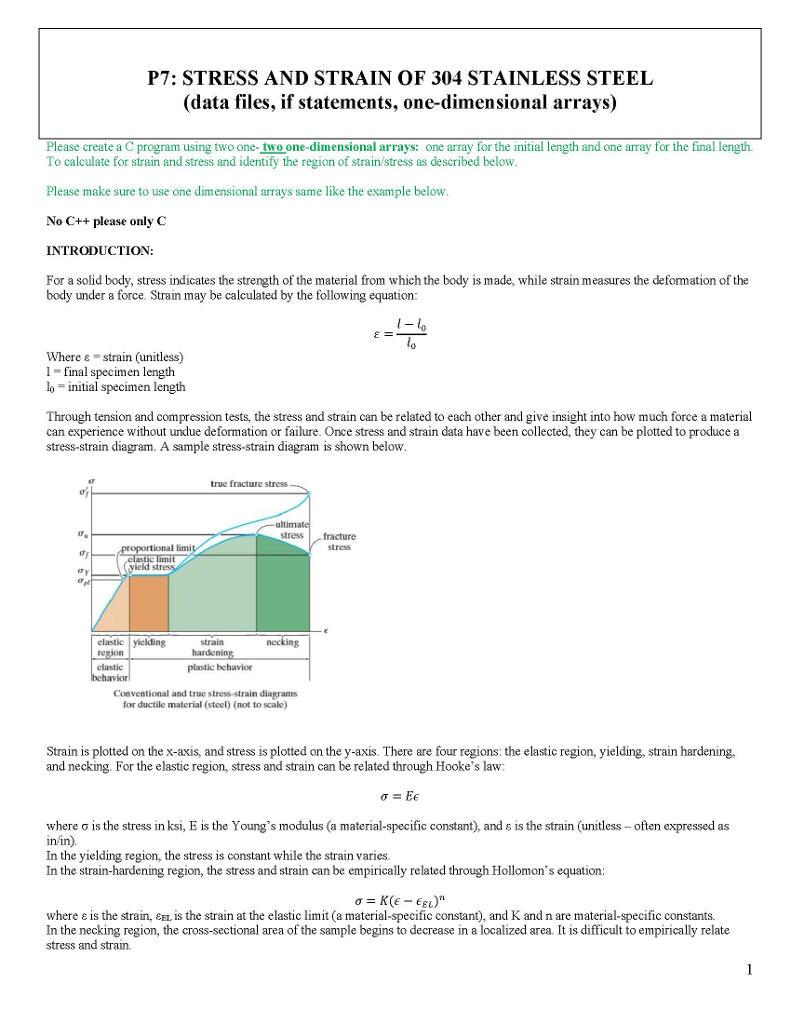



P7: STRESS AND STRAIN OF 304 STAINLESS STEEL (data files, if statements, one-dimensional arrays) Please create a C program using two one-two one-dimensional arrays: one array for the initial length and one array for the final length To calculate for strain and stress and identify the region of strain/stress as described below Please make sure to use one dimensional arrays same like the example below No C++ please only C INTRODUCTION: For a solid body, stress indicates the strength of the material from which the body is made, while strain measures the deformation of the body under a force. Strain may be calculated by the following equation lo where = strain (unitless) 1-final specimen length lo initial specimen length Through tension and compression tests, the stress and strain can be related to each other and give insight into how much force a material can experience without undue deformation or failure. Once stress and strain data have been collected, they can be plotted to produce a stress-strain diagram. A sample stress-stra in diagram is shown below true fracture stress 0 stress fracture stress l limi vield elastic |yielding strain necking clastic plastic behavior Conventional and true stress-strain diagrams for ductile material (steel) (not to scale) Strain is plotted on the x-axis, and stress is plotted on the y-axis. There are four regions: the elastic region, yielding, strain hardening. and necking. For the elastic region, stress and strain can be related through Hooke's law: where is the stress in ksi, E is the Young's rmoduus (a material-specific constant), and g Is the strain (unitless-often expressed as in/in). In the yielding region, the stress is constant while the strain varies. In the strain-hardening region, the stress and strain can be empirically related through Hollomon's equation = K(E-EEL)" where is the strain, Elis the strain at the elastic limit (a material-specific constant, and K and n are material-specific constants. In the necking region, the cross-sectional area of the sample begins to decrease in a localized area. It is difficult to empirically relate stress and strain. P7: STRESS AND STRAIN OF 304 STAINLESS STEEL (data files, if statements, one-dimensional arrays) Please create a C program using two one-two one-dimensional arrays: one array for the initial length and one array for the final length To calculate for strain and stress and identify the region of strain/stress as described below Please make sure to use one dimensional arrays same like the example below No C++ please only C INTRODUCTION: For a solid body, stress indicates the strength of the material from which the body is made, while strain measures the deformation of the body under a force. Strain may be calculated by the following equation lo where = strain (unitless) 1-final specimen length lo initial specimen length Through tension and compression tests, the stress and strain can be related to each other and give insight into how much force a material can experience without undue deformation or failure. Once stress and strain data have been collected, they can be plotted to produce a stress-strain diagram. A sample stress-stra in diagram is shown below true fracture stress 0 stress fracture stress l limi vield elastic |yielding strain necking clastic plastic behavior Conventional and true stress-strain diagrams for ductile material (steel) (not to scale) Strain is plotted on the x-axis, and stress is plotted on the y-axis. There are four regions: the elastic region, yielding, strain hardening. and necking. For the elastic region, stress and strain can be related through Hooke's law: where is the stress in ksi, E is the Young's rmoduus (a material-specific constant), and g Is the strain (unitless-often expressed as in/in). In the yielding region, the stress is constant while the strain varies. In the strain-hardening region, the stress and strain can be empirically related through Hollomon's equation = K(E-EEL)" where is the strain, Elis the strain at the elastic limit (a material-specific constant, and K and n are material-specific constants. In the necking region, the cross-sectional area of the sample begins to decrease in a localized area. It is difficult to empirically relate stress and strain










