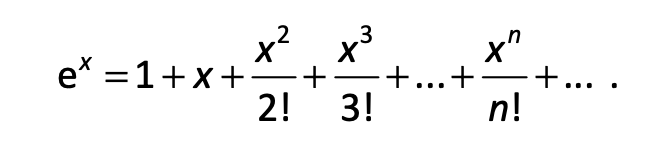
Part 1: Complete the statements below in a MATLAB function file named IterMeth.m to have it compute the Maclaurin series expansion of the exponential function. Details are given within the text boxes.

function [fx,ea,iter] = IterMeth(x,es,maxit) % Maclaurin series of exponential function % [fx,ea,iter] = IterMeth(x,es,maxit) % Input: % x = value at which the series is evaluated % es = stopping criterion (default = 0.0001) % maxit = maximum iterations (default = 50) % Output: % fx = estimated value % ea = approximate relative error (%) % iter = number of iterations % Defaults: if (nargin=maxit), break, end end fx = sol; end

Part 2: Make a MATLAB script file to call the function IterMeth with the input parameters shown here.

clc; clear all; close all; format long sol_ref = exp(1) [sol1,ea1,iter1] = IterMeth(1,1e-1,50) [sol2,ea2,iter2] = IterMeth(1,1e-2,50) [sol3,ea3,iter3] = IterMeth(1,1e-3,50) [sol4,ea4,iter4] = IterMeth(1,1e-4,50) [sol5,ea5,iter5] = IterMeth(1,1e-5,50) 

When you run this MATLAB script file, with its calls to the IterMeth function, what do you see? Can you explain what you observe for the solutions, approximate relative errors, and iterations? Why would we use a whileloop here instead of a forloop as used in Lab 2?

ex=1+x+2!x2+3!x3++n!xn+