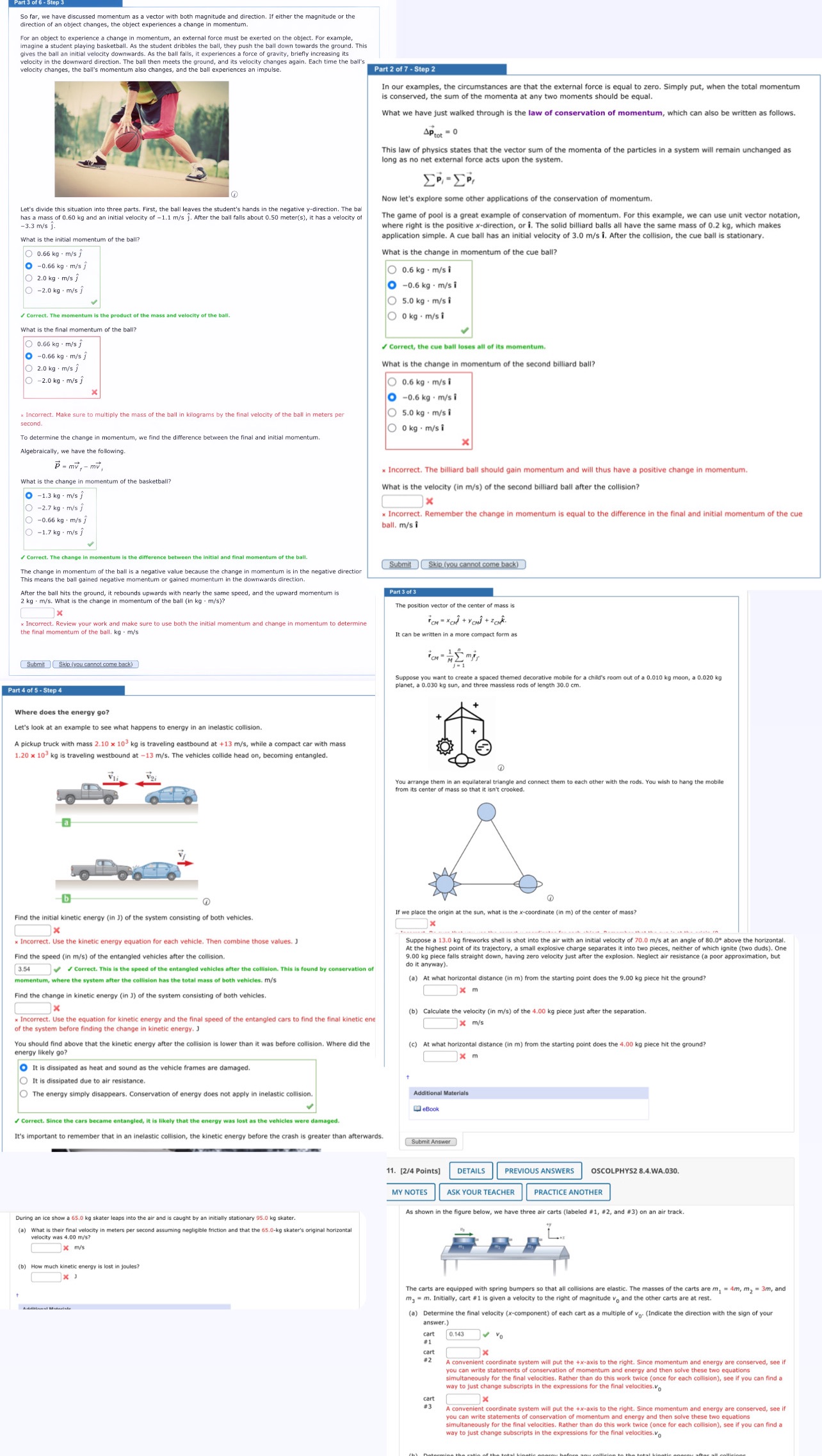
Part 3 of 6 - Step So far, we have discussed momentum as a vector with both magnitude and direction. If either the magnitude or the direction of an object changes, the object experiences a change in momentum. For an object to experience a change in momentum, an external force must be exerted on the object. For example, imagine a student playing basketball. As the student dribbles the ball, they push the ball down towards the ground. This gives the ball an initial velocity downwards. As the ball falls, it experiences a force of gravity, briefly increasing its velocity in the downward direction. The ball then meets the ground, and its velocity changes again. Each time the ball's velocity changes, the ball's momentum also changes, and the ball experiences an impulse. @ Let's divide this situation into three parts. First, the ball leaves the student's hands in the negative y-direction. The bal has a mass of 0.60 kg and an initial velocity of -1.1 m/s j. After the ball falls about 0.50 meter(s), it has a velocity of -3.3 m/s . What is the initial momentum of the ball? O0.66 kg m/s O-0.66 kg m/s O 2.0 kg m/s O -2.0 kg m/s Correct. The momentum is the product of the mass and velocity of the ball. What is the final momentum of the ball? O 0.66 kg - m/s O-0.66 kg m/s O 2.0 kg m/s O-2.0 kg m/s Part 2 of 7-Step 2 In our examples, the circumstances are that the external force is equal to zero. Simply put, when the total momentum is conserved, the sum of the momenta at any two moments should be equal. What we have just walked through is the law of conservation of momentum, which can also be written as follows. AP tot =0 This law of physics states that the vector sum of the momenta of the particles in a system will remain unchanged as long as no net external force acts upon the system. Now let's explore some other applications of the conservation of momentum.. The game of pool is a great example of conservation of momentum. For this example, we can use unit vector notation, where right is the positive x-direction, or i. The solid billiard balls all have the same mass of 0.2 kg, which makes application simple. A cue ball has an initial velocity of 3.0 m/s i. After the collision, the cue ball is stationary. What is the change in momentum of the cue ball? O 0.6 kg m/s i O-0.6 kg m/s i O 5.0 kg m/s i O0 kg m/s i * Incorrect. Make sure to multiply the mass of the ball in kilograms by the final velocity of the ball in meters per second. To determine the change in momentum, we find the difference between the final and initial momentum. Algebraically, we have the following. P = mv,- mv, What is the change in momentum of the basketball? -1.3 kg m/s O -2.7 kg m/s O-0.66 kg m/s O-1.7 kg m/s Correct, the cue ball loses all of its momentum. What is the change in momentum of the second billiard ball? O 0.6 kg m/s i O-0.6 kg m/si 5.0 kg m/s i O0 kg m/si x Incorrect. The billiard ball should gain momentum and will thus have a positive change in momentum. What is the velocity (in m/s) of the second billiard ball after the collision? x Incorrect. Remember the change in momentum is equal to the difference in the final and initial momentum of the cue ball. m/s i x Correct. The change in momentum is the difference between the initial and final momentum of the ball. The change in momentum of the ball is a negative value because the change in momentum is in the negative direction This means the ball gained negative momentum or gained momentum in the downwards direction. After the ball hits the ground, it rebounds upwards with nearly the same speed, and the upward momentum is 2 kg m/s. What is the change in momentum of the ball (in kg m/s)? Submit Skip (you cannot come back) Part 3 of 3 x Incorrect. Review your work and make sure to use both the initial momentum and change in momentum to determine the final momentum of the ball. kg m/s The position vector of the center of mass is It can be written in a more compact form as Submit Skip (you cannot come back) Part 4 of 5-Step 4 Where does the energy go? Let's look at an example to see what happens to energy in an inelastic collision. A pickup truck with mass 2.10 x 103 kg is traveling eastbound at +13 m/s, while a compact car with mass 1.20 x 103 kg is traveling westbound at -13 m/s. The vehicles collide head on, becoming entangled. Vi Voi Find the initial kinetic energy (in 3) of the system consisting of both vehicles. x x Incorrect. Use the kinetic energy equation for each vehicle. Then combine those values. J Find the speed (in m/s) the entangled vehicles after the collision. 3.54 Correct. This is the speed of the entangled vehicles after the collision. This is found conservation of momentum, where the system after the collision has the total mass of both vehicles. m/s -1 Suppose y I want to create a spaced themed decorative mobile for a child's room out of a 0.010 kg moon, a 0.020 kg planet, a 0.030 kg sun, and three massless rods length 30.0 cm. C You arrange them in an equilateral triangle and connect them to each other with the rods. You wish to hang the mobile from its center of mass so that it isn't crooked. If we place the origin at the sun, what is the x-coordinate (in m) of the center of mass? x Suppose a 13.0 kg fireworks shell is shot into the air with an initial velocity of 70.0 m/s at an angle of 80.0 above the horizontal. At the highest point of its trajectory, a small explosive charge separates it into two pieces, neither of which ignite (two duds). One 9.00 kg piece falls straight down, having zero velocity just after the explosion. Neglect air resistance (a poor approximation, but do it anyway). (a) At what horizontal distance (in m) from the starting point does the 9.00 kg piece hit the ground? xm Find the change in kinetic energy (in J) of the system consisting of both vehicles. x Incorrect. Use the equation for kinetic energy and the final speed of the entangled cars to find the final kinetic ene of the system before finding the change in kinetic energy. J You should find above that the kinetic energy after the collision. I lower than it was before collision. Where did the energy likely go? O It is dissipated as heat and sound as the vehicle frames are damaged. O It is dissipated due to air resistance. O The energy simply disappears. Conservation of energy does not apply in inelastic collision. (b) Calculate the velocity (in m/s) of the 4.00 kg piece just after the separation. x m/s (c) At what horizontal distance (in m) from the starting point does the 4.00 kg piece hit the ground? x m Additional Materials eBook Correct. Since the cars became entangled, it is likely that the energy was lost as the vehicles were damaged. It's important to remember that in an inelastic collision, the kinetic energy before the crash is greater than afterwards. Submit Answer During an ice show a 65.0 kg skater leaps into the air and is caught an initially stationary 95.0 kg skater. (a) What is their final velocity in meters per second assuming negligible friction and that the 65.0-kg skater's original horizontal velocity was 4.00 m/s? x m/s 11. [2/4 Points] DETAILS PREVIOUS ANSWERS MY NOTES ASK YOUR TEACHER OSCOLPHYS2 8.4.WA.030. PRACTICE ANOTHER As shown in the figure below, we have three air carts (labeled #1, #2, and #3) on an air track. + (b) How much kinetic energy is lost in joules? x J Additional Motors The carts are equipped with spring bumpers so that all collisions are elastic. The masses of the carts are m = 4m, m = 3m, and m3 m. Initially, cart #1 is given a velocity to the right of magnitude v and the other carts are at rest. (a) Determine the final velocity (x-component) of each cart as a multiple of Vo. (Indicate the direction with the sign of your answer.) cart #1 cart #2 cart #3 0.143 x A convenient coordinate system will put the +x-axis to the right. Since momentum and energy are conserved, see if you can write statements of conservation of momentum and energy and then solve these two equations. simultaneously for the final velocities. Rather than do this work twice (once for each collision), see if you can find a way to just change subscripts in the expressions for the final velocities.vo x A convenient coordinate system will put the +x-axis to the right. Since momentum and energy are conserved, see if you can write statements of conservation of momentum and energy and then solve these two equations simultaneously for the final velocities. Rather than do this work twice (once for each collision), see if you can find a way to just change subscripts in the expressions for the final velocities.Vo