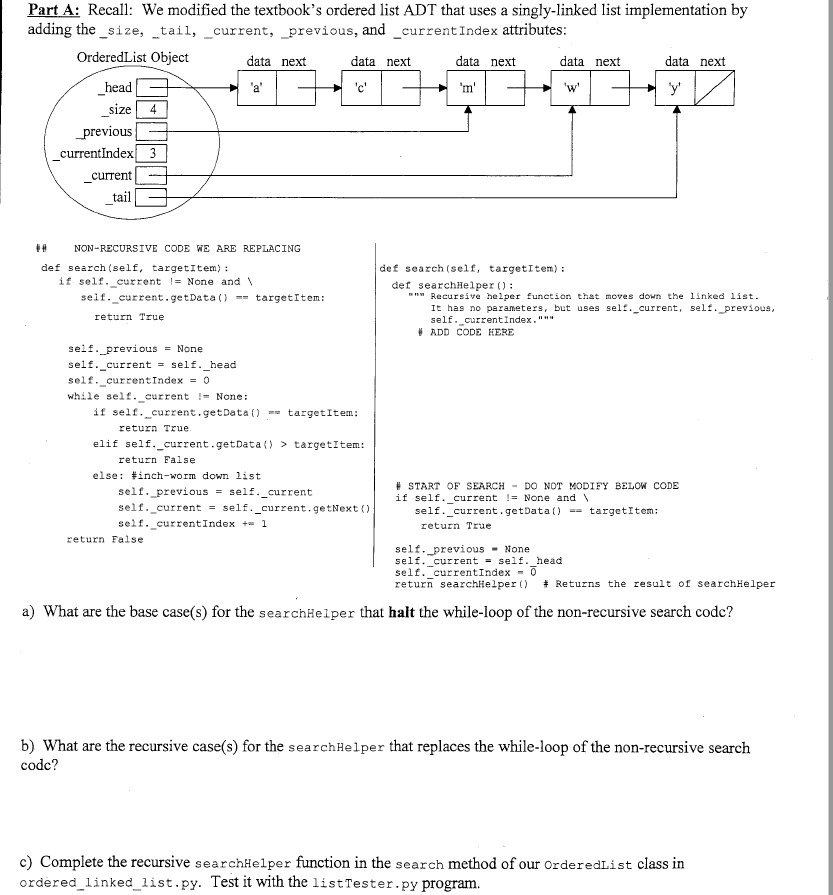
Part A: Recall: We modified the textbook's ordered list ADT that uses a singly-linked list implementation by adding the_size, _tail, _current, _previous, and_currentIndex attributes OrderedList Object data next data next data next data next data next head 'm size4 previous currentIndex 3 current tail NON-RECURSIVE CODE WE ARE REPLACING def search(self, targetitem) def search (self, targetItem) if self- current != None and \ def searchHelper elf._current.getData)targetItem: Recursive helper function that moves down the linked list It has no paraneters, but uses self._current, self._previous self. currentIndex.""" return True ADD CODE HERE self._previous None self, current= self- head self, current!ndex = 0 while self- current !-None ; if self. current.getData)targetItem: elif self._current.getData) > targetItem: else: #inch-worm down list return True return False # START OF SEARCH - DO NOT MODIFY BELO' CODE if self. current-None and self._previous-self._current self._currentself._current.getNext) self. currentIndex1 self._current.getDatal) - targetitem: return True return False self. previousNone self._currentself._head self. currentIndex0 return searchHelper() # Returns the result of searchHelper a) What are the base case(s) for the searchRelper that halt the while-loop of the non-recursive search codc? b) What are the recursive case(s) for the searchHelper that replaces the while-loop of the non-recursive search codc? c) Complete the recursive searchHelper function in the search method of our OrderedList class in ordered_linked list.py. Test it with the 1istTester.py program. Part B: Recall that Lecture 7 and Section 6.6 discussed a very "non-intuitive", but powerful list/array-based approach to implement a priority queue, call a binary heap. The list/array is used to store a complete binary tree a full tree with any additional leaves as far left as possible) with the items being arranges by heap-order property, i.e., each node is S either of its children. An example of a min heap "viewed" an a complete binary tree would be 12] 15 10 20 20 50 10 300 125 Python List actually used to store heap items es50 114 20 20 5o 300 125 117 0 23 4 56 7 89 10 6 | 15 | 10 | 114 | 20 | 20 | 50 | 300 | 125 | 117 Recall the General Idea ofinsert (newItem): append newltem to the end of the list (easy to do, but violates heap-order property) restore the heap-order property by repeatedly swapping the newltem with its parent until it percolates up to the correct spot Recall the General Idea of delMin): remember the minimum value so it can be returned later (easy to find - at index 1) copy the last item in the list to the root, delete it from the right end, decrement size restore the heap-order property by repeatedly swapping this item with its smallest child until it percolates down to the correct spot .return the minimum value Originally, we used iteration (i.e., a loop) to percolate up (see percUp) and percolate down (see percDown) the tree. (textbook code below) NON-RECURSIVE CODE WE ARE REPLACING def percUp(self,i): def pereDown (self,i while 2} 0: mc-self.minChild(i) if self.heapList[i >self.heapList[mc] if self.heapList[] tmpself.heapListi 11 2 self.heapL st { // 2] -self.heapL st [i] self.heapList[] = tmp