Part A

Suppose a rocket is being launched into outer space. On its way up, several different forces act on the rocket. One of these forces, thrust, is applied by the rocket's engines.

The rocket's engines apply a constant upward force to a rocket on its way to outer space. In the absence of other forces, the upward force on the rocket would cause it to accelerate up at a constant rate of a meters/second².

Still ignoring any other forces, the height of the rocket can be expressed as a function of the time elapsed in seconds after the launch, t. This function, f(t), is equal to half the product of the rocket's acceleration and the square of the time after launch. Write the equation for f(t).

Part B

The function f(t) represents how the rocket would move if only the upward force of thrust acted on it. Sketch the graph of f(t) on the axes. Keep in mind that acceleration, a, is a positive constant. Also consider the domain restrictions on time, t.

Part C

The force provided by the rocket's engines is not the only force that acts on the rocket, however. The force of gravity also acts on the rocket. This force results in the downward acceleration of the rocket at a constant rate of g. A second function, G(t), can be written to describe the height of the rocket if gravity were the only force acting on it.

Considering your response to part B and your knowledge of functions, write the equation of G(t). You may want to conduct online research to identify the kinematic equation for the displacement of an object under constant acceleration. Keep in mind that the rocket starts at rest.

After writing your equation, explain how you arrived at your answer.

Part D

The function G(t) represents how the rocket would move if only gravity acted on it. Sketch the graph of G(t) on the axes below. Keep in mind that acceleration due to gravity, g, is a negative constant. Also consider the domain restrictions on time, t.

Part E

Considering factors such as domain, range, location of a vertex, increasing and decreasing intervals, and the shape of the curve, describe any similarities between the graphs of f(x) and G(x). Are there any differences between the two graphs? If so, explain them.

Part F

A third force, drag, also acts on the rocket. This force varies with height and, accordingly, with the time elapsed in seconds after the rocket is launched. Drag also depends on the speed of the rocket, its shape, and its altitude.

Ignoring the other forces, suppose the function d(t) represents the height of the rocket while experiencing drag:

d(t)=-2,500/t+2+1,250

Now let's take all three forces acting on the rocket into account. Suppose that the acceleration due to the rocket's engines, a, is equal to 200 meters/second² and the acceleration due to gravity, g, is equal to -10 meters/second². Write a function, h(t), that represents the height of the rocket as a function of time while experiencing the forces of gravity, drag, and the thrust from the rocket's engines.

Part G

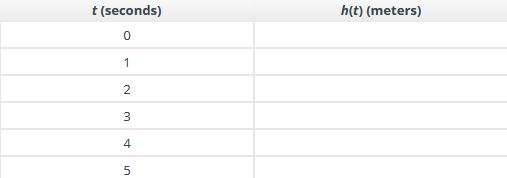
Fill in the table with the appropriate values of h(t) for the given values of t. Round each value to the nearest 10 meters.

(Image of table included)

y 5,000 4,000 3,000 Height (meters) 2,000 1,000 0+ 0 2 3 4 Time (seconds)t (seconds) h(t) (meters) 0 1 2 3 4