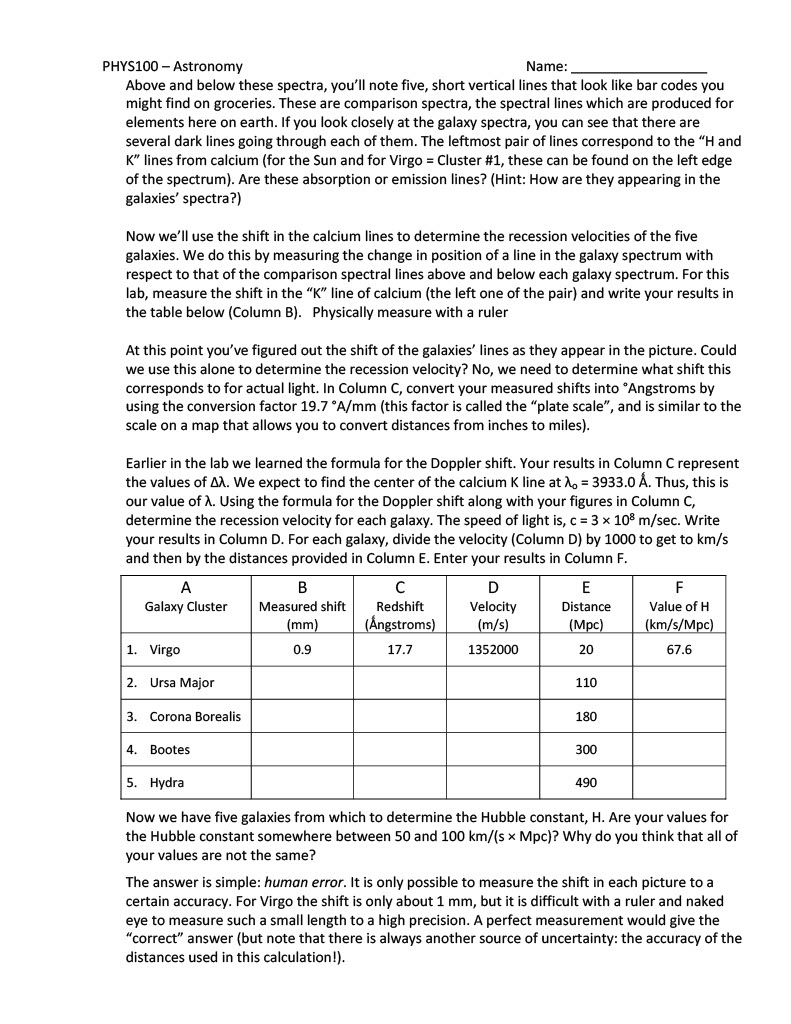
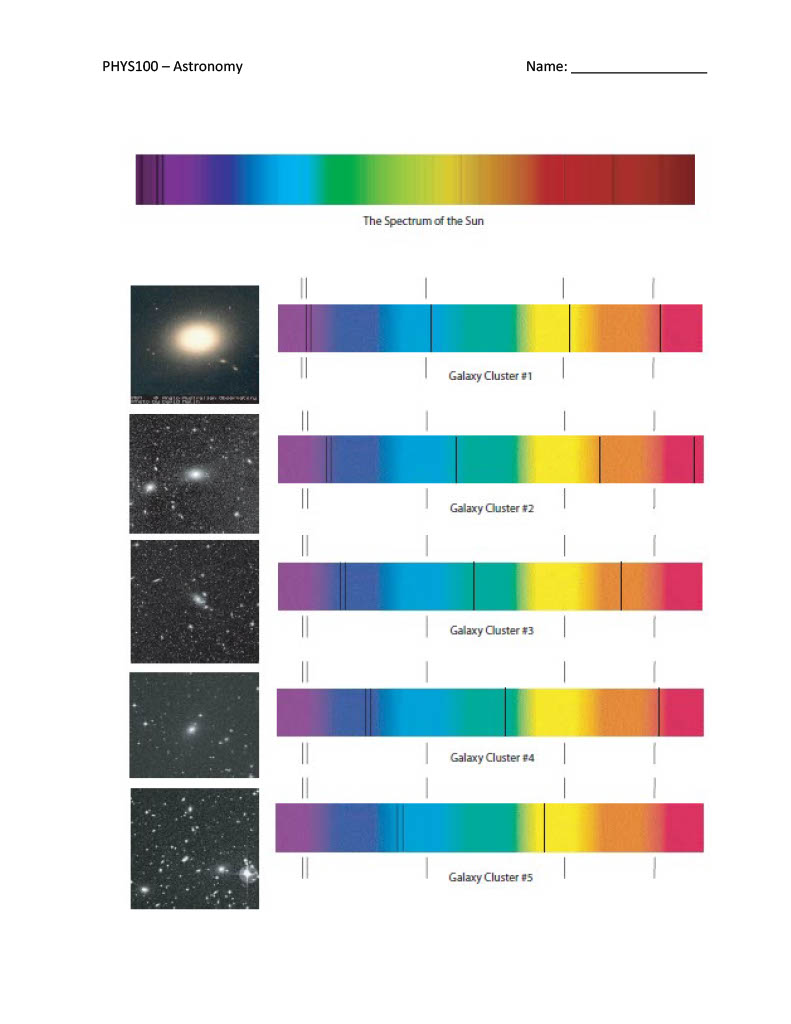
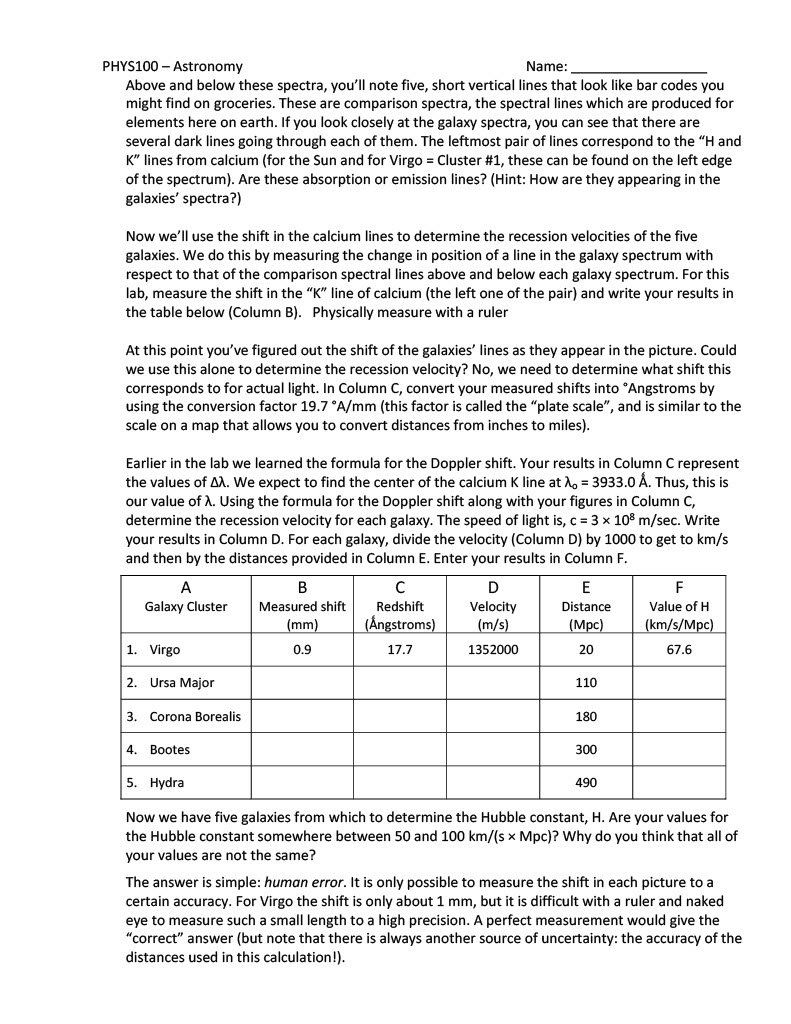
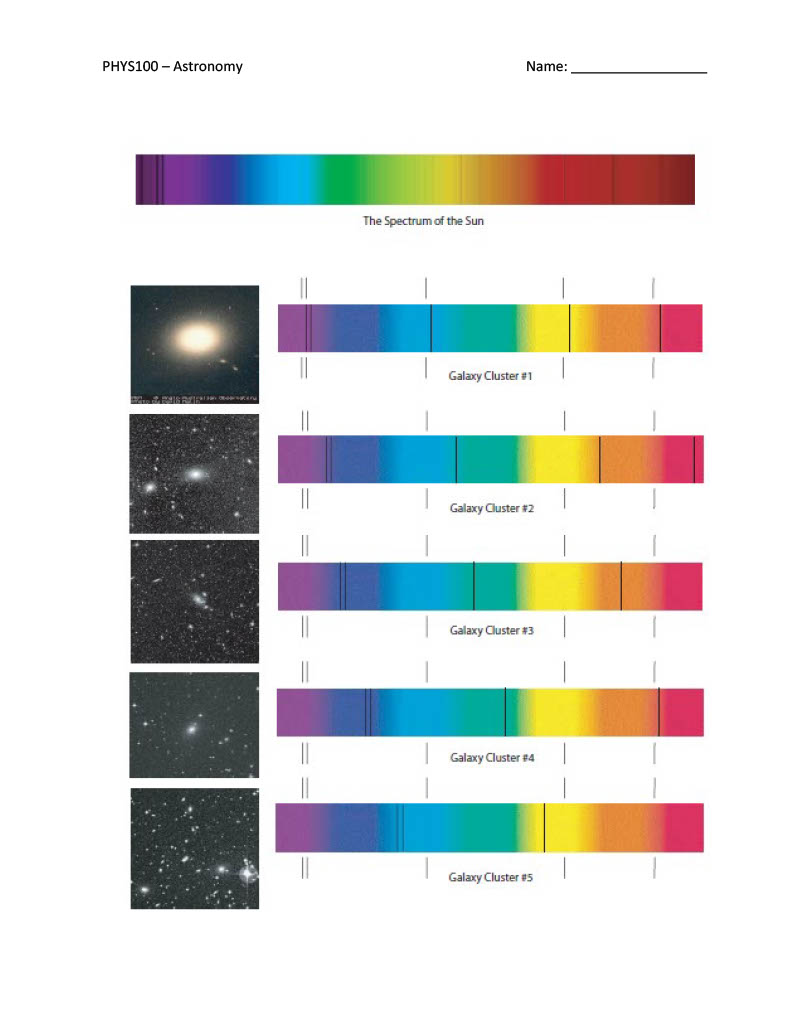
PHY5100 - Astronomy Mame: Lab 11 - Hubble's Law Finding the Age of the Universe Introduction An object's spectrum can be used to determine the temperature and chemical composition of that object. A spectrum can also be used to find out how fast an object is moving by measuring the Doppler shift. In this lab you will learn how the velocity of an object can be found from its spectrum, and how Hubble's Law uses the Doppler shift to determine the distance scale of the Universe. Purpose: To use Doppler Shift and Hubble's Law to determine the age of the Universe. Procedure/Analysis: Part 1: Doppler Shi You have probably noticed that when an ambulance passes by you, the sound of its siren changes. As it approaches, you hear a high, whining sound which switches to a deeper sound as it passes by. This change in pitch is referred to as the Doppler shift. To understand what is happening, let's consider a waterbug treading water in a pond. The bug's kicking legs are making waves in the water. The bug is moving forward relative to the water, so the waves in front of him get compressed, and the waves behind him get stretched out. In other words, the frequency of waves increases in front of him, and decreases behind him. In wavelength terms, the wavelength is shorter in front of him, and longer behind him. Sound also travels in waves, so when the ambulance is approaching you, the frequency is shifted higher, so the pitch (not the volume) is higher. After it has passed you, the frequency is Doppler shifted to a lower pitch as the ambulance moves away from you. You hear the pitch change because to your point of view the relative motion of the ambulance has changed. First it was moving toward you, then away from you. The ambulance driver won't hear any change in pitch, because for her the relative motion of the ambulance hasn't changed. The same thing applies to light waves. When a light source is moving away from you, its wavelength is longer, or the color of the light moves toward the red end of the spectrum. A light source moving toward you shows a (color) shift. This means that we can tell if an object is moving toward or away from us by looking at the change in its spectrum. In astronomy we do this by measuring the wavelengths of spectral lines. We've already learned how each element has a unique fingerprint of spectral lines, so if we look for this fingerprint and notice it is displaced slightly from where we expect it to be, we know that the source must be moving to produce this displacement. We can find out how fast the object is moving by using the Doppler shift formula: .':ulb- d | = I ol PHY5100 - Astronomy Mame: where Al is the wavelength shift you measure, A, is the rest wavelength (the one you'd expect to find if the source wasn't moving), v is the radial velocity (velocity toward or away from us), and c is the speed of light (3 x 10 m/s). In order to do this, you just take the spectrum of your object and compare the wavelengths of the lines you see with the rest wavelengths of lines that you know should be there. For example, we would expect to see lines associated with hydrogen so we might use this set of lines to determine the motion of an object. Here is an example: 1. If we look at the spectrum of a star, we know that there will probably be hydrogen lines. We also know that one hydrogen line always appears at 6563A, but we find the line in the star's spectrum at 6570A. {ngstmms is a unit of length. 1.0 A = 1.0 x 10 m. You can leave the unit in I\\} Let's calculate the Doppler shift: a. First, is the spectrum of the star redshifted or blueshifted (do we observe a longer or shorter wavelength than we would expect)? b. Calculate the wavelength shift (AA). c. What is the radial velocity? (Use the Doppler shift formula) A way to check your answer is to look at the sign of the velocity. Positive means redshift, and negative means blueshift. Einstein told us that nothing can go faster than the speed of light. If you have a very high velocity object moving at close to the speed of light, this formula would give you a velocity faster than light! Consequently, this formula is not always correct. For very high velocities you need to use a different formula, the relativistic Doppler shift formula, but in this lab we won't need it. Part 2: Hubble's Law In the 1920's Hubble and Slipher found that there is a relationship between the redshifts of galaxies and how far away they are (don't confuse this with the ways we find distances to stars, which are much closer). This means that the further away a galaxy is, the faster it is moving away from us. This seems like a strange idea, but it makes sense if the Universe is expanding. The relation between redshift and distance turns out to be very fortunate for astronomers, because it provides a way to find the distances to far away galaxies. The formula we use is known as Hubble's Law: v=H,xd where v is the radial velocity, d is the distance (in Mpc), and Has is called the Hubble constant and is expressed in units of km/(s x Mpc). Hubble's constant is basically the expansion rate of the Universe. The problem with this formula is that the precise value of Hg isn't known! If we take galaxies of known distance and try to find Ho, the values range from 50 to 100 km/(s x Mpc). By using the incredible power of the Hubble Space Telescope, the current value of the Hg is near 75 km/(s x Mpc). Let's do an example illustrating how astronomers are trying to determine He. 2. Determine a value of the Hubble constant based on direct measurements. The figure at the end of this lab has spectra from five different galaxy clusters. At the top of this figure is the spectrum of the Sun for comparison. For each cluster, the spectrum of the brightest galaxy in the cluster is shown to the right of the image of the cluster (usually dominated by a single, bright galaxy). PHY5100 - Astronomy Mame: Above and below these spectra, you'll note five, short vertical lines that look like bar codes you might find on groceries. These are comparison spectra, the spectral lines which are produced for elements here on earth. If you look closely at the galaxy spectra, you can see that there are several dark lines going through each of them. The leftmost pair of lines correspond to the \"H and K" lines from calcium (for the Sun and for Virgo = Cluster #1, these can be found on the left edge of the spectrum). Are these absorption or emission lines? (Hint: How are they appearing in the galaxies' spectra?) MNow we'll use the shift in the calcium lines to determine the recession velocities of the five galaxies. We do this by measuring the change in position of a line in the galaxy spectrum with respect to that of the comparison spectral lines above and below each galaxy spectrum. For this lab, measure the shift in the \"K\" line of calcium (the left one of the pair) and write your results in the table below {Column B). Physically measure with a ruler At this point you've figured out the shift of the galaxies' lines as they appear in the picture. Could we use this alone to determine the recession velocity? No, we need to determine what shift this corresponds to for actual light. In Column C, convert your measured shifts into *Angstroms by using the conversion factor 19.7 *A/mm (this factor is called the \"plate scale\PHY5100 - Astronomy Mame: Part 3: The Age of the Universe The expansion of the Universe is a result of the Big Bang. Since everything is flying apart, it stands to reason that in the past everything was much closer together. With this idea, we can use the expansion rate to determine how long things have been expanding - in other words, the age of the Universe. As an example, suppose you got in your car and started driving down to Eau Claire. Somewhere around Spooner, you look at your watch and wonder what time you left Superior. You know you've driven about 75 miles and have been going 75 miles per hour, so you easily determine you must have left about an hour ago. For the age of the Universe, we essentially do the same thing to figure out how long ago the Universe started. This is assuming that the expansion rate has always been the same, which is probably not true (by analogy, maybe you weren't always driving at 75 mph on your way to Spooner). The gravitational force of the galaxies in the Universe pulling on each other would slow the expansion down. However, we can still use this method to get a rough estimate of the age of the Universe. 3. The Hubble constant is expressed in units of km/(s x Mpc). Since km and Mpc are both units of distance, we can cancel them out and express H in terms of 1/sec. Simply convert the Mpc into km, and cancel the units of distance. The conversion factor is 1 Mpc = 3.086x10% km. a. Add up the five values for the Hubble constant written in the table of #2, and divide the result by five. This represents the average value of the Hubble constant you have determined. b. Conwvert your value of H, into units of 1/s: c. Now convert this into seconds by inverting it (1/Ho from part b): d. How many years is this? (convert from seconds to years by knowing there are 60 seconds in a minute, 60 minutes in an hour, etc.) Part 4: How Do we Measure Distances to Galaxies and Galaxy Clusters? In #2, we made it easy for you by listing the distances to each of the galaxy clusters. If you know the distance to a galaxy, and its redshift, finding the Hubble constant is easy. But how do astronomers find these distances? In fact, it is a very difficult problem. Why? Because the further away an object is from us, the fainter it appears to be. For example, if we were to move the Sun out to a distance of 20 pc, it would no longer be visible to the naked eye! Note that the closest galaxy cluster is at a distance of 20 Mpc, a million times further than this! Even with the largest telescopes in the world, we could not see the Sun at such a great distance (and Virgo is the closest big cluster of galaxies). Think about this question: Why do objects appear to get dimmer with distance? What is actually happening? Answer: The light from a source spreads out as it travels. This is shown in Fig. 1. If you draw (concentric) spheres around a light source, the amount of energy passing through a square meter drops with distance as 1/R%. Why? The area of a sphere is 4nR2. The innermost sphere in Fig. 1 has a radius of \"1\" m, its area is therefore 4nt m2. If the radius of the next sphere out is \"2" m, then its area is 16m mZ. It has 4x the area of the inner sphere. Since all of the light from the light bulb passes through both spheres, its intensity (energy/area) must drop. The higher the intensity, the brighter an object appears to our eyes. The lower the intensity, the fainter it appears. Again, refer to Fig. 1, as shown there, the amount of energy passing through 1 square of the inner sphere passes through 4 squares for the next sphere out, and 9 squares (for R = 3) for the outermost sphere. The light from the light bulb spreads out as it travels, and the intensity drops as 1/R2. PHY5100 - Astronomy Mame: 4, Figure 1: If you draw concentric spheres around a light source [we have cut the spheres in half for clarity), you can see how light spreads out as it travels. The light passing through one sguare on the inner sphere passes through four squares for a sphere that has twice the radius, and nine squares for a sphere that has three times the radius of the Innermost sphere. This Is because the area of a sphere is 4mRZ, If the apparent brightness (or intensity) of an object is proportional to 1/R? (where R = distance), how much brighter is an object in the Virgo cluster, compared to a similar object in Hydra? [Hint: how many times further is Hydra than Virgo?] An object in Hydra is hundreds of times fainter than the same object in Virgo! Obviously, astronomers need to find an object that is very luminous if they are going to measure distances to galaxies that are as far, or even further away than the Hydra cluster. You have probably heard of a supernova. Supernovae (supernovae is the plural of supernova) are tremendous explosions that rip stars apart. There are two types of supernova, Type | is due to the collapse of a white dwarf into neutron star, while a Type Il is the explosion of a massive star that often produces a black hole. Astronomers use Type | supernovae to measure distances since their explosions always release the same amount of energy. Type | supernovae have more than one billion times the Sun's luminosity when they explode! Thus, we can see them a long way. Let's work an example. In 1885 a supernova erupted in the nearby Andromeda galaxy. Andromeda is a spiral galaxy that is similar in size to our Milky Way located at a distance of about 1 Mpc. The 1885 supernova was just barely visible to the naked eye, but would have been easy to see with a small telescope (or even binoculars). Astronomers use telescopes to collect light, and see fainter objects better. The largest telescopes in the world are the Keck telescopes in Hawai. These telescopes have diameters of 10 meters, and collect 6 million times as much light as the naked eye (thus, if you used an eyepiece on a Keck telescope, you could \"see\" objects that are 6 million times fainter than those visible to your naked eye). Using the fact that brightness decreases as 1/R?, how far away (in Mpc) could the Keck telescope see a supernova like the one that blew up in the Andromeda galaxy? [Hint: here we reverse the equation. You are given the brightness ratio, 6 million, and must solve for the distance ratio, remembering that Andromeda has a distance of 1 Mpc!] Could the Keck telescopes see a supernova in Hydra? PHY5100 - Astronomy Mame: Results Questions: 1. Inthe waterbug analogy, we know what happens to waves in front of and behind the bug, but what happens to the waves directly on his left and right (hint: is the bug's motion compressing these waves, stretching them out, or not affecting them at all}? With this in mind, what can the Doppler shift tell us about the motion of a star which is moving only at a right angle to our line of sight? 2. Why did we use an average value for the Hubble constant, determined from five separate galaxies, in our age of the Universe calculation? What other important factor in our determination of the age of the Universe did we overlook? (Hint: It was mentioned in the lab) 3. Does the age of the Universe seem reasonable? Check your textbook or the World Wide Web for the ages estimated for globular clusters, some of the oldest known objects in the Universe. How does our result compare? Can any object in the Universe be older than the Universe itself? Conclusion:; Claim: State a claim addressing the purpose of the lab. (What is the age of the Universe? Evidence: Support your claim with evidence of what you did and/or what you found in the lab. Reason: State any error that you encountered in the lab. State what you could do to reduce this error. Remember to submit your lab report to the Dropbox. PHYS5100 Astronomy Name: The Spectrum of the Sun ! Galaxy Cluster #1 | Galaxy Cluster 2 | Galaxy Cluster #3 | Galaxy Cluster #4 | Galaxy Cluster 85 |