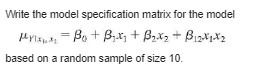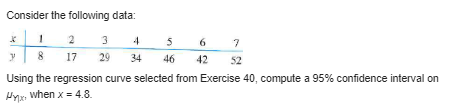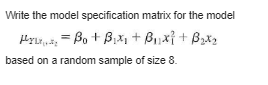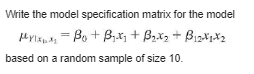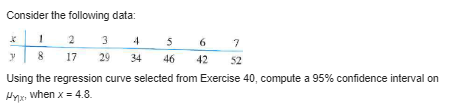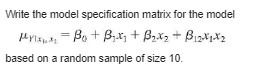







please address all questions:-
Write the model specification matrix for the model Par. =BotBix+ OnxitBox, based on a random sample of size 8.Write the model specification matrix for the model based on a random sample of size 10.2 Let C= - Let Y, and Y, be independent random variables with B[ Y ] = 3, E[Y,] = 9, and Var Y, = Var Y, = 16. (a) Find E[ C]. (b) Find E[CY], where Y = (c) Find Var Y. (d) Find Var CY.Let C= Let Y, and Y, be independent random variables with ETY ] = 5, ETY,] = 10, 7 Var Y, = Var Y, = 6. (a) Find E[CY] where Y = (b) Find Var Y. (c) Find Var CY.Consider the simple linear regression model. Are 8, and B, uncorrelated? Explain, based on the variance-covariance matrix.Consider the model Mrinix = Bot Bit+ B2x2 By definition SSE = ELY, -(Ba + Bix,; + Box27)]2 (a) Square the term on the right and sum over i to obtain SSE = >[Y? - Y(Bo + BX + B2x2) + (Bu + B,xy + Byx2)2- Y,(Bo + Bix + B2x2)] (b) Show that _ [(Bo + Bjxu + Boxy;)2 - Y,(By + Bix, + Byx2)] = Bo (Bo + Bixni + Boxy + Y) + BE ( Boxy + Bx xy + B2x] -x21) (c) Use the normal equations for the multiple linear regression model given in Sec. 12.1 to argue that each of the components on the right of the equation in part (b) is equal to 0. (d) Show that SSE = EY7 - Bo EY, - B Ex Y, - B, ExLY i-1 thus partially verifying the computations used to find SSE.For the simple linear regression model we found that SSE = Sy - BS (See Sec. 11.2. ) In this section we defined SSR for this model by SSR = B Y, + B, S i=1 - Show that B. S= SSR, thus verifying that the results obtained here coincide with those found earlier.The three basic structural elements of a data processing system are files, flows, and processes. Files are collections of permanent records in the system, flows are data interfaces between the system and the environment, and processes are functionally defined logical manipulations of data. An investigation of the cost of developing software as related to files, flows, and processes was investigated. The following data are based on that study. Cost (in units of 1000) Files Flows Processes (v) (IJ) 22.6 44 15.0 33 15 78.1 80 80 28.0 24 21 80.5 50 24.5 18 20.5 41 13 147.6 187 137 4.2 19 15 48.2 50 21 20.5 48 17 Find a 95% confidence interval on Arx,, r, x, when x, = 12, x, = 40, and X, = 20.\fThe three basic structural elements of a data processing system are files, flows, and processes. Files are collections of permanent records in the system, flows are data interfaces between the system and the environment, and processes are functionally defined logical manipulations of data. An investigation of the cost of developing software as related to files, flows, and processes was investigated. The following data are based on that study. Cost (in units of 1000) Files Flows Processes ( v) 22.6 44 18 15.0 33 15 78.1 80 80 28.0 24 21 80.5 227 50 24.5 20 18 20.5 41 13 147.6 187 137 4.2 19 15 48.2 50 21 20.5 48 17 Find a 90% confidence interval on Ap.The three basic structural elements of a data processing system are files, flows, and processes. Files are collections of permanent records in the system, flows are data interfaces between the system and the environment, and processes are functionally defined logical manipulations of data. An investigation of the cost of developing software as related to files, flows, and processes was investigated. The following data are based on that study. Cost (in units of 1000) Files Flows Processes (v) (r , ) (x]) 22.6 44 18 15.0 2 33 15 78.1 80 80 28.0 24 21 80.5 227 50 24.5 20 18 20.5 41 13 147.6 187 137 4.2 19 15 48.2 50 21 20.5 48 17 Find a 90% confidence interval on B.Consider the following data: 2 3 5 6 17 29 34 46 42 52 For the model of Exercise 38, 2.428571 -1.28571 1428571 (XX]= =-1.28571 .797619 -.0952381 .1428571 -.0952381 .01190476 228 X'y = 1111 6091 3 = 12.27380952 Use this information to estimate the model.Consider the following data: 2 3 5 6 17 29 34 46 42 52 Test an appropriate hypothesis to decide whether the quadratic regression curve significantly fits the data better than the linear regression curve.Consider the following data: 2 3 4 5 6 7 17 29 34 46 42 52 Using the regression curve selected from Exercise 40, compute a 95% confidence interval on Pyx, when x = 4.8