Please address the following items using the attached screenshots.Be sure to answer the questions about both confidence intervals and hypothesis testing.

1. In the Python script, you calculated the sample data to construct a 90% and 99% confidence interval for the average diameter of ball bearings produced from this manufacturing process. These confidence intervals were created using the Normal distribution based on the assumption that the population standard deviation is known and the sample size is sufficiently large. Report these confidence intervals rounded to two decimal places. See Step 2 in the Python script.
2. Interpret both confidence intervals. Make sure to be detailed and precise in your interpretation.

It has been claimed from previous studies that the average diameter of ball bearings from this manufacturing process is 2.30 cm. Based on the sample of 50 that you collected, is there evidence to suggest that the average diameter is greater than 2.30 cm? Perform a hypothesis test for the population mean at alpha = 0.01.

In your initial post, address the following items:

1. Define the null and alternative hypothesis for this test in mathematical terms and in words.
2. Report the level of significance.
3. Include the test statistic and the P-value. See Step 3 in the Python script. (Note that Python methods return two tailed P-values. You must report the correct P-value based on the alternative hypothesis.)
4. Provide your conclusion and interpretation of the results. Should the null hypothesis be rejected? Why or why not?

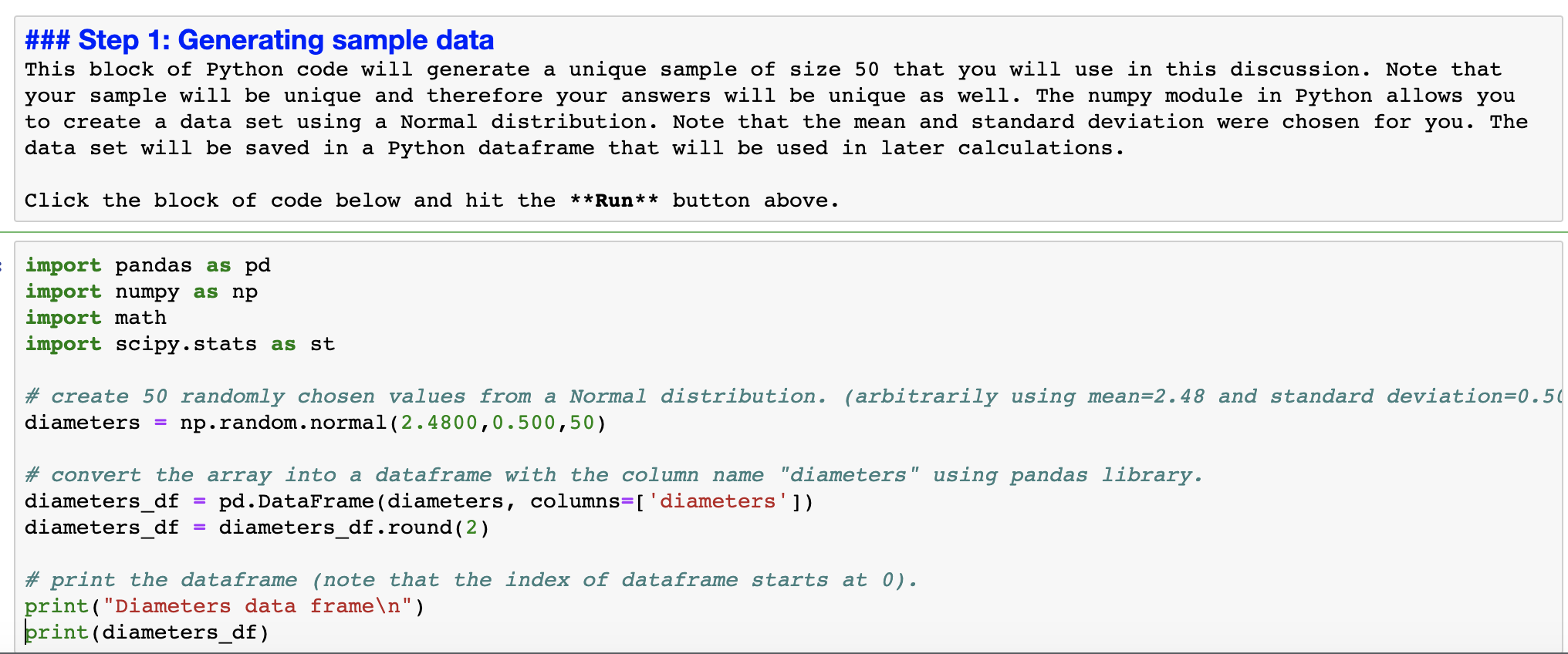
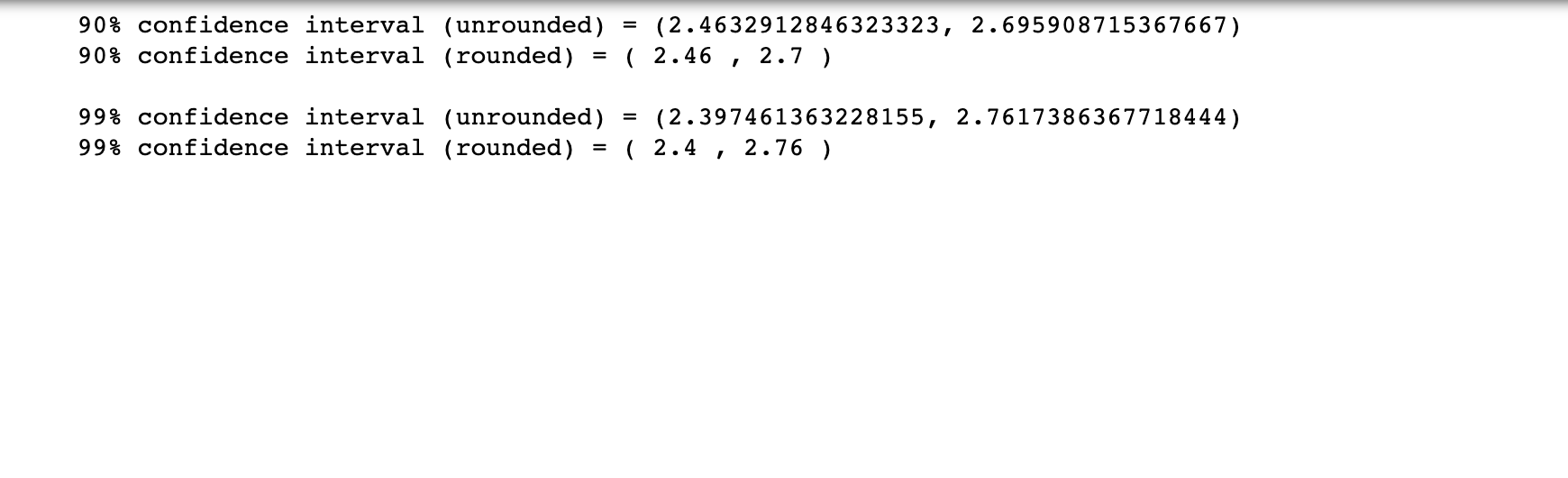
### Step 1: Generating sample data This block of Python code will generate a unique sample of size 50 that you will use in this discussion. Note that your sample will be unique and therefore your answers will be unique as well. The numpy module in Python allows you to create a data set using a Normal distribution. Note that the mean and standard deviation were chosen for you. The data set will be saved in a Python dataframe that will be used in later calculations. Click the block of code below and hit the **Run** button above. import pandas as pd import numpy as up import math import scipy.stats as st # create 50 randomly chosen values from a Normal distribution. (arbitrarily using mean=2.48 and standard deviation=0.5( diameters = np.random.normal(2.4800,0.500,50) # convert the array into a dataframe with the column name "diameters" using pandas library. diameters_df = pd.DataFrame(diameters, columns=['diameters']) diameters_df = diameters_df.round(2) # print the dataframe (note that the index of dataframe starts at 0). print("Diameters data frame\ \") brint(diameters_df) ### Step 2: Constructing confidence intervals You will assume that the population standard deviation is known and that the sample size is sufficiently large. Then you will use the Normal distribution to construct these confidence intervals. You will use the submodule scipy . stats to construct confidence intervals using your sample data. Click the block of code below and hit the **Run* * button above. # Python methods that calculate confidence intervals require the sample mean and the standard error as inputs. # calculate the sample mean mean = diameters_df [ ' diameters' ].mean ( ) # input the population standard deviation, which was given in Step 1. std_deviation = 0.5000 # calculate standard error = standard deviation / sqrt (n) where n is the sample size. stderr = std_deviation/math . sqrt (len (diameters_df [ ' diameters' ]) ) # construct a 908 confidence interval. conf_int_90 = st. norm. interval (0.90, mean, stderr) print ( "90% confidence interval (unrounded) =", conf_int_90) print ( "90% confidence interval (rounded) = (", round(conf_int_90[0], 2), ", ", round (conf_int_90 [1], 2), ")") print (" " ) # construct a 998 confidence interval. conf_int_99 = st. norm. interval(0.99, mean, stderr) print ( "998 confidence interval (unrounded) =", conf_int_99) print( "99% confidence interval (rounded) = (", round(conf_int_99[0], 2), " , " , round (conf_int_99 [1] , 2), ")")\f\f##it Step 3: Performing hypothesis testing for the population mean Since you were given the population standard deviation in Step 1 and the sample size is sufficiently large, you can use the ztest for population means. The z-test method in statsmodels.stats.weightstats submodule runs the ztest. The input to this method is the sample dataframe and the value under the null hypothesis. The output is the test statistic and the twotailed Pvalue. Click the block of code below and hit the **Run** button above. from statsmodels.stats.weightstats import ztest # run z-test hypothesis test for population mean. The value under the null hypothesis is 2.30. test_statistic, p_value = ztest(xl = diameters_df['diameters'], value = 2.30) print("ztest hypothesis test for population mean") print("teststatistic =", round(test_statistic,2)) print("two tailed pvalue =",round(p_value,4)) ztest hypothesis test for population mean teststatistic = 3.29 two tailed pValue = 0.001