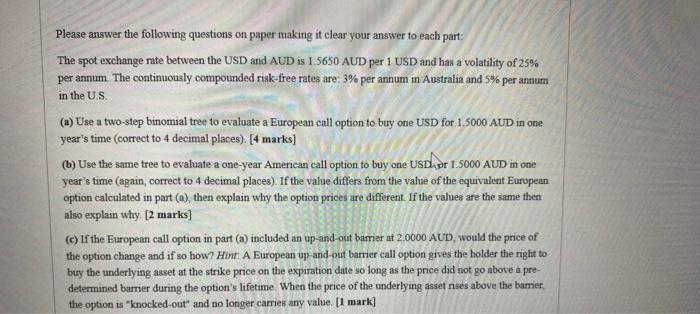
Please answer the following questions on paper making it clear your answer to each part: The spot exchange rate between the USD and AUD is 1.5650 AUD per 1 USD and has a volatility of 25% per annum. The continuously compounded risk-free rates are: 3% per annum in Australia and 5% per annum in the U.S. (a) Use a two-step binomial tree to evaluate a European call option to buy one USD for 1.5000 AUD in one year's time (correct to 4 decimal places). [4 marks] (b) Use the same tree to evaluate a one-year American call option to buy one USDior 1.5000 AUD in one year's time (again, correct to 4 decimal places). If the value differs from the value of the equivalent European option calculated in part (a), then explain why the option prices are different. If the values are the same then also explain why. [2 marks] (c) If the European call option in part (a) included an up-and-out barrier at 2,0000 AUD, would the price of the option change and if so how? Hint A European up-and-out barrier call option gives the holder the right to buy the underlying asset at the strike price on the expiration date so long as the price did not go above a predetermined barrier during the option's lifetime. When the price of the underlying asset nses above the bamier, the option is "knocked-out" and no longer carries any value. [1 mark] Please answer the following questions on paper making it clear your answer to each part: The spot exchange rate between the USD and AUD is 1.5650 AUD per 1 USD and has a volatility of 25% per annum. The continuously compounded risk-free rates are: 3% per annum in Australia and 5% per annum in the U.S. (a) Use a two-step binomial tree to evaluate a European call option to buy one USD for 1.5000 AUD in one year's time (correct to 4 decimal places). [4 marks] (b) Use the same tree to evaluate a one-year American call option to buy one USDior 1.5000 AUD in one year's time (again, correct to 4 decimal places). If the value differs from the value of the equivalent European option calculated in part (a), then explain why the option prices are different. If the values are the same then also explain why. [2 marks] (c) If the European call option in part (a) included an up-and-out barrier at 2,0000 AUD, would the price of the option change and if so how? Hint A European up-and-out barrier call option gives the holder the right to buy the underlying asset at the strike price on the expiration date so long as the price did not go above a predetermined barrier during the option's lifetime. When the price of the underlying asset nses above the bamier, the option is "knocked-out" and no longer carries any value. [1 mark]