Please answer this using MATLAB. The function being used is in the second picture included.
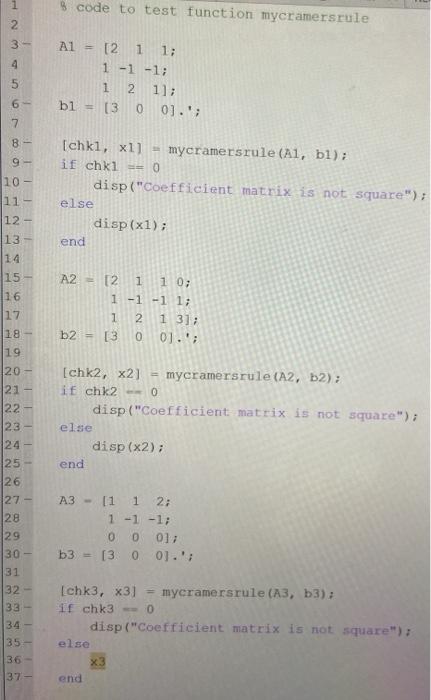
X; = In this exercise, you have to write a function that employs the Cramer's rule to find the solution of a linear system Ax = b with n equations in n unknowns. Recall that the solution is given by det(AD) i = 1,2,...,n (1) det(A) where the matrix A is obtained from the matrix A by replacing its ith column with the constant vector b. The function named mycramersrule should accept two inputs in the specified order: 1. A matrix A representing the coefficient matrix of the linear system. 2. A column vector b representing the constant matrix of the linear system. The function should return two outputs in the specified order: 1. A scalar variable is square, which is a logical value that indicates whether input A is a square matrix (logical 0 for non-square and logical 1 for square matrices) 2. A column vector sol_x. If A is a square matrix with det(A) = 0, then the function should return the solution (as a vector) computed using the Cramer's rule per eq. (1). If A is not a square matrix or if det(A)= 0, then sol_x should be the empty matrix []. Save the script file containing the function definition as mycramersrule.m". Download the file myCramertest.m and make sure that this file is in the same folder as your function definition file. Run the script myCramertest.m to check whether your function definition is performing as desired. You may find the following Matlab commands helpful to compute the solution according to eq. (1).: det, size, ==, for, if-else Note that after ensuring that A is square, we should also check that the variable b is a column vector whose length matches the order n of the square matrix A. However, to keep the complexity of this exercise at a manageable level, we are assuming that this is already true and doesn't need to be verified. 1 % code to test function mycramersrule 2 Al- 4 5 [2 1 1; 1 -1 -1; 1 2 1]; [30 0].'; 6- bl- 7 B- -- Ichki, xl] - mycramersrule (Al, bl); if chki - 0 disp("Coefficient matrix is not square"); else disp(x1); end 9 - 10 11 - 12 - 13 14 15 16 17 18- 19 A2 = 12 1 1 0; 1 -1 -1 1; 1 2 1 31; b2 = 13 0 01.'; 20 - 21 22- 23 124 25 26 27- 28 [chk2, x2] mycramersrule (A2, 2); if chk20 disp ("Coefficient matrix is not square"); else disp (x2); end A3 - [1 1 2; 1-1 -1; 0 0 0]; [30 0].'; 29 30 - b3 31 32 - 33 - 34- 35 36 1 1 1 Ichk3, x31 = mycramersrule (A3, 53); If chk30 disp ("Coefficient matrix is not square"); else x3 end 37 - X; = In this exercise, you have to write a function that employs the Cramer's rule to find the solution of a linear system Ax = b with n equations in n unknowns. Recall that the solution is given by det(AD) i = 1,2,...,n (1) det(A) where the matrix A is obtained from the matrix A by replacing its ith column with the constant vector b. The function named mycramersrule should accept two inputs in the specified order: 1. A matrix A representing the coefficient matrix of the linear system. 2. A column vector b representing the constant matrix of the linear system. The function should return two outputs in the specified order: 1. A scalar variable is square, which is a logical value that indicates whether input A is a square matrix (logical 0 for non-square and logical 1 for square matrices) 2. A column vector sol_x. If A is a square matrix with det(A) = 0, then the function should return the solution (as a vector) computed using the Cramer's rule per eq. (1). If A is not a square matrix or if det(A)= 0, then sol_x should be the empty matrix []. Save the script file containing the function definition as mycramersrule.m". Download the file myCramertest.m and make sure that this file is in the same folder as your function definition file. Run the script myCramertest.m to check whether your function definition is performing as desired. You may find the following Matlab commands helpful to compute the solution according to eq. (1).: det, size, ==, for, if-else Note that after ensuring that A is square, we should also check that the variable b is a column vector whose length matches the order n of the square matrix A. However, to keep the complexity of this exercise at a manageable level, we are assuming that this is already true and doesn't need to be verified. 1 % code to test function mycramersrule 2 Al- 4 5 [2 1 1; 1 -1 -1; 1 2 1]; [30 0].'; 6- bl- 7 B- -- Ichki, xl] - mycramersrule (Al, bl); if chki - 0 disp("Coefficient matrix is not square"); else disp(x1); end 9 - 10 11 - 12 - 13 14 15 16 17 18- 19 A2 = 12 1 1 0; 1 -1 -1 1; 1 2 1 31; b2 = 13 0 01.'; 20 - 21 22- 23 124 25 26 27- 28 [chk2, x2] mycramersrule (A2, 2); if chk20 disp ("Coefficient matrix is not square"); else disp (x2); end A3 - [1 1 2; 1-1 -1; 0 0 0]; [30 0].'; 29 30 - b3 31 32 - 33 - 34- 35 36 1 1 1 Ichk3, x31 = mycramersrule (A3, 53); If chk30 disp ("Coefficient matrix is not square"); else x3 end 37
