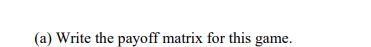Please assist me.
Thank you.
Game theory practice questions;
1. Consider the following two-person game: Player 2 L R Player 1 U 1, 2 0, 1 D 3, 0 x, 1 Assume that both players know the value of x, and both know that they know, and so on. (a) For what values of x (if any) is there a Nash equilibrium in which Player 2 chooses R with probability one? Explain, and describe the equilibrium or equilibria in different cases.(b) For what values of x (if any) does decision R for Player 2 survive iterated deletion of strictly dominated strategies? Explain.2. Two players, Row and Column, are driving toward each other on a one-lane road. Each player chooses simultaneously between going straight (S), swerving left (L), and swerving right (R). If one player goes straight while the other swerves, either right or left, the one who goes straight gets payoff 3 while the other gets -1. If each player swerves to his left, or each swerves to his right, then each gets 0 (remember, they are going in opposite directions). If both go straight, or if one swerves to his left while the other swerves to his right, then the cars crash and each gets payoff -4.\f\f(d) Find a Nash equilibrium in which Row uses a pure strategy and Column mixes between two of his strategies. Clearly identify which strategy or strategies have positive probabilities for each player, and what Column's mixing probabilities are. (Hint: Which of Row's pure strategies could make Column willing to put positive probability on two of Column's pure strategies?)(e) Find a Nash equilibrium in which both Row and Column mix between two of their strategies. Clearly identify which strategies have positive probabilities for each player, and their mixing probabilities are. (Hint: Pick two pure strategies for each player- because the game is symmetric, it's natural to try the same two strategies for each-and figure out what the mixing probabilities would have to be on just those two strategies. Then compare each player's expected payoff with what he could get by switching to his third strategy.)(f) Find the (unique) Nash equilibrium where each player uses all three of his strategies in a mixture. (Hint: First prove that the probabilities of L and R must be equal in the equilibrium mixture. Then show that for each player the probability of S must be 5/8.)3. Suppose three identical, risk-neutral firms must decide simultaneously and irreversibly whether to enter a new market which can accommodate only two of them. If all three firms enter, all get payoff 0; otherwise, entrants get 9 and firms that stay out get 8. (a) Identify the unique mixed-strategy equilibrium and describe the resulting probability distribution of the total ex post number of entrants. (You are not asked to show this, but the game also has three pure-strategy equilibria, in each of which exactly two firms enter; but these equilibria are arguably unattainable in a one-shot game in the absence of prior agreement or precedent. The mixed-strategy equilibrium is symmetric, hence attainable.)