Please calculate the amount of the annual rental payment part b.

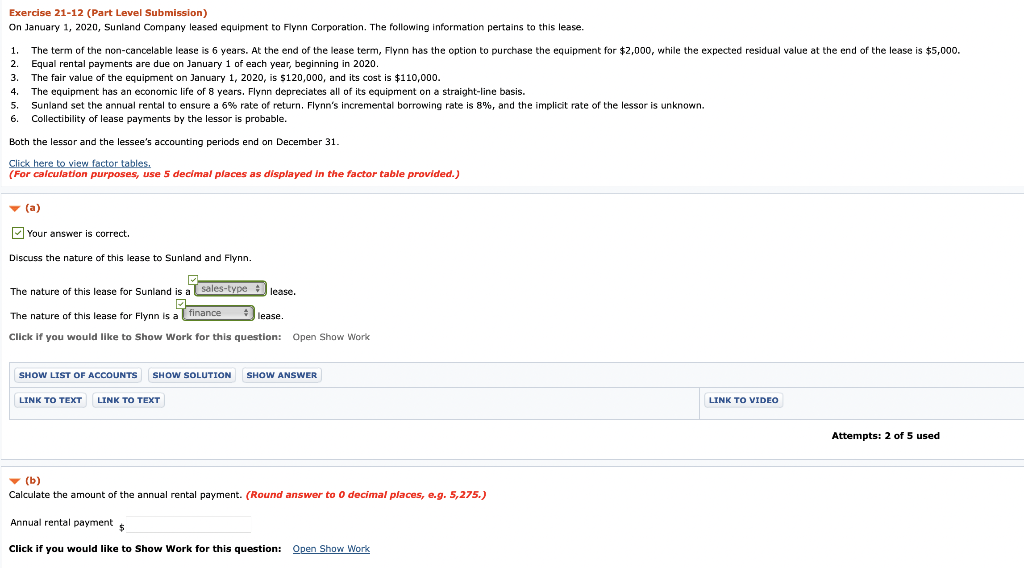
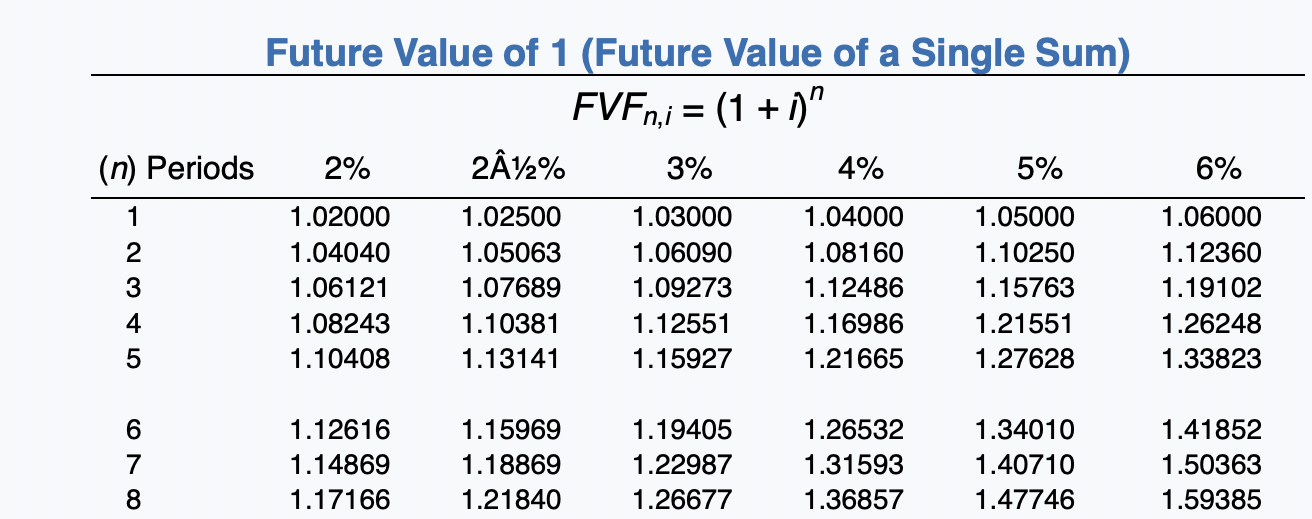
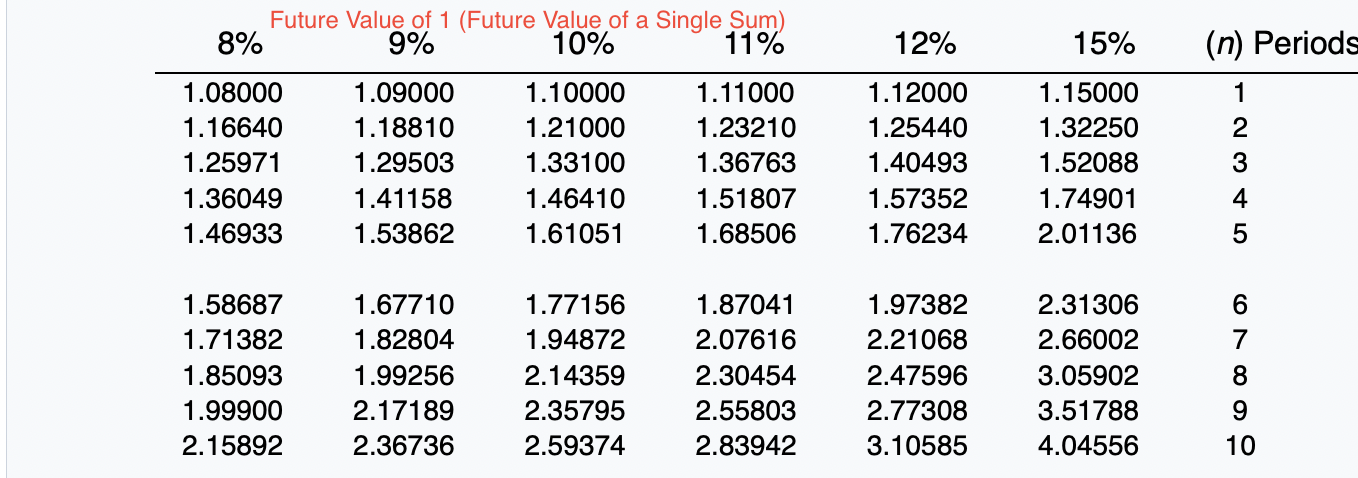
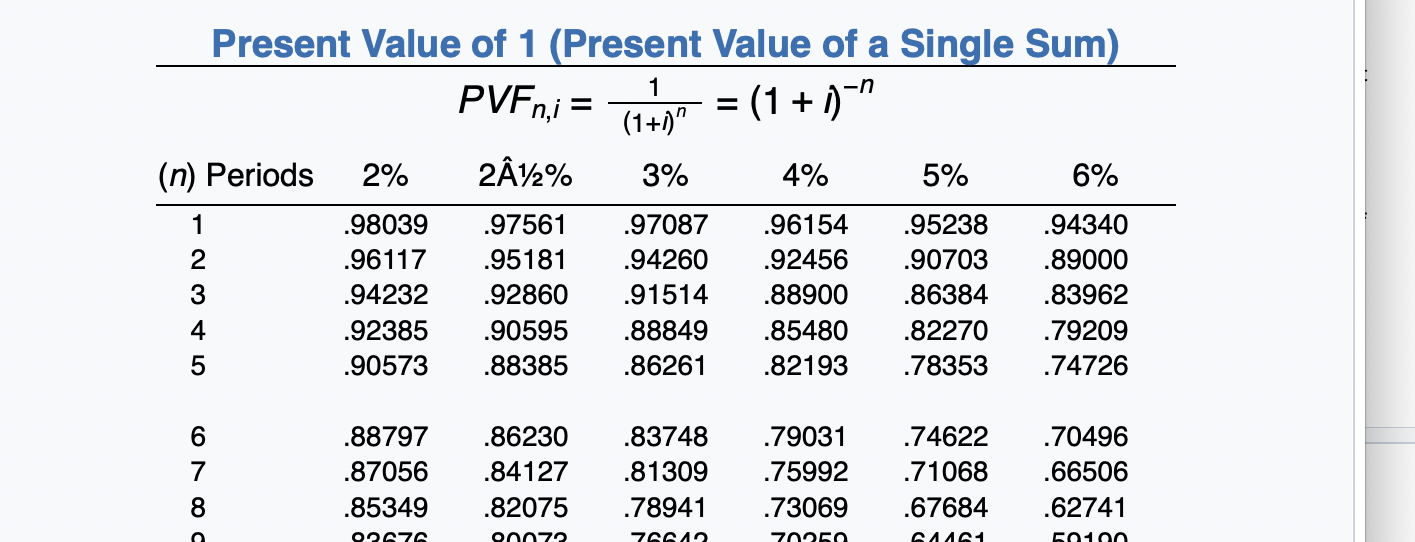
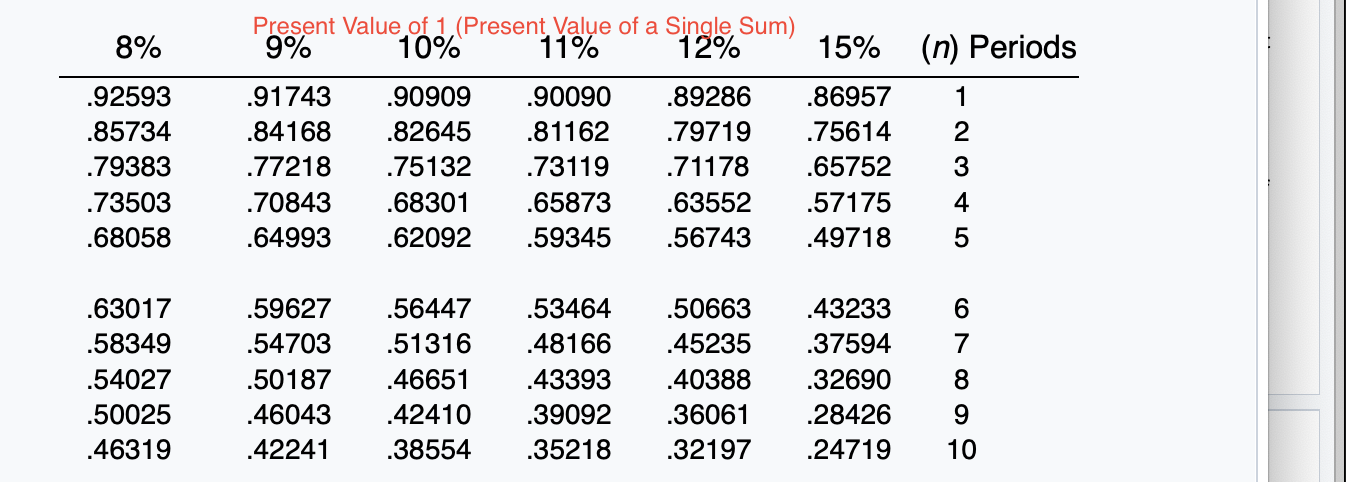
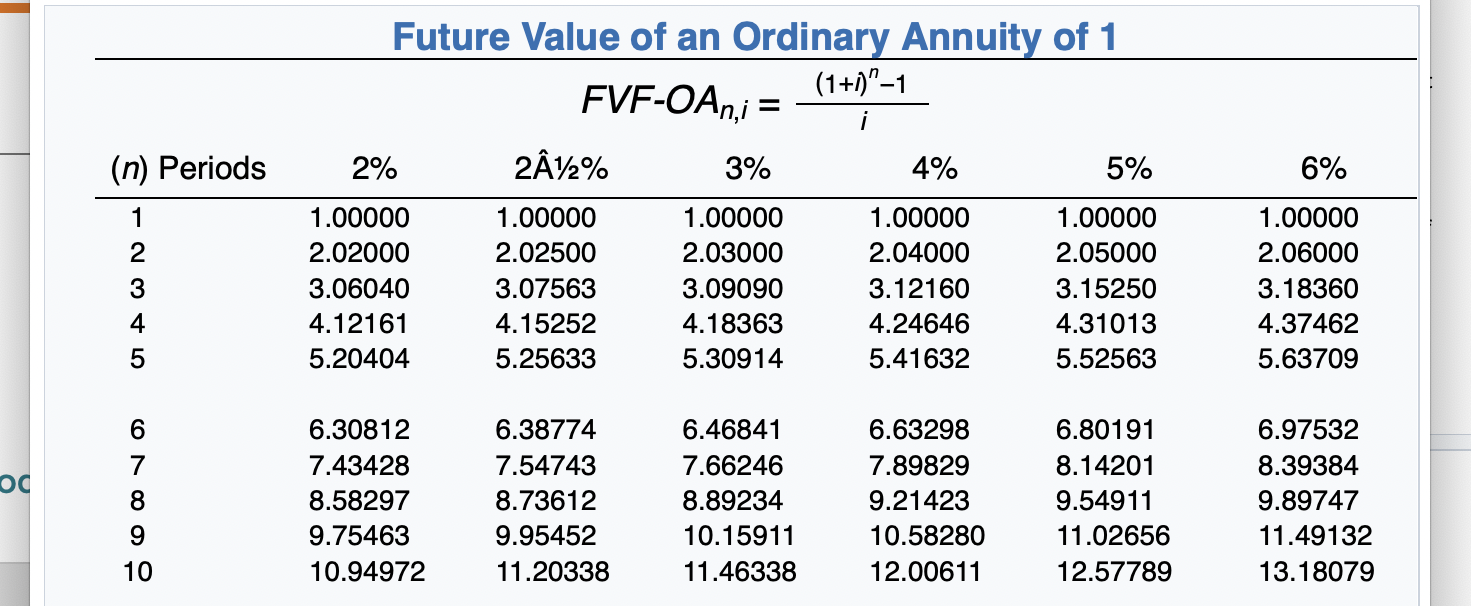
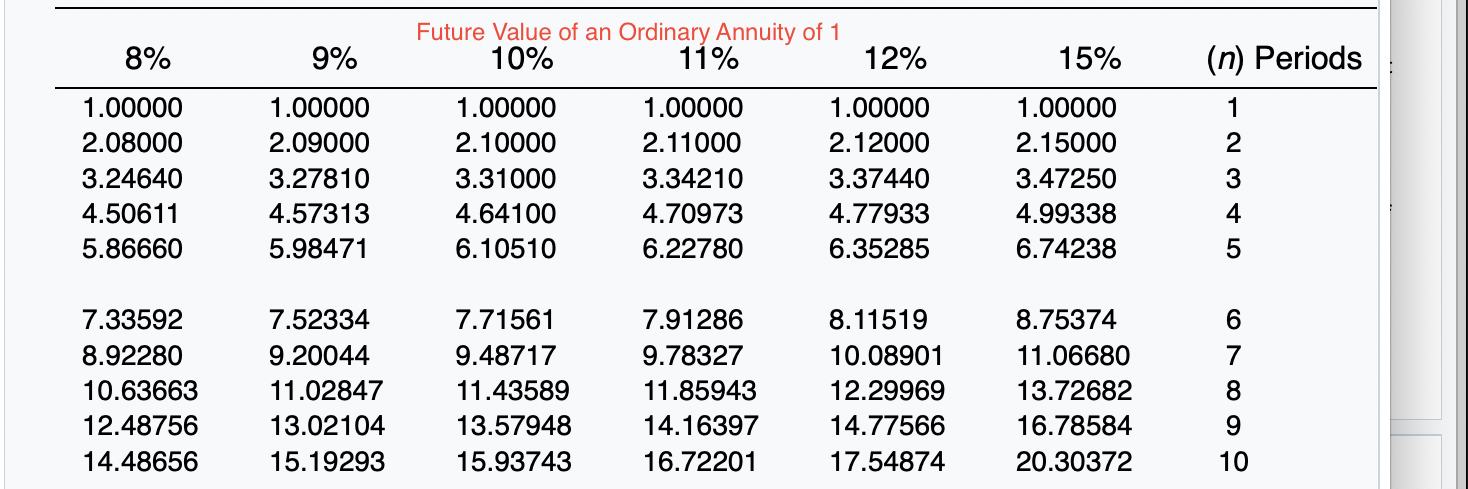
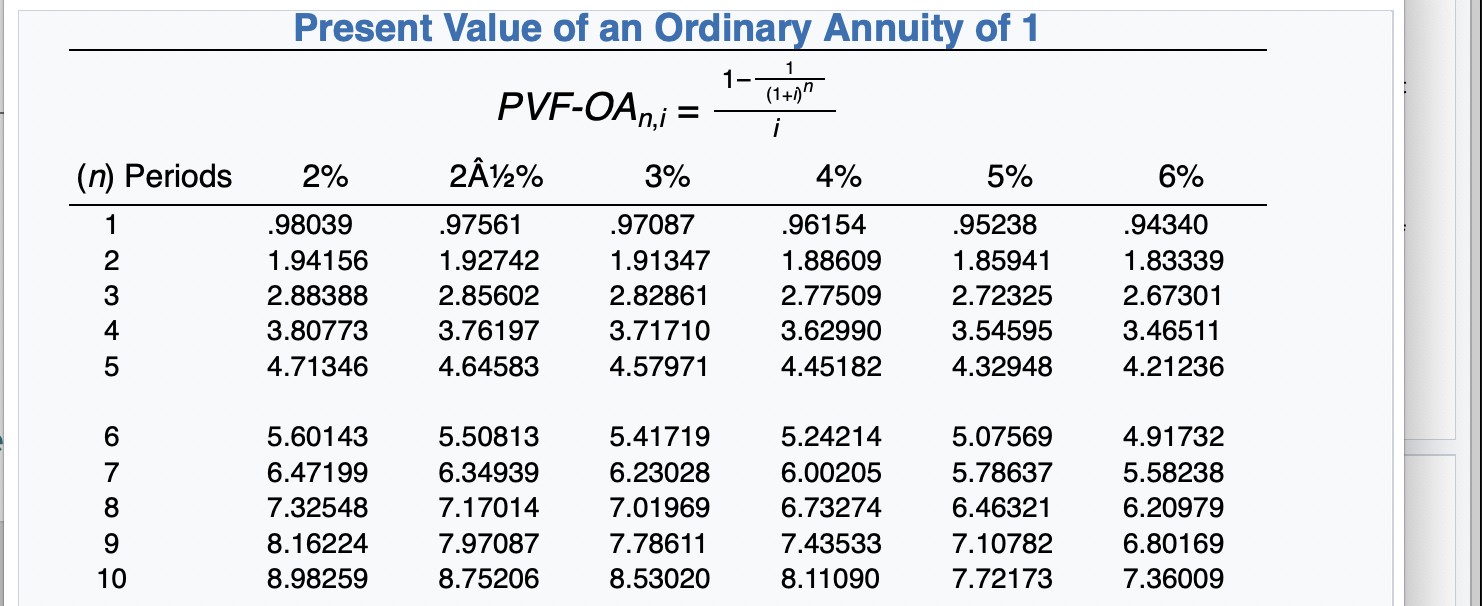
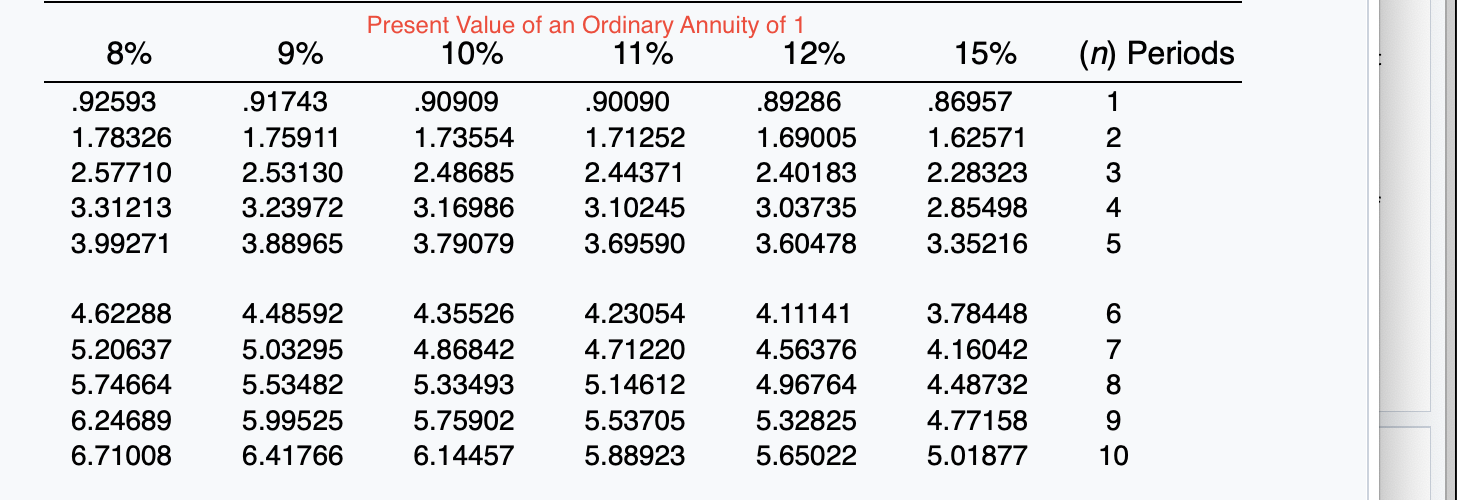
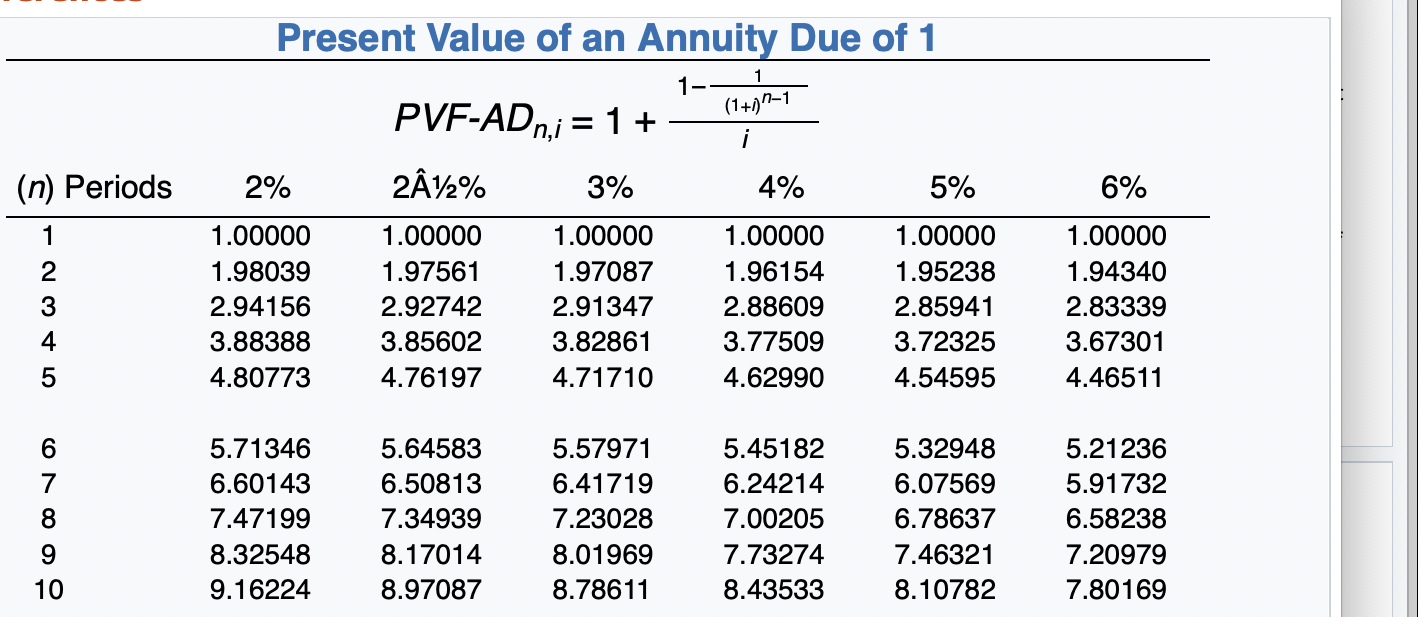
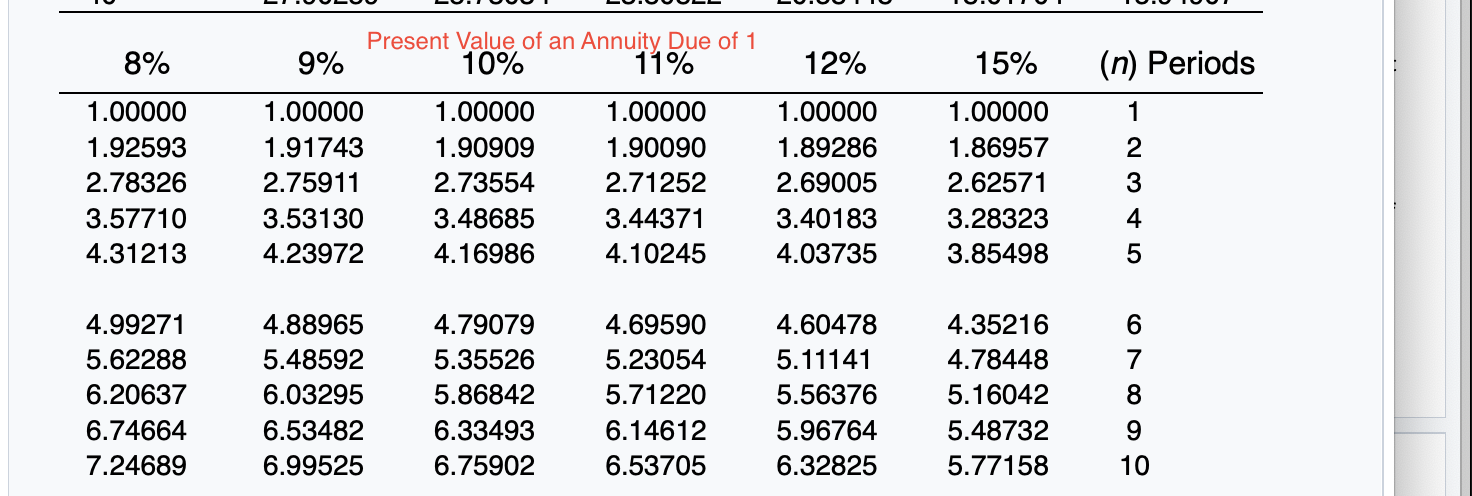
Exercise 21-12 (Part Level Submission) On January 1, 2020, Sunland Company leased equipment to Flynn Corporation. The following information pertains to this lease. 1 The term of the non-cancelable lease is 6 years. At the end of the lease term, Flynn has the option purchase the equipment for $2,000, while the expected residual value at the end of the lease is $5,000. 2 Equal rental payments are due on January 1 of each year, beginning in 2020. 3. The fair value of the equipment on January 1, 2020, is $120,000, and its cost is $110,000. 4. The equipment has an economic life of 8 years. Flynn depreciates all of its equipment on a straight-line basis. 5. Sunland set the annual rental to ensure a 6% rate of return. Flynn's incremental borrowing rate is 8%, and the implicit rate of the lessor is unknown. 6 Collectibility of lease payments by the lessor is probable. Both the lessor and the lessee's accounting periods end on December 31. Click here to view factor tables. (For calculation purposes, use 5 decimal places as displayed in the factor table provided.) (a) Your answer correct. Discuss the nature of this lease to Sunland and Flynn. The nature of this lease for Sunland is a sales-type lease. The nature of this lease for Flynn is a finance lease. Click if you would like to Show Work for this question: Open Show Work SHOW LIST OF ACCOUNTS SHOW SOLUTION SHOW ANSWER LINK TO TEXT LINK TO TEXT LINK TO VIDEO Attempts: 2 of 5 used (b) Calculate the amount of the annual rental payment. (Round answer to 0 decimal places, e.g. 5,275.) Annual rental payments Click if you would like to Show Work for this question: Open Show Work 6% Future Value of 1 (Future Value of a Single Sum) FVFn,i = (1 + i)" (n) Periods 2% 2A%% 3% 4% 5% 1 1.02000 1.02500 1.03000 1.04000 1.05000 2 1.04040 1.05063 1.06090 1.08160 1.10250 3 1.06121 1.07689 1.09273 1.12486 1.15763 4 1.08243 1.10381 1.12551 1.16986 1.21551 5 1.10408 1.13141 1.15927 1.21665 1.27628 1.06000 1.12360 1.19102 1.26248 1.33823 7 8 1.12616 1.14869 1.17166 1.15969 1.18869 1.21840 1.19405 1.22987 1.26677 1.26532 1.31593 1.36857 1.34010 1.40710 1.47746 1.41852 1.50363 1.59385 Future Value of 1 (Future Value of a Single Sum) 8% 9% 10% 11% 12% 15% (n) Periods 1.08000 1.16640 1.25971 1.36049 1.46933 1.09000 1.18810 1.29503 1.41158 1.53862 1.10000 1.21000 1.33100 1.46410 1.61051 1.11000 1.23210 1.36763 1.51807 1.68506 1.12000 1.25440 1.40493 1.57352 1.76234 1.15000 1.32250 1.52088 1.74901 2.01136 1 2 3 4 5 1.58687 1.71382 1.85093 1.99900 2.15892 1.67710 1.82804 1.99256 2.17189 2.36736 1.77156 1.94872 2.14359 2.35795 2.59374 1.87041 2.07616 2.30454 2.55803 2.83942 1.97382 2.21068 2.47596 2.77308 3.10585 2.31306 2.66002 3.05902 3.51788 4.04556 7 8 9 10 = Present Value of 1 (Present Value of a Single Sum) 1 PVFni = (1 + )" (1+i)" (n) Periods 2% 2A%% 3% 4% 5% 6% 1 .98039 .97561 .97087 .96154 .95238 .94340 2 .96117 .95181 .94260 .92456 .90703 .89000 3 .94232 .92860 .91514 .88900 .86384 .83962 4 .92385 .90595 .88849 .85480 .82270 .79209 5 .90573 .88385 .86261 .82193 .78353 .74726 6 7 .88797 .87056 .85349 .86230 .84127 .82075 .83748 .81309 .78941 .79031 .75992 .73069 70950 .74622 .71068 .67684 .70496 .66506 .62741 O7 on 70 70040 CA1 50nn 8% (n) Periods .92593 .85734 .79383 .73503 .68058 Present Value of 1,(Present Value of a Single Sum) 9% 10% 11% 12% 15% .91743 .90909 .90090 .89286 .86957 .84168 .82645 .81162 .79719 .75614 .77218 .75132 .73119 .71178 .65752 .70843 .68301 .65873 .63552 .57175 .64993 .62092 .59345 .56743 49718 2 3 4 5 .63017 .58349 .54027 .50025 46319 .59627 .54703 .50187 .46043 .42241 .56447 .51316 .46651 42410 .38554 .53464 48166 43393 .39092 .35218 .50663 .45235 .40388 .36061 .32197 43233 .37594 32690 .28426 .24719 6 7 8 9 10 Future Value of an Ordinary Annuity of 1 (1+1)"-1 FVF-OA;= i 2% 212% 3% 4% 5% (n) Periods 6% 2 1.00000 2.02000 3.06040 4.12161 5.20404 1.00000 2.02500 3.07563 4.15252 5.25633 1.00000 2.03000 3.09090 4.18363 5.30914 1.00000 2.04000 3.12160 4.24646 5.41632 1.00000 2.05000 3.15250 4.31013 5.52563 1.00000 2.06000 3.18360 4.37462 5.63709 4 5 6 7 oc 6.30812 7.43428 8.58297 9.75463 10.94972 6.38774 7.54743 8.73612 9.95452 11.20338 6.46841 7.66246 8.89234 10.15911 11.46338 6.63298 7.89829 9.21423 10.58280 12.00611 6.80191 8.14201 9.54911 11.02656 12.57789 6.97532 8.39384 9.89747 11.49132 13.18079 10 8% 9% 15% (n) Periods 1.00000 2.08000 3.24640 4.50611 5.86660 1.00000 2.09000 3.27810 4.57313 5.98471 Future Value of an Ordinary Annuity of 1 10% 11% 12% 1.00000 1.00000 1.00000 2.10000 2.11000 2.12000 3.31000 3.34210 3.37440 4.64100 4.70973 4.77933 6.10510 6.22780 6.35285 1.00000 2.15000 3.47250 4.99338 6.74238 2 3 4 5 6 7.33592 8.92280 10.63663 12.48756 14.48656 7.52334 9.20044 11.02847 13.02104 15.19293 7.71561 9.48717 11.43589 13.57948 15.93743 7.91286 9.78327 11.85943 14.16397 16.72201 8.11519 10.08901 12.29969 14.77566 17.54874 8.75374 11.06680 13.72682 16.78584 20.30372 7 8 9 10 Present Value of an Ordinary Annuity of 1 1 1- (1+1) PVF-OAni = i (n) Periods 2% 2A%% 3% 4% 5% 6% 1 2 3 4 .98039 1.94156 2.88388 3.80773 4.71346 .97561 1.92742 2.85602 3.76197 4.64583 .97087 1.91347 2.82861 3.71710 4.57971 .96154 1.88609 2.77509 3.62990 4.45182 .95238 1.85941 2.72325 3.54595 4.32948 .94340 1.83339 2.67301 3.46511 4.21236 5 5.60143 6.47199 7.32548 8.16224 8.98259 5.50813 6.34939 7.17014 7.97087 8.75206 5.41719 6.23028 7.01969 7.78611 8.53020 5.24214 6.00205 6.73274 7.43533 8.11090 5.07569 5.78637 6.46321 7.10782 7.72173 4.91732 5.58238 6.20979 6.80169 7.36009 9 10 Present Value of an Ordinary Annuity of 1 10% 11% 12% 8% 9% 15% (n) Periods .92593 1.78326 2.57710 3.31213 3.99271 91743 1.75911 2.53130 3.23972 3.88965 .90909 1.73554 2.48685 3.16986 3.79079 90090 1.71252 2.44371 3.10245 3.69590 .89286 1.69005 2.40183 3.03735 3.60478 .86957 1.62571 2.28323 2.85498 3.35216 1 2 3 4 5 4.62288 5.20637 5.74664 6.24689 6.71008 4.48592 5.03295 5.53482 5.99525 6.41766 4.35526 4.86842 5.33493 5.75902 6.14457 4.23054 4.71220 5.14612 5.53705 5.88923 4.11141 4.56376 4.96764 5.32825 5.65022 3.78448 4.16042 4.48732 4.77158 5.01877 6 7 8 9 10 Present Value of an Annuity Due of 1 1 1- (1+0)7-1 Pn,i = 1+ i (n) Periods 2% 4% 5% 6% 1 2 3 4 5 1.00000 1.98039 2.94156 3.88388 4.80773 PVF-AD, 2A2% 3% 1.00000 1.00000 1.97561 1.97087 2.92742 2.91347 3.85602 3.82861 4.76197 4.71710 1.00000 1.96154 2.88609 3.77509 4.62990 1.00000 1.95238 2.85941 3.72325 4.54595 1.00000 1.94340 2.83339 3.67301 4.46511 7 8 9 10 5.71346 6.60143 7.47199 8.32548 9.16224 5.64583 6.50813 7.34939 8.17014 8.97087 5.57971 6.41719 7.23028 8.01969 8.78611 5.45182 6.24214 7.00205 7.73274 8.43533 5.32948 6.07569 6.78637 7.46321 8.10782 5.21236 5.91732 6.58238 7.20979 7.80169 Present Value of an Annuity Due of 1 10% 11% 8% 9% 12% 15% (n) Periods 1 1.00000 1.92593 2.78326 3.57710 4.31213 1.00000 1.91743 2.75911 3.53130 4.23972 1.00000 1.90909 2.73554 3.48685 4.16986 1.00000 1.90090 2.71252 3.44371 4.10245 1.00000 1.89286 2.69005 3.40183 4.03735 1.00000 1.86957 2.62571 3.28323 3.85498 2 3 4 5 6 4.99271 5.62288 6.20637 6.74664 7.24689 4.88965 5.48592 6.03295 6.53482 6.99525 4.79079 5.35526 5.86842 6.33493 6.75902 4.69590 5.23054 5.71220 6.14612 6.53705 4.60478 5.11141 5.56376 5.96764 6.32825 4.35216 4.78448 5.16042 5.48732 5.77158 7 8 9 10