Please complete in less than one hour. do not accept if you can not deliver.
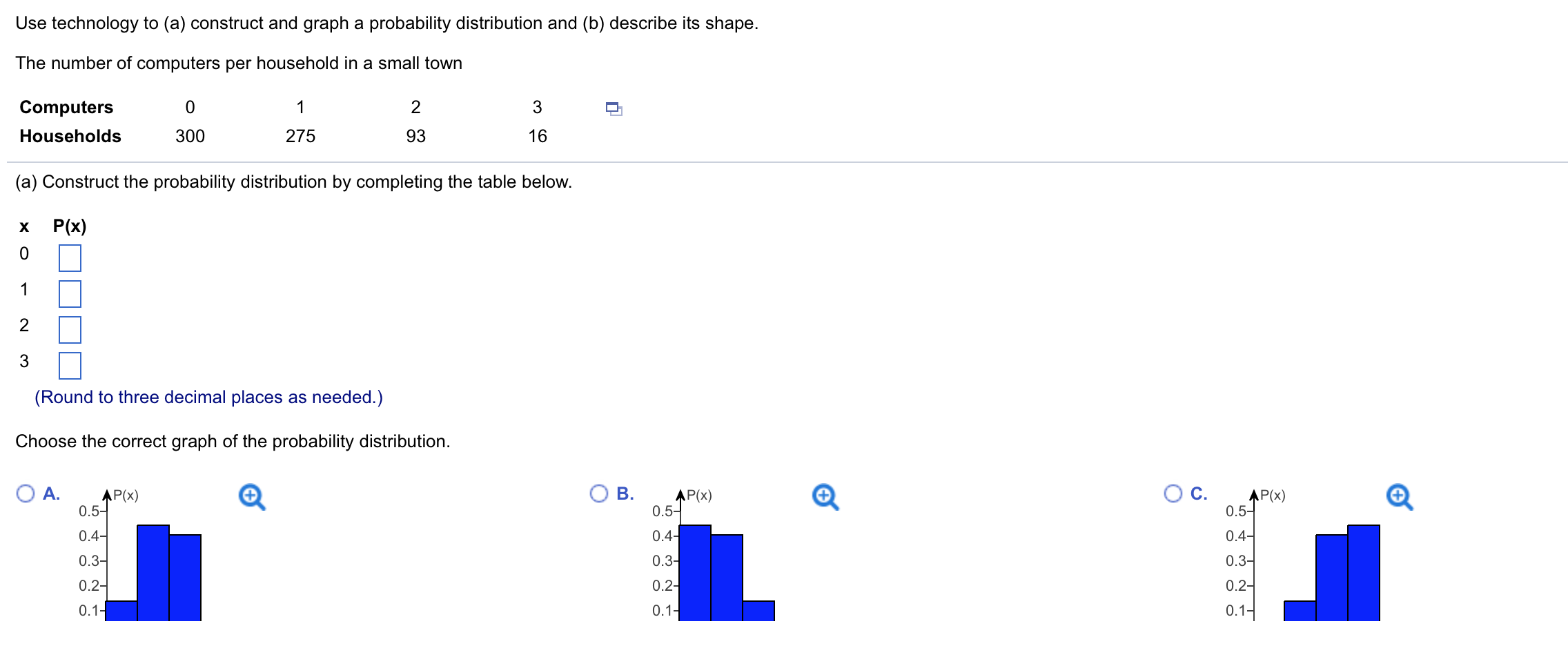
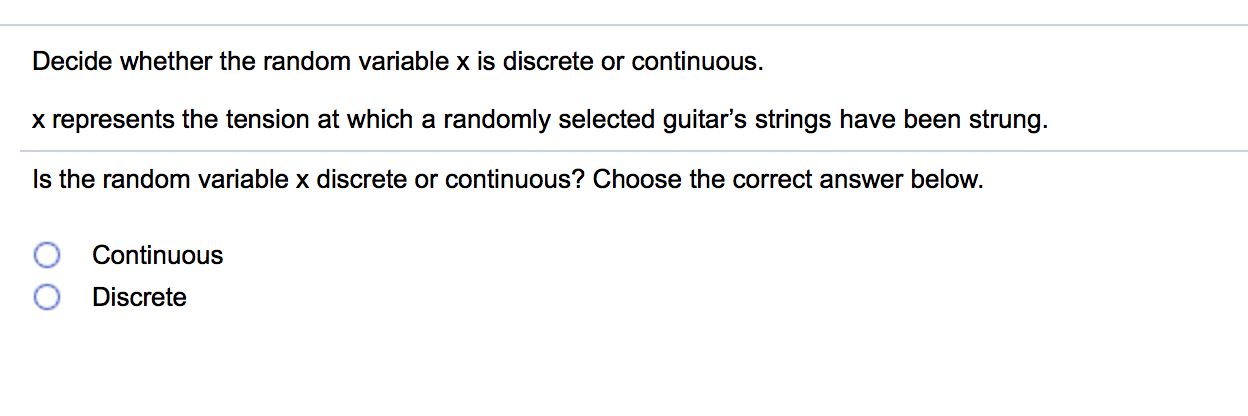
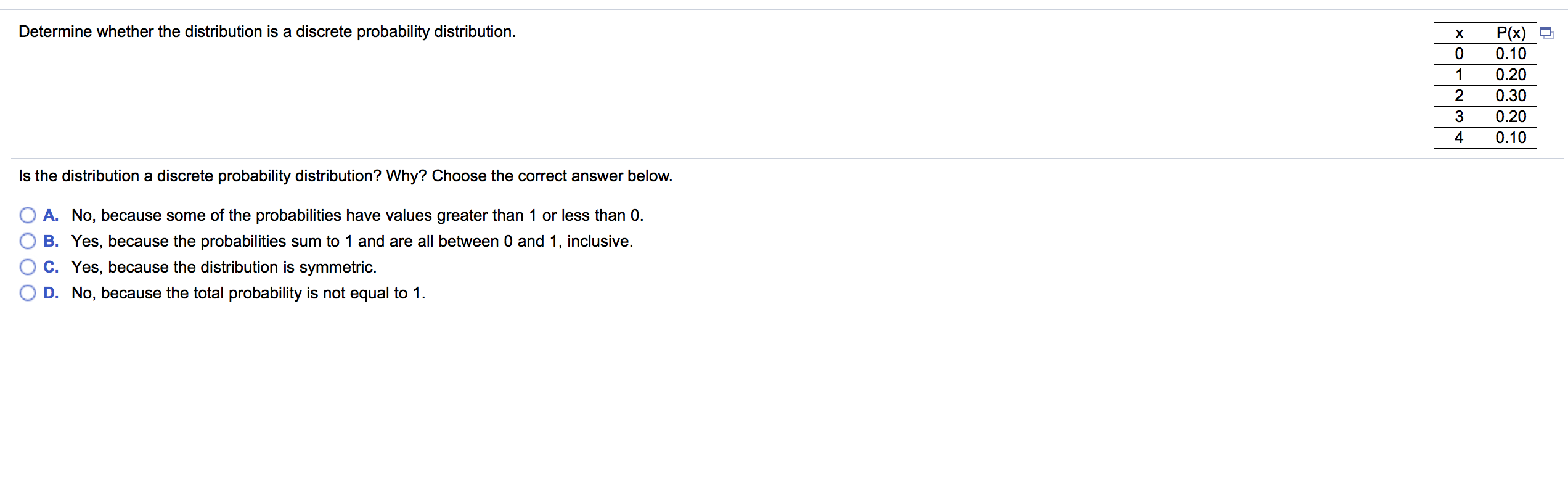
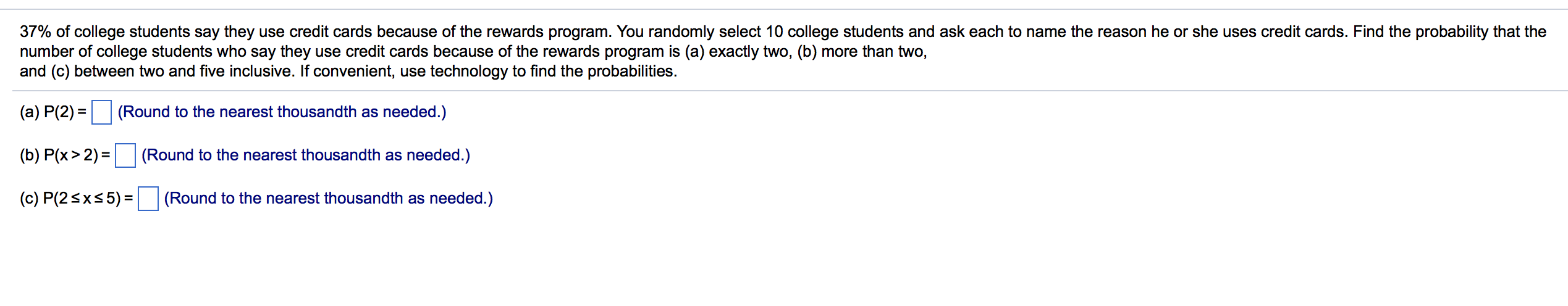
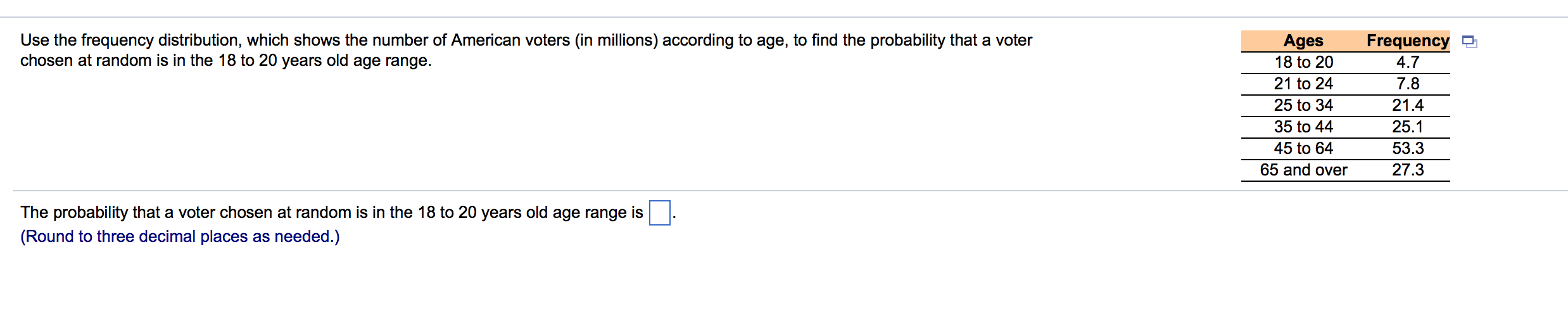
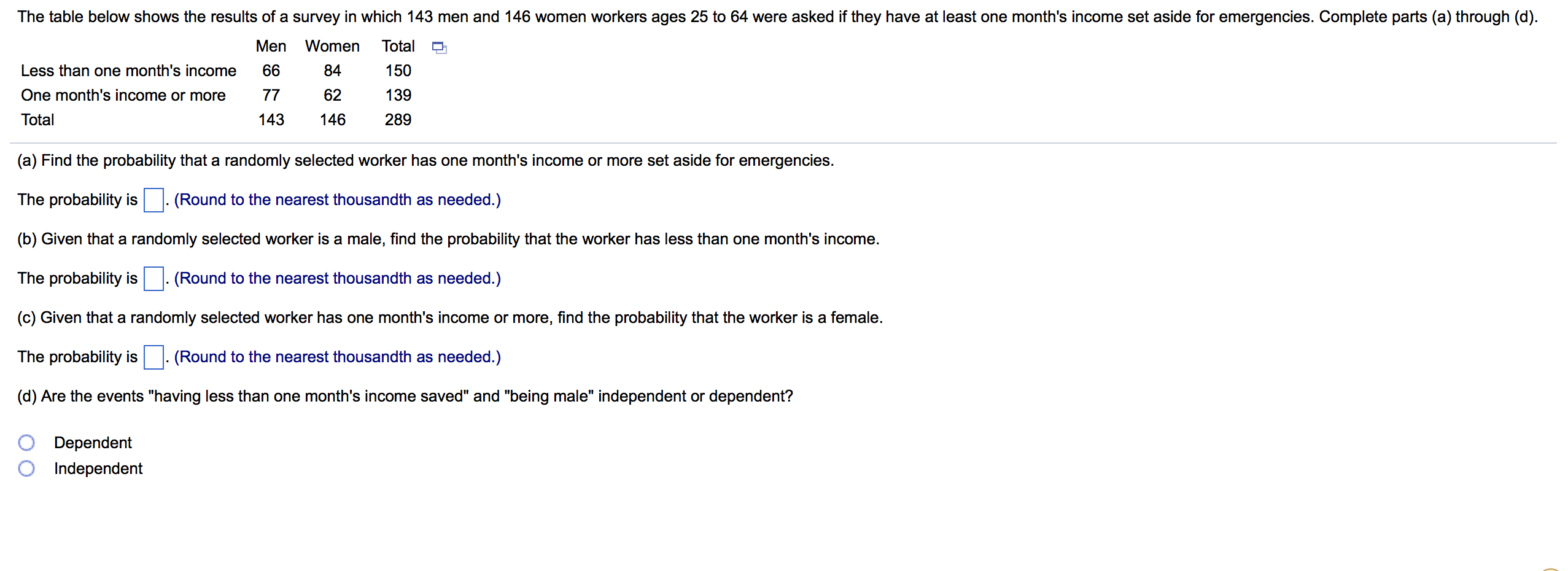
Evaluate the given expression and express the result using the usual format for writing numbers (instead of scientic notation). 4602 4602 = Cl O B. This is not a binomial experiment. Specify the value of q. Select the correct choice below and ll in any answer boxes in your choice. 0 B. This is not a binomial experiment. List the possible values of the random variable x. Find the mean, variance, and standard deviation of the binomial distribution with the given values of n and p. n = 90, p = 0.3 The mean, p, is El. (Round to the nearest tenth as needed.) The variance, 02, is D. (Round to the nearest tenth as needed.) The standard deviation, 0-, is D. (Round to the nearest tenth as needed.) (b) Describe the distribution's shape. Choose the correct answer below. 0 symmetric O skewed left 0 skewed right (e) Are the events "being female" and "being frequently involved in charity work" mutually exclusive? Explain. O A. No, because 203 females are frequently involved in charity work. 0 B. No, because no females are frequently involved in charity work. 0 6. Yes, because no females are frequently involved in charity work. 0 D. Yes, because 203 females are frequently involved in charity work. Use technology to (a) construct and graph a probability distribution and (b) describe its shape. The number of computers per household in a small town Computers Households (a) Construct the probability distribution by completing the table below. x P(x) 0 :l 1 2 3 :| (Round to three decimal places as needed.) Choose the correct graph of the probability distribution. CA. :I :l 0.4 0.3 0.2 0.1 P(x) 0 300 (+1 1 275 2 93 3 16 OB. 0.4 0.3 0.2 01 F300 00. 0.4 0.3 0.2 0.1 P(x) Decide whether the random variable x is discrete or continuous. x represents the tension at which a randomly selected guitar's strings have been strung. Is the random variable x discrete or continuous? Choose the correct answer below. 0 Continuous 0 Discrete The table below shows the results of a survey that asked 2871 people whether they are involved in any type of charity work. A person is selected at random from the sample. Complete parts (a) through (e). Frequently Occasionally Not at all Total g Male 221 453 796 1470 Female 203 450 748 1401 Total 424 903 1544 2871 (a) Find the probability that the person is frequently or occasionally involved in charity work. P(being frequently involved or being occasionally involved) = (Round to the nearest thousandth as needed.) (b) Find the probability that the person is female or not involved in charity work at all. P(being female or not being involved) = (Round to the nearest thousandth as needed.) (c) Find the probability that the person is male or frequently involved in charity work. P(being male or being frequently involved)= (Round to the nearest thousandth as needed.) (d) Find the probability that the person is female or not frequently involved in charity work. P(being female or not being frequently involved) = (Round to the nearest thousandth as needed.) Find the indicated probabilities using the geometric distribution. the Poisson distribution. or the binomial distribution. Then determine if the events are unusual. If convenient, use the appropriate probability table or technology to nd the probabilities. A newspaper nds that the mean number of typographical errors per page is ve. Find the probability that (a) exactly four typographical errors are found on a page, (b) at most four typographical errors are found on a page, and (c) more than four typographical errors are found on a page. (a) P(exactly four typographical errors are found on a page) = (Round to four decimal places as needed.) (b) P(at most four typographical errors are found on a page)= (Round to four decimal places as needed.) (c) P(more than four typographical errors are found on a page) = (Round to four decimal places as needed.) Which of the events are unusual? Select all that apply. :I A. The event in part (a) is unusual. :I B. The event in part (b) is unusual. :l c. The event in part (c) is unusual. :I D. None of the events are unusual. A doctor gives a patient a 90% chance of surv'wing bypass surgery after a heart attack. If the patient survives the surgery. then the patient has a 25% chance that the heart damage will heal. Find the probability that the patient survives the surgery and the heart damage heals. The probability is . (Type an integer or a decimal.) \fP(x) '21 0.10 0.20 0.30 0.20 0.10 Determine whether the distribution is a discrete probability distribution. #MNAOX Is the distribution a discrete probability distribution? Why? Choose the correct answer below. 0 A. No, because some of the probabilities have values greater than 1 or less than 0. O B. Yes, because the probabilities sum to 1 and are all between 0 and 1, inclusive. O C. Yes, because the distribution is symmetric. O D. No, because the total probability is not equal to 1. Complete parts (a) and (b) using the probability distribution below. The number of overtime hours worked in one week per employee Overtime hours 0 'l 2 3 Probability 0.034 0.092 0.165 0.282 (a) Find the mean, variance, and standard deviation of the probability distribution. Find the mean of the probability distribution. p = (Round to one decimal place as needed.) Find the variance of the probability distribution. 02 = (Round to one decimal place as needed.) Find the standard deviation of the probability distribution. o = (Round to one decimal place as needed.) (b) Interpret the results in the context of the real-life situation. 0 A. An employee works an average of 2.2 overtime hours per week with a standard deviation of approximately 1.5 hours. 0 B. An employee works an average of 3.3 overtime hours per week with a standard deviation of approximately 1.5 hours. 0 C. An employee works an average of 1.5 overtime hours per week with a standard deviation of approximately 3.3 hours. 0 D. An employee works an average 3.3 of overtime hours per week with a standard deviation of approximately 7 hours. 0.199 0.160 0.068 Suppose Jim is going to burn a compact disk (CD) that will contain 5 songs. In how many ways can Jim arrange the 5 songs on the CD? Jim can burn the 5 songs on the CD in D different ways. For the given pair of events, classify the two events as independent or dependent. Studying regularly Getting a good grade Choose the correct answer below. 0 A. The two events are independent because the occurrence of one affects the probability of the occurrence of the other. 0 B. The two events are dependent because the occurrence of one does not aect the probability of the occurrence of the other. 0 C. The two events are independent because the occurrence of one does not affect the probability of the occurrence of the other. 0 D. The two events are dependent because the occurrence of one affects the probability of the occurrence of the other. Acompany that makes canons nds that the probability of producing a carton with a puncture is 0.06, the probability that a carton has a smashed oomer is 0.1, and the probability that a carton has a puncture and has a smashed comer is 0.006. Answer parts (a) and (b) below. (a) Are the events "selecting a carton with a puncture" and "selecting a carton with a smashed comer' mutually exclusive? Explain. O A. Yes, a carton can have a puncture and a smashed corner. O B. Yes, a carton cannot have a puncture and a smashed corner. 0 c. No, a carton cannot have a puncture and a smashed corner. 0 D. No, a carton can have a puncture and a smashed corner. (b) If a quality inspector randomly selects a carton, nd the probability that the carton has a puncture or has a smashed corner. The probability that a carton has a puncture or a smashed corner is (Type an integer or a decimal. Do not round.) 37% of college students say they use credit cards because of the rewards program. You randomly select 10 college students and ask each to name the reason he or she uses credit cards. Find the probability that the number of college students who say they use credit cards because of the rewards program is (a) exactly two, (b) more than two. and (c) between two and ve inclusive. If convenient, use technology to nd the probabilities. (a) P(2) = (Round to the nearest thousandth as needed.) (b) P(x > 2) = (Round to the nearest thousandth as needed.) (c) P(2 S x S 5) = (Round to the nearest thousandth as needed.) Use the frequency distribution, which shows the number of American voters (in millions) according to age, to nd the probability that a voter Ages Frequency l3 chosen at random is in the 18 to 20 years old age range. 18 to 20 4.7 21 to 24 7.8 25 to 34 21.4 35 to 44 25.1 45 to 64 53.3 M The probability that a voter chosen at random is in the 18 to 20 years old age range is (Round to three decimal places as needed.) About 60% of babies born with a certain ailment recover fully. A hospital is caring for ve babies born with this ailment. The random variable represents the number of babies that recover fully. Decide whether the experiment is a binomial experiment. If it is, identify a success, specify the values of n, p, and q, and list the possible values of the random variable x. Is the experiment a binomial experiment? 0 No 0 Yes What is a success in this experiment? O This is not a binomial experiment. 0 Babydoesn't recover 0 Baby recovers Specify the value of n. Select the correct choice below and ll in any answer boxes in your choice. OA. n: O B. This is not a binomial experiment. Specify the value of p. Select the correct choice below and ll in any answer boxes in your choice. OA. 9: O B. This is not a binomial experiment. Specify the value of a. Select the correct choice below and ll in anv answer boxes in vour choice. The table below shows the results of a survey in which 143 men and 146 women workers ages 25 to 64 were asked if they have at least one month's income set aside for emergencies. Complete parts (a) through (d). Men Women Total % Less than one month's income 66 84 150 One month's income or more 77 62 139 Total 1 43 1 46 289 (a) Find the probability that a randomly selected worker has one month's income or more set aside for emergencies. The probability is . (Round to the nearest thousandth as needed.) (b) Given that a randomly selected worker is a male. nd the probability that the worker has less than one month's income. The probability is . (Round to the nearest thousandth as needed.) (0) Given that a randomly selected worker has one month's income or more, nd the probability that the worker is a female. The probability is . (Round to the nearest thousandth as needed.) (d) Are the events "having less than one month's income saved" and "being male" independent or dependent? O Dependent 0 Independent A probability experiment consists of rolling a fair 15-sided die. Find the probability of the event below. rolling a number divisible by 5 The probability is E. (Type an integer or decimal rounded to three decimal places as needed.)
