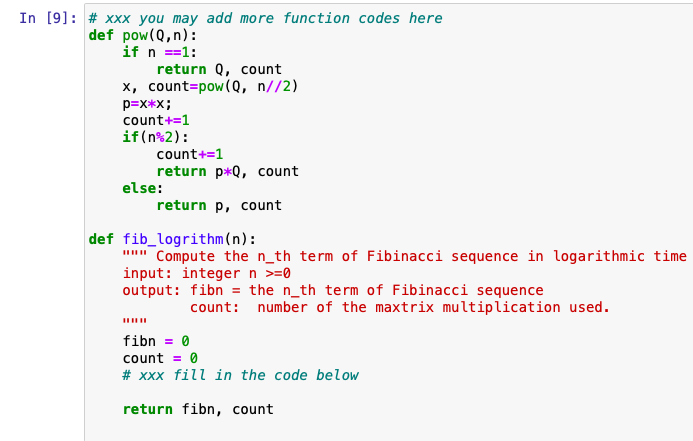
Please complete the code using above requirement

Approach B: Recursive Matrix Approach in Logarithmic Time See details at https://mathworld.wolfram.com/FibonacciQ-Matrix.html First, define Q = [F(2) F(1)| = IF(1) F(0)1 | 111 | 101 = 101 Qan Q^(n-1) * 0 Q^n |F(n+1) F(n) | IF(n) F(n-1) 1 | 111 IF(n) F(n-1) IF(n-1) F(n-2) 1 Then, we can compute (^n in T(n)=0(log n) time with the pseudocode below. Note that * F(n) is actully equal to (0^n) [0] [1] * the code does not work when n==0 * your code should also count the number of operations (matrx multiplications) used # T(n): total number of matrix multiplications used def pow (Q, n): if n=-1: return Q x = pow (Q, n/2) p = X* X; if (n % 2) return p*Q; else return pi # T(n/2) matrix multiplications used # 1 more matrix multiplication used # 1 more matrix multiplication used In [9]: # xxx you may add more function codes here def pow(Q,n): if n ==1: return 0, count X, count=pow(Q, n//2) p=X*X; count+=1 if(n%2): count+=1 return p*Q, count else: return p, count def fib_logrithm(n): " Compute the n_th term of Fibinacci sequence in logarithmic time input: integer n >=0 output: fibn = the n_th term of Fibinacci sequence count: number of the maxtrix multiplication used. fibn = 0 count = 0 # xxx fill in the code below return fibn, count Approach B: Recursive Matrix Approach in Logarithmic Time See details at https://mathworld.wolfram.com/FibonacciQ-Matrix.html First, define Q = [F(2) F(1)| = IF(1) F(0)1 | 111 | 101 = 101 Qan Q^(n-1) * 0 Q^n |F(n+1) F(n) | IF(n) F(n-1) 1 | 111 IF(n) F(n-1) IF(n-1) F(n-2) 1 Then, we can compute (^n in T(n)=0(log n) time with the pseudocode below. Note that * F(n) is actully equal to (0^n) [0] [1] * the code does not work when n==0 * your code should also count the number of operations (matrx multiplications) used # T(n): total number of matrix multiplications used def pow (Q, n): if n=-1: return Q x = pow (Q, n/2) p = X* X; if (n % 2) return p*Q; else return pi # T(n/2) matrix multiplications used # 1 more matrix multiplication used # 1 more matrix multiplication used In [9]: # xxx you may add more function codes here def pow(Q,n): if n ==1: return 0, count X, count=pow(Q, n//2) p=X*X; count+=1 if(n%2): count+=1 return p*Q, count else: return p, count def fib_logrithm(n): " Compute the n_th term of Fibinacci sequence in logarithmic time input: integer n >=0 output: fibn = the n_th term of Fibinacci sequence count: number of the maxtrix multiplication used. fibn = 0 count = 0 # xxx fill in the code below return fibn, count