Please complete the projectile_motion_drag codes: (It is same as the above question but more clear)

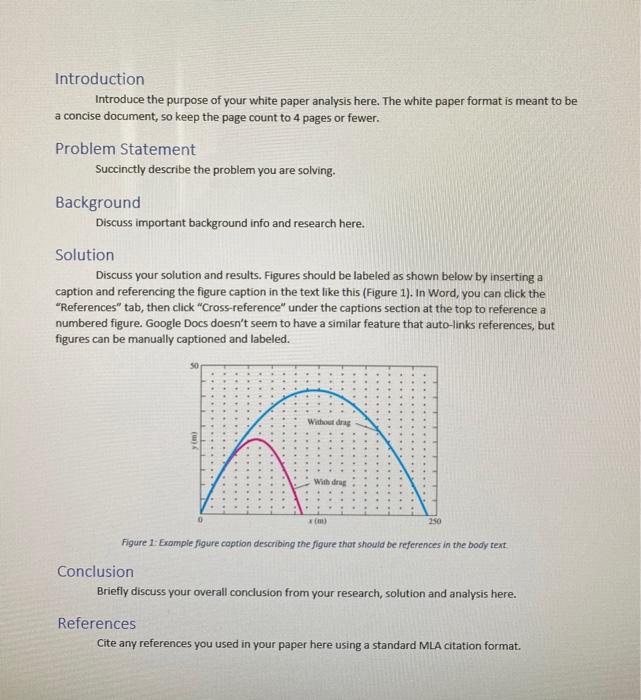
And then if it is possible fill Intro-conclusion of that process:

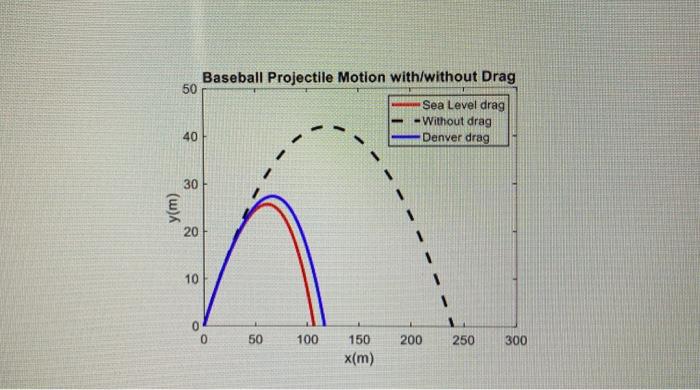
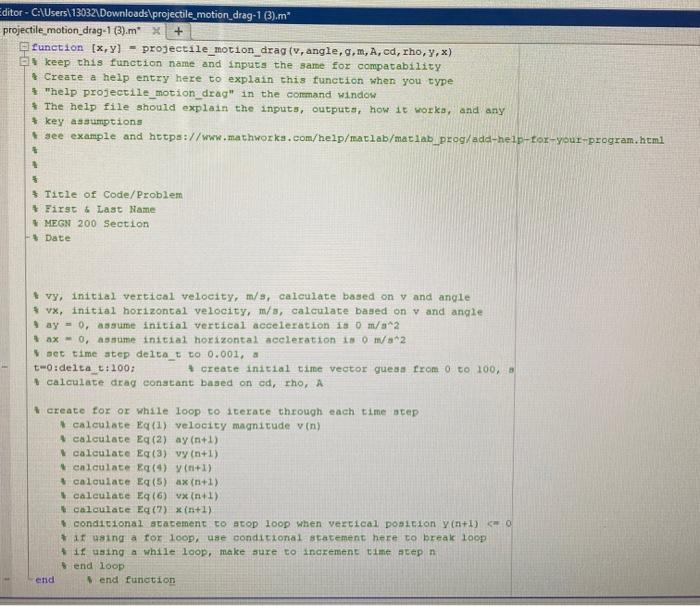
SO Without drag m) With drag im) Part 1: Baseball Projectile Model with Aerodynamic Drag The Rock's jump can be modeled with reasonable accuracy using projectile motion equations from physics, but we should add in the effect of air resistance to the projectile motion model to account for the drag force acting against The Rock during the jump because he presents a large area and would have to be moving pretty fast. This reference from a Dynamics textbook will be helpful to develop the Matlab model of projectile motion with drag We'll start with the algorithm and values from this Dynamics textbook reference and replicate their results for a baseball as a starting point to validate the model of projectile motion with air resistance. The algorithm uses the same basic projectile motion model from physics, but modifies the acceleration terms to account for the effects of the aerodynamic drag force. You will need to write a standalone Matlab function called "projectile_motion_drag" that computes 2D projectile motion trajectories for given parameters passed into the function. This function should take as inputs the initial conditions and mass and drag properties of the modeled problem. Outputs should be provided as a result of "projectile_motion_drag" and they should at least include the x and y coordinates of the trajectory over time. The equations for the algorithm and commented pseudocode are listed below: % create projectile_motion_drag function in projectile_motion_drag.m file % inputs should be: v(velocity magnitude), angle (jump angle), g (gravity), m (projectile mass) % A (projected area), cd (drag coefficient), rho (air density) %y (initial vertical position), x (initial horizontal position) % outputs should be: x (horizontal position vector), y (vertical position vector) function (x,y] =projectile_motion_drag(v angle,g,m, A,cd, rho.y.x) % establish initial values for a_x,v_x, x, a_y, v_y, y based on function inputs (assume a_x= a_y=0) % calculate drag constant D based on function inputs rho, cd, and A D=(rho * cd * A) 1 1 % establish an initial guess for the time t to start simulation, where end_t is around 100 seconds and At is a sufficiently small time step to effectively capture data (0.01 or 0.001 s) t=0: At :end_t; % create a for or while loop to loop through time step values % implement the following projectile motion equations in code for each timestep n: v(n) = Jv;(n) + v (n) Eg(1) Qy(n+1) = -g--v(n) vy(n) Eg(2) wy(n + 1) = v(n) + ay(n). At Eq(3) y (n + 1) = y(n) + v,(n). At+ay (n). At? Eg(4) ax(n + 1) =-.v(n). v, (n) Eq(5) Vy (n + 1) = 0, (n) + ax (n). At Eq(6) * (n + 1) = x(n) + v, (n). At + ax (n). At^2 Eq(7) % if using a for loop, make sure to include a conditional if statement to break out of the loop (i.e. use a break statement if y(n+1)