Answered step by step
Verified Expert Solution
Question
1 Approved Answer
( ( ( Please Dont copy other answers and i need this code de to produced the output provided in the pic ) ) )
Please Dont copy other answers and i need this code de to produced the output provided in the picActivity #: More linear interpolation individual
In the team lab, your team put together a program that interpolated between two position values based on the time values when each positon was observed. This was a onedimensional D interpolation, since you were interpolating only a single value, the distance traveled by the ISS. You are now going to extend that program to one that will linearly interpolate between two points in D
Let's say we are tracking the change of a satellite's position with time. So at time to the position is and at time the position is What is the position at some time between to and
Refer again to the Linear Interpolation material associated with the team lab. That material describes the development of the equation representing linear interpolation of a dependent variable versus an independent variable For the current problem, what varies linearly with what? What are the dependent variables What are the independent variables
Let's assume that each of the position variables varies linearly with time Therefore, time is the independent variable in each case. This means we can perform linear interpolation three separate times to get what we need. This can be done in three steps: linearly interpolate between and for with as the result; repeat for and for with as the result; repeat for and for with as the result. The result will be associated with time
a Write a program named morelinearinterpolation.py that will take two observed D positions at two points in time, and then will calculate the D position at a third point in time. Let's consider only times between the two observed times. You should output the and values for that position on separate lines. Begin by identifying the variables you will use, the names for those variables, and the computations that should occur for those variables. Then, write a program that will output the D position of the interpolated point on separate lines.
For this initial program, use the following data values:
At time seconds, observed position was meters
At time seconds, observed position was meters
You want to find the position at time seconds
Example output:
At time seconds:
b Now, add to your file morelinearinterpolation.py from above. Modify your program in the following ways:
i When printing the position, follow the output by a line of dashes
ii Instead of just computing the interpolation at one point and printing the result, you will now compute it at points. You may copy and paste the portion of your code that is needed to recompute interpolation times.
iii. Create variables for the starting time of interpolation, and the ending time of interpolation. Display the results from interpolating at points, evenly spaced from the beginning time to the ending time, inclusive.
iv Interpolate, starting at time seconds and ending at time seconds, printing the result each time. The line of dashes will separate each computation. Note: later we will see how we can do this more efficiently, without copyingandpasting code, but for now, copyandpaste your code.
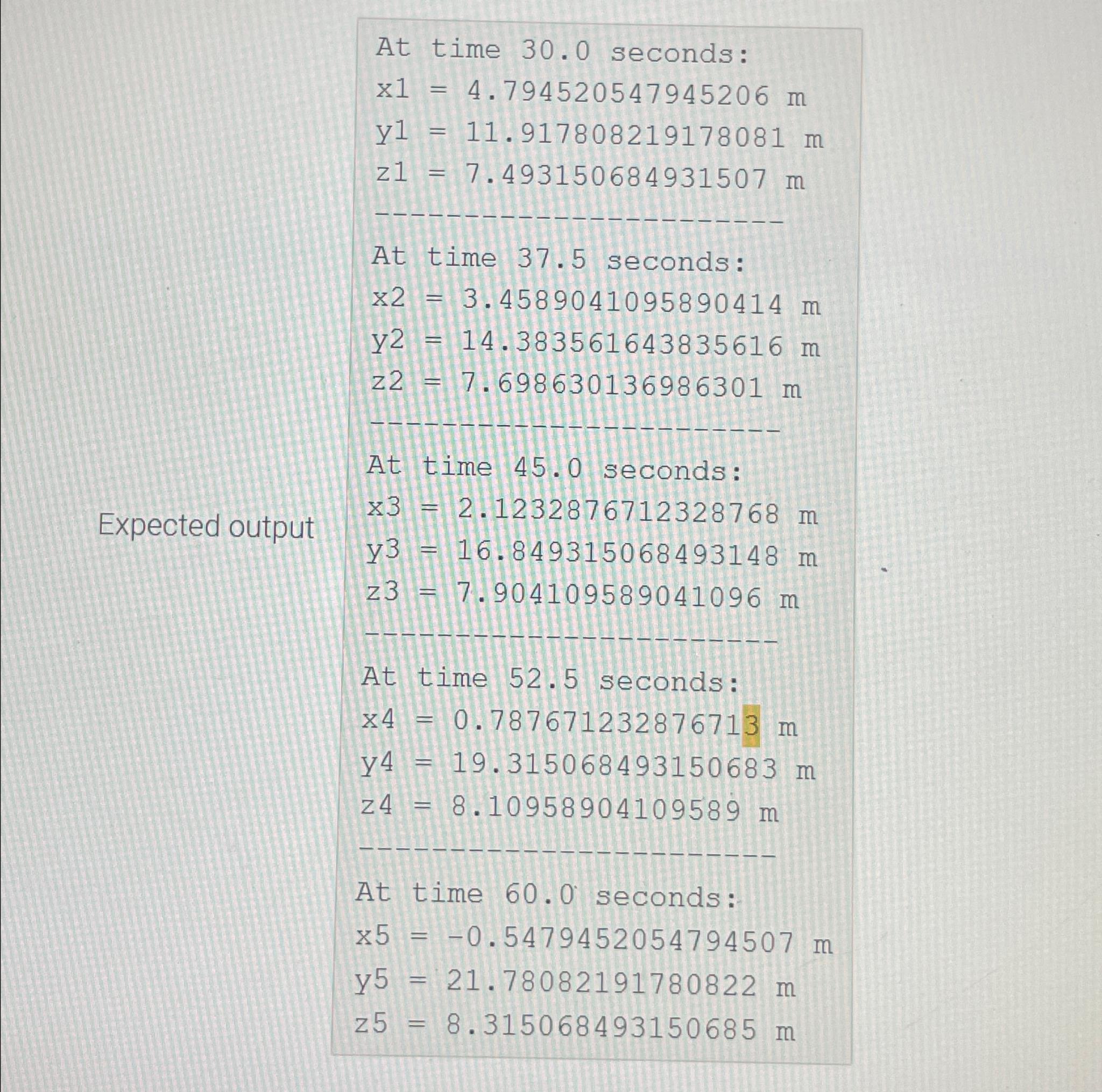
At time seconds:
At time seconds:
Expected output
At time seconds:
At time seconds:
At time seconds:
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


