PLEASE DONT JUST GIVE SKELETON CODE

THIS IS WHAT I KNOW SO FAR

Please don't post skeleton code I need more help than that

So far I have this knowledge

LL Parser Generator

In syntax analysis we learned how LL(1) PREDICT sets are constructed from FIRST and FOLLOW sets. In the current project you will build, in a purely functional subset of Scheme, a parser generator that implements these constructions.

To get you started, Im providing a 300-line skeleton file. You will want to study the code in this file carefully.

The key function you are to implement is the following:

(define parse-table

(lambda (grammar)

your code here; my version is about 15 lines long,

(but it calls other functions described below)

))

The input grammar must consist of a list of lists, one per non-terminal in the grammar. The first elementof each sub-list should be the non-terminal; the remaining elements should be the right-hand sides of the productions for which that non-terminal is the left-hand side. The sub-list for the start symbol must come first. Every grammar symbol must be represented as a quoted string. As an example, here is our familiar LL(1) calculator grammar in the required format:

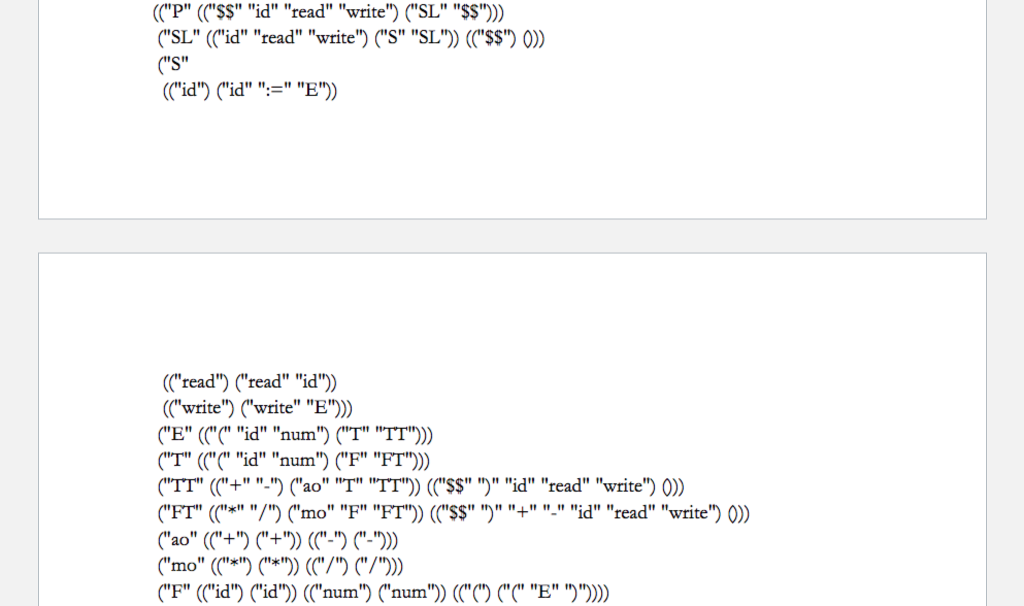
(define calc-gram

'(("P" ("SL" "$$"))

("SL" ("S" "SL") ())

("S" ("id" ":=" "E") ("read" "id") ("write" "E"))

("E" ("T" "TT"))

("T" ("F" "FT"))

("TT" ("ao" "T" "TT") ())

("FT" ("mo" "F" "FT") ())

("ao" ("+") ("-"))

("mo" ("*") ("/"))

("F" ("id") ("num") ("(" "E" ")"))

))

The parse table, as returned by function parse-table, must have the same format, except that every right-hand side is replaced by a pair (a 2-element list) whose first element is the predict set for the corresponding production, and whose second element is the right-hand side. If you type

(parse-table calc-gram)

the Scheme interpreter should respond

(("P" (("$$" "id" "read" "write") ("SL" "$$")))

("SL" (("id" "read" "write") ("S" "SL")) (("$$") ()))

("S"

(("id") ("id" ":=" "E"))

(("read") ("read" "id"))

(("write") ("write" "E")))

("E" (("(" "id" "num") ("T" "TT")))

("T" (("(" "id" "num") ("F" "FT")))

("TT" (("+" "-") ("ao" "T" "TT")) (("$$" ")" "id" "read" "write") ()))

("FT" (("*" "/") ("mo" "F" "FT")) (("$$" ")" "+" "-" "id" "read" "write") ()))

("ao" (("+") ("+")) (("-") ("-")))

("mo" (("*") ("*")) (("/") ("/")))

("F" (("id") ("id")) (("num") ("num")) (("(") ("(" "E" ")"))))

A parse function is provided that accepts a grammar and an input string as arguments. It calls the parse-table function and then uses it to parse the input, printing a trace of its actions as it does so, in a manner reminiscent of the Dparse output from the PL/0 compiler. You can use this function to test your code.

A possible implementation strategy

There are many ways to implement parse-table. Feel free to choose whatever strategy appeals to you. If youre not sure where to start, there is a skeleton of a few routines that may provide some guidance. These dont necessarily embody the best strategy.

This code uses two main data structures: a right context structure and a knowledge structure. A right-context function is provided to generate the former for any given

symbol B. The function returns a list of pairs. Each pair consists of a symbol A and a list of symbols such that for some , A B . As an example, if you type

(right-context "SL" calc-gram)

the Scheme interpreter should respond

(("P" ("$$")) ("SL" ()))

This tells us that SL appears on the right-hand of two productions in the grammar: one with P on the left-hand side and one with SL on the left-hand side. In the former, the portion of the right-hand side after the SL is $$. In the latter, the portion of the right-hand side after the SL is empty (that is, SL is the last thing on the right-hand side). In a similar vein, if you type

(right-context "mo" calc-gram)

the Scheme interpreter should respond

(("FT" ("F" "FT")))

This tells us there is only one production with a mo on the right-hand side. It has FT on the left-hand side, and F FT after the mo on the right-hand side.

The right-context information is useful for constructing FOLLOW sets.

Assuming you use the suggested strategy, you will need to compute the knowledge structure recursively. This structure consists of a list of 4-element sub-lists, one per non-terminal. Each

sub-list contains (1) the non -terminal itself (call it A), (2) a Boolean indicating whether we currently think that A * , (3) our current estimate of FIRST(A) {}, and (4) our current estimate of FOLLOW(A) {}. It is much easier in to keep track of separately, rather than to

include it in the FIRST and FOLLOW sets.

The function to generate the knowledge structure is

(define get-knowledge

(lambda (grammar)

;;; your code here; my version is a little under 30 lines

))

If you type

(get-knowledge calc-gram)

the interpreter should respond

(("P" #f ("$$" "id" "read" "write") ())

("SL" #t ("id" "read" "write") ("$$"))

("S" #f ("id" "read" "write") ("$$" "id" "read" "write"))

("E" #f ("(" "id" "num") ("$$" ")" "id" "read" "write"))

("T" #f ("(" "id" "num") ("$$" ")" "+" "-" "id" "read" "write"))

("TT" #t ("+" "-") ("$$" ")" "id" "read" "write"))

("FT" #t ("*" "/") ("$$" ")" "+" "-" "id" "read" "write"))

("ao" #f ("+" "-") ("(" "id" "num"))

("mo" #f ("*" "/") ("(" "id" "num"))

("F" #f ("(" "id" "num") ("$$" ")" "*" "+" "-" "/" "id" "read" "write")))

This tells us, for example, that FT generates epsilon, but F does not, and that FOLLOW(mo) = {(, id, num}.

As the base of its recursion, get-knowledge uses an initial, empty structure generated by function initial-knowledge, which is provided. At each step of the recursion the function makes use of utility routines that extract information from the current structure:

(define generates-epsilon?

(lambda (w knowledge grammar)

;;; your code here; my version is 7 lines long

))

(define first

(lambda (w knowledge grammar)

;;; your code here; my version is 10 lines long

))

(define follow

(lambda (A knowledge)

(cadddr (symbol-knowledge A knowledge))))

This is simpler than the other two functions, because it only needs

to work for individual non-terminals, not for lists of symbols.

If you work in pairs on this assignment, one possible division of labor is for one partner to

write generates-epsilon?, first, and parse-table, while the other partner writes get-

knowledge. A better strategy, however, may be to start by having one partner write generates-

epsilon? while the other writes first.

We have learned how LL(1) PREDICT sets are constructed from FIRST and FOLLOW sets. In the second part of Project 2, you will build a parser generator that implements these constructions in a purely functional subset of Scheme. The key function you are to implement is the following (lambda (grammar) " your code here; The input grammar must consist of a list of lists, one per non-terminal in the grammar. The first element of each sublist should be the non-terminal; the remaining elements should be the right- hand sides of the productions for which that non-terminal is the left-hand side. The sublist for the start symbol must come first. Every grammar symbol must be represented as a quoted string. As an example, here is our familiar LL(1) calculator grammar in the required format: We have learned how LL(1) PREDICT sets are constructed from FIRST and FOLLOW sets. In the second part of Project 2, you will build a parser generator that implements these constructions in a purely functional subset of Scheme. The key function you are to implement is the following (lambda (grammar) " your code here; The input grammar must consist of a list of lists, one per non-terminal in the grammar. The first element of each sublist should be the non-terminal; the remaining elements should be the right- hand sides of the productions for which that non-terminal is the left-hand side. The sublist for the start symbol must come first. Every grammar symbol must be represented as a quoted string. As an example, here is our familiar LL(1) calculator grammar in the required format