please elaborate on your comment.
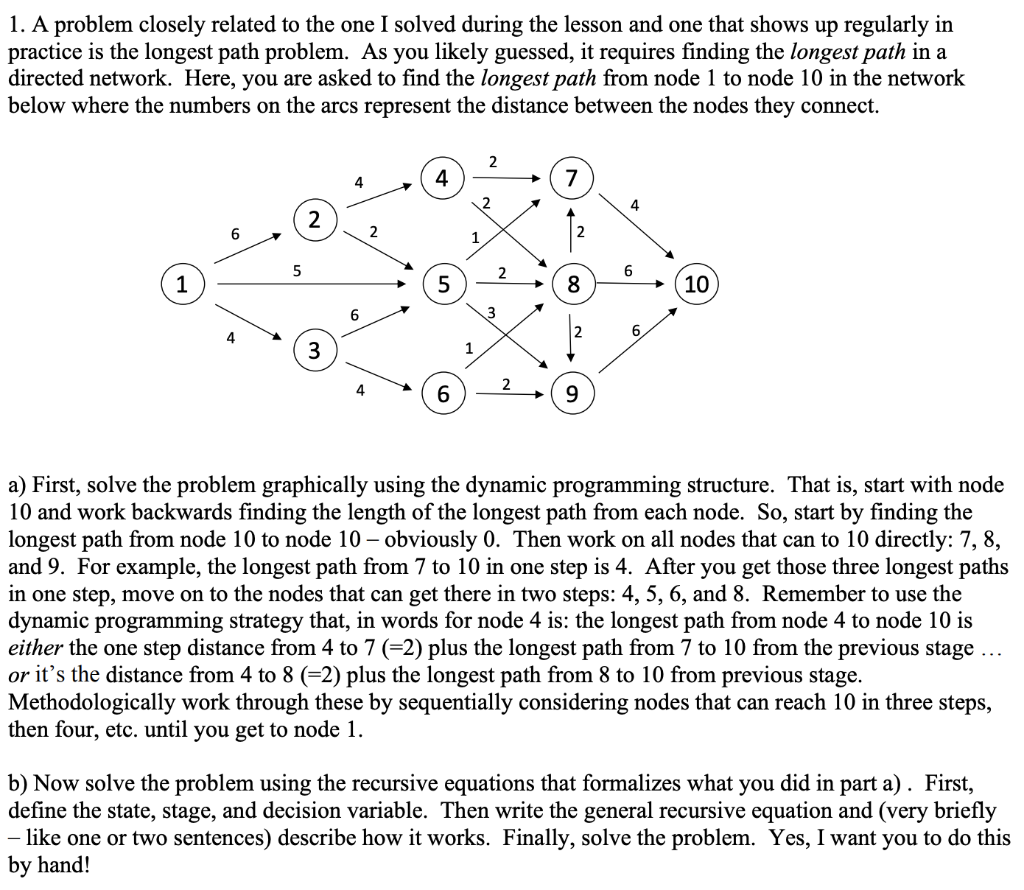
1. A problem closely related to the one I solved during the lesson and one that shows up regularly in practice is the longest path problem. As you likely guessed, it requires finding the longest path in a directed network. Here, you are asked to find the longest path from node 1 to node 10 in the network below where the numbers on the arcs represent the distance between the nodes they connect. 4 4 2 4 2 6 2 2 5 6 1 5 8 10 6 3 2 3 6 9 a) First, solve the problem graphically using the dynamic programming structure. That is, start with node 10 and work backwards finding the length of the longest path from each node. So, start by finding the longest path from node 10 to node 10 - obviously 0. Then work on all nodes that can to 10 directly: 7, 8, and 9. For example, the longest path from 7 to 10 in one step is 4. After you get those three longest paths in one step, move on to the nodes that can get there in two steps: 4, 5, 6, and 8. Remember to use the dynamic programming strategy that, in words for node 4 is: the longest path from node 4 to node 10 is either the one step distance from 4 to 7 (=2) plus the longest path from 7 to 10 from the previous stage ... or it's the distance from 4 to 8 (32) plus the longest path from 8 to 10 from previous stage. Methodologically work through these by sequentially considering nodes that can reach 10 in three steps, then four, etc. until you get to node 1. b) Now solve the problem using the recursive equations that formalizes what you did in part a). First, define the state, stage, and decision variable. Then write the general recursive equation and (very briefly like one or two sentences) describe how it works. Finally, solve the problem. Yes, I want you to do this by hand! 1. A problem closely related to the one I solved during the lesson and one that shows up regularly in practice is the longest path problem. As you likely guessed, it requires finding the longest path in a directed network. Here, you are asked to find the longest path from node 1 to node 10 in the network below where the numbers on the arcs represent the distance between the nodes they connect. 4 4 2 4 2 6 2 2 5 6 1 5 8 10 6 3 2 3 6 9 a) First, solve the problem graphically using the dynamic programming structure. That is, start with node 10 and work backwards finding the length of the longest path from each node. So, start by finding the longest path from node 10 to node 10 - obviously 0. Then work on all nodes that can to 10 directly: 7, 8, and 9. For example, the longest path from 7 to 10 in one step is 4. After you get those three longest paths in one step, move on to the nodes that can get there in two steps: 4, 5, 6, and 8. Remember to use the dynamic programming strategy that, in words for node 4 is: the longest path from node 4 to node 10 is either the one step distance from 4 to 7 (=2) plus the longest path from 7 to 10 from the previous stage ... or it's the distance from 4 to 8 (32) plus the longest path from 8 to 10 from previous stage. Methodologically work through these by sequentially considering nodes that can reach 10 in three steps, then four, etc. until you get to node 1. b) Now solve the problem using the recursive equations that formalizes what you did in part a). First, define the state, stage, and decision variable. Then write the general recursive equation and (very briefly like one or two sentences) describe how it works. Finally, solve the problem. Yes, I want you to do this by hand
