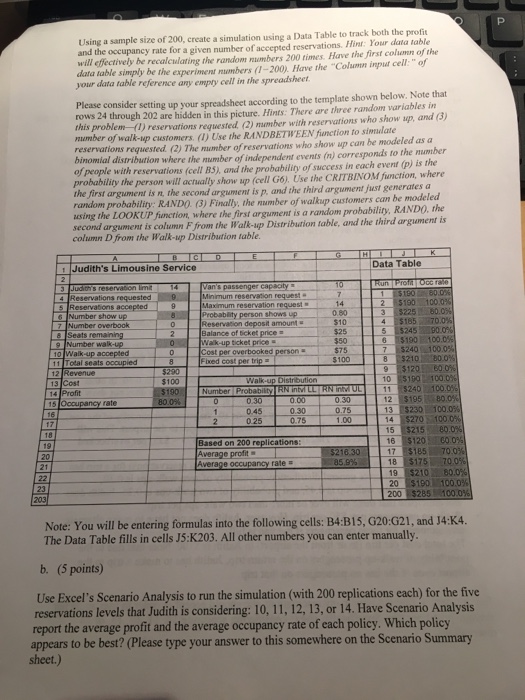
Please e-mail your completed files to lan.luo@wsu.edu. This assignment may be completed in a group of up to four people. Please state in the email message the names of all persons turning in this assignment. Please put "MgtOp 470 Homework 6" followed by the name of the person who sent the email in the Subject of the email. I. a. (35 points) Judith Johnson is always on the lookout for entreprencurial opportunities. Living in Six Mile, South Carolina, she recognizes that the nearest airport is 50 miles away. Judith estimates that, on average, there are about 45 people from Six Mile (and its vicinity) who need rides to or from the airport each day. To help them, Judith is considering leasing a 10-passenger van and offering a limousine service between Six Mile and the airport. There would be four trips per day: a morning trip and an evening trip to the airport, and a morning trip and an evening trip from the airport After researching the issue carcefully, Judith sets some operating guidelines for her problem and estimates the following parameters for each trip .Reservations for a trip can be made up to 12 hours in advance, by paying a nonrefundable S10 deposit. Judith will accept reservations up to her reservation limit (which this simulation model will help her decide). The ticket price is $35 per passenger per trip. Passengers with reservations must pay $25 balance at the start of the trip. e number of reservations requested each trip follows a discrete uniform distribution ed . Th between 7 and 14. Judith will, of course, reject a reservation request if she has reach her reservation limit. The probability that a person with a reservation shows up for the trip is 0.80. In o . words, 20% ofpeople with reservations do not show up. Anyone who does not show up forfeits the $10 deposit. If the number of passengers who show up exceeds 10 (the passenger capacity of the van), . alternate arrangements must be made to get these extra people to the airport. This will cost Judith $75 per person. That is, Judith will lose $40 (-$75 $35) per overbooked person. . The number of walk-up passengers (i.e., passengers without reservations) for a trip has the following discrete general distribution: probability of zero walk-ups is 0.30, probability of one walk-up is 0.45, and probability of two walk-ups is 0.25. Judith does not anticipate that there will ever be more than two walk-ups per trip. Walk-up passengers pay $50 per trip. However, Judith does not have to make alternate arrangements for these passengers if her van is full The total cost per trip (to or from the airport) to Judith is $100. Note that due to the possibility of walk-up passengers on the return trip, Judith has to make a trip to the . airport even if she has no passengers on that trip. Judith wants to find out how many reservations she should accept in order to maximize her average profit per trip. Specifically, she is considering accepting 10, 11, 12, 13, or 14 reservations. Please e-mail your completed files to lan.luo@wsu.edu. This assignment may be completed in a group of up to four people. Please state in the email message the names of all persons turning in this assignment. Please put "MgtOp 470 Homework 6" followed by the name of the person who sent the email in the Subject of the email. I. a. (35 points) Judith Johnson is always on the lookout for entreprencurial opportunities. Living in Six Mile, South Carolina, she recognizes that the nearest airport is 50 miles away. Judith estimates that, on average, there are about 45 people from Six Mile (and its vicinity) who need rides to or from the airport each day. To help them, Judith is considering leasing a 10-passenger van and offering a limousine service between Six Mile and the airport. There would be four trips per day: a morning trip and an evening trip to the airport, and a morning trip and an evening trip from the airport After researching the issue carcefully, Judith sets some operating guidelines for her problem and estimates the following parameters for each trip .Reservations for a trip can be made up to 12 hours in advance, by paying a nonrefundable S10 deposit. Judith will accept reservations up to her reservation limit (which this simulation model will help her decide). The ticket price is $35 per passenger per trip. Passengers with reservations must pay $25 balance at the start of the trip. e number of reservations requested each trip follows a discrete uniform distribution ed . Th between 7 and 14. Judith will, of course, reject a reservation request if she has reach her reservation limit. The probability that a person with a reservation shows up for the trip is 0.80. In o . words, 20% ofpeople with reservations do not show up. Anyone who does not show up forfeits the $10 deposit. If the number of passengers who show up exceeds 10 (the passenger capacity of the van), . alternate arrangements must be made to get these extra people to the airport. This will cost Judith $75 per person. That is, Judith will lose $40 (-$75 $35) per overbooked person. . The number of walk-up passengers (i.e., passengers without reservations) for a trip has the following discrete general distribution: probability of zero walk-ups is 0.30, probability of one walk-up is 0.45, and probability of two walk-ups is 0.25. Judith does not anticipate that there will ever be more than two walk-ups per trip. Walk-up passengers pay $50 per trip. However, Judith does not have to make alternate arrangements for these passengers if her van is full The total cost per trip (to or from the airport) to Judith is $100. Note that due to the possibility of walk-up passengers on the return trip, Judith has to make a trip to the . airport even if she has no passengers on that trip. Judith wants to find out how many reservations she should accept in order to maximize her average profit per trip. Specifically, she is considering accepting 10, 11, 12, 13, or 14 reservations