Please explain to me clearly and show how to do the two suppositions in the (question) file. Please take a look at the (notes) file and see the material up to the questions will be needed to answer the question.

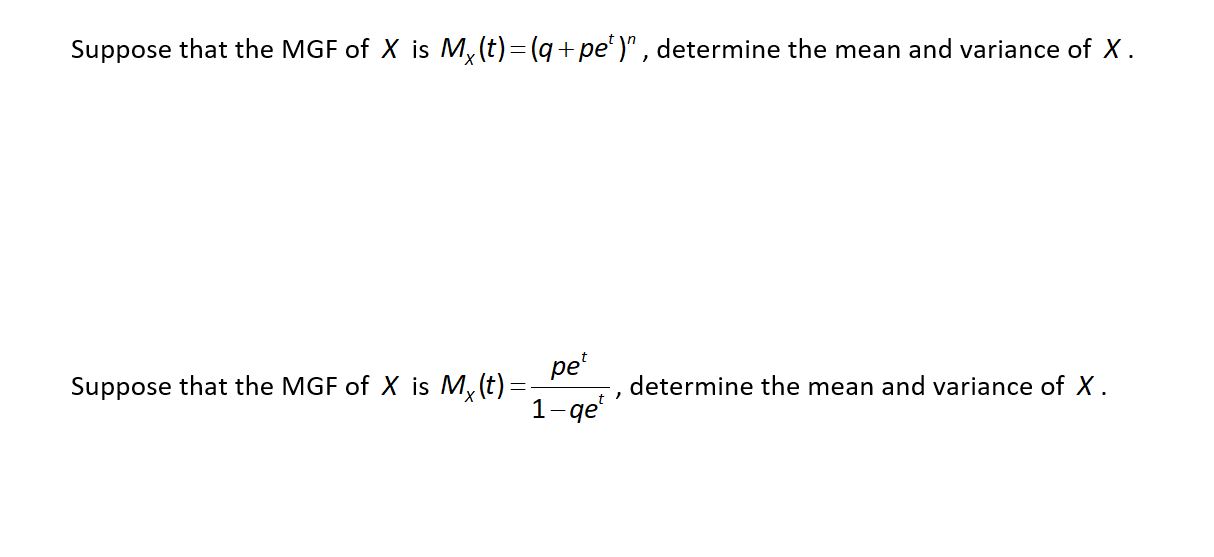
1 Chapter 3: Discrete Random Variables In this chapter we will define a discrete random variable, study properties of random variables and study several common and useful discrete random variables. Discrete: Finite or countable collection Variable: A measured quantity that is allowed to take on a variety of values. Random: Not determined by us From our past experience we know what a variable is. A variable is a quantity that can vary. We usually use a letter to denote the variable (quantity). We use a letter because a number just wouldn't work since numbers can't vary. Example: A company makes widgets and sells them for $10 each. They can make as many widgets as the want. The number of widgets is therefore not a fixed number but a variable chosen by the company. Thus, we would want to use a variable (say x) to represent the number of widgets made. The revenue generated by these widgets is also a variable (say y) that is dependent on the number of widgets that we make. In life there are many quantities that vary (variables) and the value that the variable takes on is not chosen by us or anybody else. Here are some examples: The length of time it takes a person run to run a mile tomorrow The number of spots we will see after a die is rolled Your weight tomorrow morning The number of customers that will come to our restaurant tomorrow for lunch The number of patients that will be admitted to the emergency room today How long it will take us to drive to work today All of these quantities are variables since they can take on many possible values. The difference between these variables and the number of widgets made in the example above is that the actual value of our variable is not picked by us or anybody else. It is random. That is, the value is somewhat a matter of chance. There are any possibilities, but we do not pick the value. So the value eventually given to these variables is random and depends on probability. 2 3.1 What is a Random Variable Definition: Let S be a discrete sample space from some experiment. A Random Variable is a function from a sample space into the real numbers. Random variables are always denoted with a capital letter. Usually, we would want our random variable to be some meaningful quantity. Example: Our experiment is to roll two dice. Our sample space in the collection of all permutations of the integers 1 through 6. Some meaningful random variables might be\" X1 equals the sum of the two dice. We can write what our random variable X1 does to outcomes in S in our familiar functional notation: , , etc. X1 (1,3) 4 X1 (2,2) 4 X1 (3,1) 4 We can define other random variables on our sample space: X2 X3 equals the larger of the two values on the dice. equals the larger number minus the smaller number. As in algebra or calculus, we can use subscripts to distinguish one function from another. Example: Determine X1 (4,5) 3 Example: Determine Example: Determine X2 (4,5) X3 (4,5) Example: Suppose that we are going to toss a coin 3 times. Let Determine the values of X count the number of heads tossed. , and . X (HHH) X (TTH) X (HTT ) So, our random variable takes outcomes from the sample space of a random experiment and turns them into real numbers. Thus, we now have a collection of real numbers that have been randomly chosen. These real numbers can be seen as a sample space from an experiment. We would now like to define probabilities to these numbers in a natural way. We define P( X x ) Ai S ; X ( Ai ) x P(Ai ) Consider our rolling two dice experiment with the random variable X1 that equals the total number of spots rolled. Each of our 36 outcomes in the sample space has probability 1/36. We now determine the probability that our random variable takes on the value 4. Since the only outcomes that satisfy Ai S X1 (Ai ) 4 are (1,3), (2,2) and (3,1) we have P( X1 4) Certainly 1 1 1 3 36 36 36 36 P( X1 2.75) 0 since our random variable does not map any outcomes into the value 2.75. 4 Definition: The Support of a discrete random variable is defined to be where x such that 0 P( X x) , denotes all real numbers. Example: The support of the random variable random variable X2 is S 1,2,3,4,5,6 X1 is S 2,3,4,5,6,7,8,9,10,11,12 . The support of the . Example: Determine the support of the random variable X3 . Example: A coin is tossed three times. Let X count the number of heads tossed. Determine the support of . X Notice that the support can be thought of as a sample space. Since we have endowed the support with a probability function, the support along with the collection of probabilities, is a probability space. 3.2 The Distribution Our experiment is to toss a coin three times. Let toss? Than is, what value will X X count the number of heads. How many heads will we take on? The answer is \"We don't know - it's random\". We can however come up with a collection of ordered pairs of numbers that detail what can happen and what are the associated probabilities. So, we will make a list (or create a formula) that associates the probability of occurrence for each value in our support. Definition: For a random variable X , the Probability Mass Function (pmf) is a function that assigns the probability of occurrence to each value in the support. We denote this function f (x) . 5 Our pmf can be written out in table format or in the form of a formula. Consider our experiment where we toss three coins and an experiment where we roll a single die. x 0 1 2 3 f(x) 1/8 3/8 3/8 1/8 n x x 3 1 1 f ( x) x 2 2 for x 0,1,2,3 x 1 2 3 4 5 6 f(x) 1/6 1/6 1/6 1/6 1/6 1/6 f (x ) 1 for x 1,2,3,4,5,6 6 When we write out our pmf in functional form, we want to be sure to include the support. It should be noted that writing out the pmf in tabular form carries the exact same information as it does in functional form. We could also graph each pmf as done below. This format also carries the same information. pmf of Rolling a Die pmf of Tossing 3 Coins and X = Number of Heads 0.22 0.375 0.20 0.18 0.250 0.16 0.14 0.125 0.12 0 1 2 C4 3 1 2 3 4 5 6 C1 Certainly, if the support was a larger set, this graph could be very useful. We purposely use dots with a line projected down. The probabilities hare are point masses and are not spread over an interval on the x-axis. There is a mass at 0, 1, 2 and 3. As always, the total mass (probability) is equal to one. In all three formats, the total probability of 1 is distributed over the support. We therefore refer the information about the support and associated probabilities as the Distribution. The stick figure graph given above carries more information when we have more than just a few values that the random variable X can take on. Consider the visualization of four random variables given below. The graph can contain much more intuitive information than we would get by looking at a table of values. While we will use the table of values to determine answers to probability questions, the graph can give us a feeling of the distribution. 6 In each of these graphs we can instantly get a feeling for the distribution. If we looked at random variables with many more possible x-values, we might see even more information that might not be seen when looking at a table of values (see below). The pmf is one way to convey the distribution (the story of probability) of a random variable. A second method for writing out the distribution is the Cumulative Distribution Function (CDF). 7 Definition: For a random variable F ( x) P ( X x ) X , we define the Cumulative Distribution Function (CDF) as . The information contained in the pmf and CDF are identical. Neither tells us more about the story of probability than the other, so both are considered the distribution. The distribution considered in its CDF format can be very handy for discrete random variables and is a necessity for continuous random variables that we will discuss in the next chapter. For our two examples, the CDFs are given below. x 0 1 2 3 x 1 2 3 4 5 6 F(x) 1/8 4/8 7/8 1 F(x) 1/6 2/6 3/6 4/6 5/6 1 We get from the pmf to the CDF by addition and from the CDF to the pmf by subtraction. When we study continuous distributions, can you guess how we get from one to the other? When we are discussing discrete random variables, a graph of the CDF is not as useful as the pmf. We can however see some things from these sample graphs. Theorem: The CDF is right continuous. Theorem: lim F (x) 1 x Theorem: lim F (x) 0 x Theorem: P(A X B) F (B) F (A ) 8 Example: Determine P(2 X 4) for the single die experiment. P(2 X 4) F (4) F (2 ) 4 1 3 6 6 6 For many of the distributions that we will study in the next few sections, we will be using CDF charts with a support being a subset of the integers. Therefore, we would be wise to master using CDF charts. Example: The pmf for some random variable X is given below. Determine the CDF. x f(x) 1 F(x) x f(x) F(x) .15 1 .15 .15 2 .11 2 .11 .26 3 .09 3 .09 .35 4 .35 4 .35 .70 5 .17 5 .17 .87 6 .13 6 .13 1.00 To get from the pmf to the CDF we add all probability at or below each value in the support. When determining f (4) to F (3) . This asks for all values of X less than 4 and including 4. P( X 4) F (3) , we just add The chart values increase each stop of the way and terminate at 1 in the finite support case and have a limit of 1 in the countable case. P( X 4) not including 4. F (4) F (4) This asks for all values of X less than 4 but 9 P(6 X ) This asks for all values of X greater than 6 and including 6. P(6 X ) 1 F (5) This asks for all values of X greater than 6 not including 6. 1 F (6) P(4 X 8) F (8) F (4 ) F (8) F (3) 3.3 The Expected Value of a Random Variable Las Vegas, Nevada - where dreams come true (for casino owners). Casinos, just on the strip, have averaged over $6,000,000,000 ($6 billion) per year from 2005 through 2016. Are they cheating? Or, do they just expect to win? Why would they expect to win? Maybe they have the edge. Each time anybody places a bet, they are doing a random experiment and the amount won or lost on the bet is a number. Thus, we have a random variable that randomly chooses how much you win or lose. 10 What would it mean for the casino to have the edge? Does it mean that they have a better chance of winning than the player? In some cases, yes, but not in all. Let's look at some game examples and decide if we would like to place such a bet. These are not actual games in Las Vegas. Example: We roll a single die. If we roll a 1, we win $10. For all other rolls, we lose $1. In this bet, we would lose far more often than we would win. But when we win, we make much more than we lose on the times that we do lose. If everything goes according to plan, like in Disneyland, we would win $10 exactly one-sixth of the time and lose $1 exactly five-sixths of the time. Overall, we would show a profit. Of course, this isn't Disneyland and things might not go as planned, but theoretically, we would expect to win. We would want to take this bet. Example: Consider a bet that we have a 50% chance of winning. In this game, if we win the bet, we collect $10 profit. If we lose the bet, we pay $11. In this game, we will win as often as we lose in a perfect world. The bad part is clear. Each win ($10) does not make up for each loss ($11). In the long run, we would expect to lose money. We would not want to play this game. In this same example, if we only pay $10.01 when we lose, the game is not nearly as unbalanced. Example: In this game, when we win, we are paid $10. When we lose, we pay $10. Would we want to play this game? If you have already answered (Yes or No), you have answered too soon. You don't know what the probability of winning is. If your theoretical chance of winning is 50%, this is a fair game and playing is fine. If your theoretical chance of winning is 49%, the game is unfair, but not too unfair. If your theoretical chance of winning is 40%, the game is very unfair and playing would be very bad. Based on these examples, we see that your theoretical expectation is a combination of your probability of winning along with what you get paid when you win and what you pay when you lose. Definition: The mean of a discrete random variable xf (x) X , is defined by the formula (provided the sum converges) xSupport If we are in a situation where we have two random variables, say X and Y subscripts to denote which mean is connected to which random variable: , we will make use of X and Y . There are times where we prefer a different name and notation for the mean of a random variable. We will use the phrase Expected Value of a random variable interchangeably with the Mean of a random variable. Our new associated notation for the expected value is . E[ X ] 11 Remember that a random variable chooses numbers. We should thing of the mean of a random variable as what the data average , , would be if we collect a huge amount of data. x Example: A single die is rolled and X denotes the number of spots viewed. The mean of X can be determined using the above formula. 1 1 1 1 1 1 (1) (2) (3) (4) (5) (6) 3.5 6 6 6 6 6 6 Obviously, we will never roll a 3.5. But, that is the theoretical mean or average. Consider rolling the die 60 times in Disneyland. Since everything goes according to plan, we will get exactly 10 of each of the six possibilities. Our data average would be x 10(1) 10(2) 10(3) 10(4) 10(5) 10(6) 3.5 60 Example: Consider spinning the spinner below. What is the expected value of the spinner? We could make our pmf chart and then calculate the mean of the random variable. x f(x) 1 .1 2 .2 3 .3 4 .4 (1)(.1) (2)(.2) (3)(.3) (4)(.4) 3.0 Suppose that we had a game that had 300 spaces on it. We move as many spaces as we spin on the spinner. Since our expected number on the spinner is 3.0, we would expect the game to take about 100 spins. Example: Consider spinning the spinner below. What is the expected value of the spinner? We could make our pmf chart and then calculate the mean of the random variable. x f(x) 1 .4 2 .3 3 .2 Determine the expected value of 4 .1 X . About how many spins would it take to get through our 300 spaces on our board game? 12 Not all random variables have a finite mean. Let 1 1 1 f ( x) for x 1,2,3,L x (x 1) x x 1 X be a random variable with pmf . You should verify that this sums to 1. To determine the mean of this random variable, we calculate 1 1 x x(x 1) x 1 (x 1) x 1 . Since this series diverges, our random variable does not have a finite mean. Consider f (x) k(1 / (n ^2 1) on the integers 3.4 The Expected Value of a Function of a Random Variable Often times in the real world, we wish to look at a function of our variables - or transform them. Changing feet into meters, Fahrenheit into centigrade, etc. In this section we seek to determine the expected value of this new variable. If we transform a random variable by some function , it X Y g( X ) should be clear that Y is a random variable. Theorem: Given a random variable Proof: X and the transformation , . Y aX b E[Y ] E[aX b] aE[ X ] b E[aX b] (ax b) f (x) (ax) f (x) (b) f ( x) a xf (x) b f ( x) aE[ X ] b a X b Thus, the expected value of a random variable is a linear operator. 13 Example: If a random variable Y 2 X 3 11 or X has mean 4 , determine the mean of Y , where Y 2X 3 E[Y ] E[2 X 3] 2E[ X ] 3 11 If we think about this last example, it seems like a no brainer that it is true. The average score is 4. I double everybody's score. The new average is 8. I know add 3 to everybody's doubled score. The new average is 11. In this linear case, notice if we consider Y g( X ) 2 X 3 , then E[Y ] E[g( X )] 2 X 3 g(E[ X ]) would naturally wonder if that statement always holds. That is, will it always be true that If E[Y ] g(E[ X ]) the expected value of -2 fX ( x) 1/8 xfX (x) -1/8 -1 1/8 -2/8 0 2/8 0 1 1/8 2 X ? To determine y E[Y ] X with pmf given below. We now let , we will find 4 fY (y) 1/8 yfY (y) 4/8 1 1/8 1/8 0 2/8 0 1/8 1 1/8 1/8 2/8 4 3 1/8 3/8 4 1/8 4/8 E[ X ] 7 / 8 We see that that Y g( X ) then . The answer is no, this is not always true. How will we show this? Suppose that we have a discrete random variable x . We YX 2 and then compute y 0 yfY (y) 0 1 2/8 2/8 4 2/8 8/8 1/8 9 1/8 9/8 1/8 4/8 16 1/8 16/8 9 1/8 9/8 16 1/8 16/8 . What is E[Y ] yfY (y ) fY (y) 2/8 . E[Y ] 35 / 8 E[Y ] 35 / 8 49 35 E[ X ]2 E[ X 2 ] E[Y ] 64 8 E[Y ] g(E[ X ]) fY (y) Y X2 . So, we have our counter example and in general, it is not true . We do however see something helpful when looking at the first two groupings in the 14 above table. We see that the probabilities are identical and that each y-value is the square of the x-value. This leads us to the following theorem that will help us determine E[Y ] Theorem: Given a discrete random variable X and a function , . Y g( X ) E[Y ] E[g( X )] g(x) fX (x) The theorem is much bigger than it seems. It allows us to determine the expected value of a transformation of a random variable without determining the distribution of the new random variable. We easily found in the above problem. With continuous random variables, it can often be difficult fY (y) to determine fY (y) , so this will be huge when we get to continuous random variables. 3.5 Some Important Functions of a Random Variable (Moments and Variance) Definition: The Variance of a discrete random variable 2 (x )2 f (x) X is defined by the formula (provided the sum converges). Alternatively, 2 E[(x )2 ] . xSupport Definition: The Standard Deviation of a random variable, denoted by Note that we can consider the function Y g( X ) (x )2 , is defined by . Then the variance is just 2 E[g( X )] E[Y ] . In a data set, we use the standard deviation of the data set to denote a measure of the variation of the data. The standard deviation of a random variable does the same thing. It gives us a measure of how spread out the support is. Example: Determine the standard deviation for rolling a single die. 15 1 1 17.5 2 (x 3.5)2 (1 3.5)2 (2 3.5)2 L (6 3.5)2 2.916667 6 6 6 x 1 6 Theorem: Proof: . So 1.7078 . 2 E[(x )2 ] E[ X 2 ] E 2 [ X ] E[(x )2 ] (x )2 f (x) (x 2 2 x 2 ) f (x) x 2 f (x) 2 xf (x) f (x) E[ X 2 ] 2 E[ X 2 ] E 2 [ X ] Example: Recalculate the standard deviation of a single die using the theorem. 1 91 2 (12 22 32 42 52 62 ) 3.52 3.52 2.916667 6 6 In general, this theorem allows a much easier calculation than the definition. Soon, we will see problems where this formula is a necessity. Not all random variables have a finite variance. We saw earlier that we can have a random variable that does not have a finite mean. We can also have a random variable with finite mean, but not finite variance. k f (x) 3 for x 1,2,3,L x , where k is the value that makes random variable has finite mean since f (x) a pmf. That is, so that k k k 2 E[ X ] x 3 2 x x 1 x 6 x 1 variance of our random variable, we need to determine E[ X 2 ] . So, this random variable has finite mean but not finite variance. k 1 3 x 1 x . This , which is finite. To determine the k k E[ X ] x 3 x x 1 x x 1 2 2 which diverges. 16 The E[ X ] is often called the first moment of Definition: The kth moment of X X and is defined to be E[ X 2 ] is called the second moment of X . E[ X k ] These moments are important features of a random variable. Sometimes they are called the moments about the origin and then moments about the mean would be defined as . E[( X )k ] 3.5 The Moment Generating Function We now look at a very special function of our random variable : . Why that function? Let's X Y e Xt investigate. We are not at appoint where we are trying to find the distribution of our transformation, but we are interested in the expected value of our transformation. So we will consider the . E[Y ] Definition: We define the Moment Generating Function of a random variable MX (t ) E[e Xt ] e xt f (x) some open interval of Theorem: , provided t 0 MX '(t ) t 0 E[ X ] , except X to b the sum converges for all values of t in possibly at t 0 itself. 17 Proof: MX '(t ) E[e ] ' e f (x) ' xe f (x) Xt Theorem: Proof: MX ''(t ) t 0 xt xt . Plugging in t 0 yields: MX '(0) xf ( x) E[ X ] E[ X 2 ] MX ''(t ) MX '(t ) ' xe xt f (x ) ' x 2e xt f (x) . Plugging in t 0 yields: MX ''(0) x 2 f (x) E[ X 2 ] Our generalized theorem is then. Theorem: MX (k ) (t ) t 0 E[ X k ] What should we call this function that generates the moments of the distribution (random variable)? Not all random variables have a MGF. Suppose that the MGF of Suppose that the MGF of X X is is MX (t ) (q pet )n pet MX (t ) 1 qet , determine the mean and variance of , determine the mean and variance of X X . . \f