Please, explanation of how the sketch of B was made.Thanks

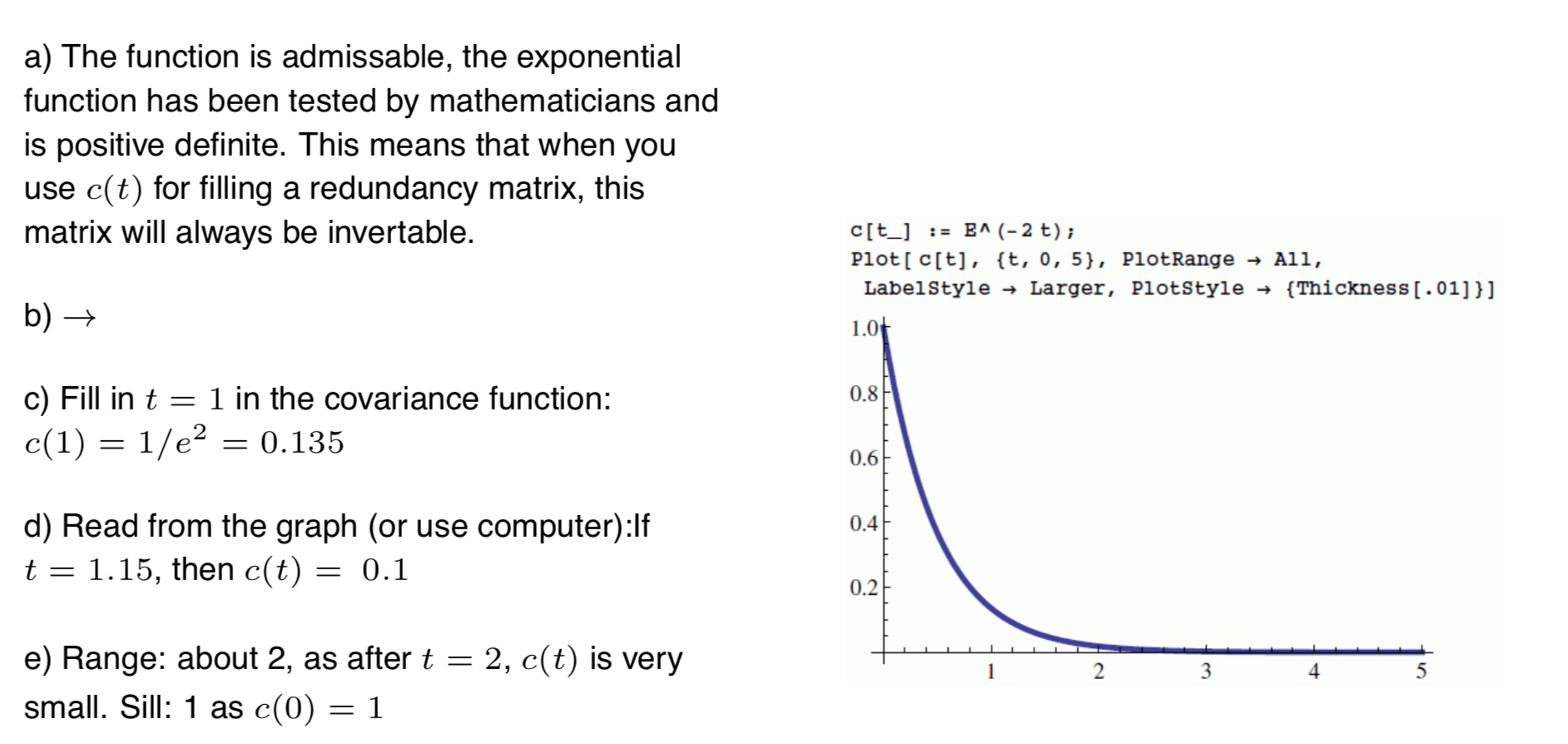
4 3 2 0 0 4 6 8 Exercise 8.1 In the figure, the points p = (1, 1), p2 = (2, 2), p3 = (4,3), p4 = (4.5, 4), and p5 = (6, 2.5) are shown. Think of these points as the result of measuring some signal as function of time in seconds. In addition a covariance function c(t) = e-2t is given a). Is this covariance function admissable? Why? b). Sketch c(t). What are its extrema? c). What is the covariance between two observations that are 1 second apart? d). After what time drops c(t) below one tenth of its maximal value? e). How would you define the range and sill for this covariance function? a) The function is admissable, the exponential function has been tested by mathematicians and is positive definite. This means that when you use c(t) for filling a redundancy matrix, this matrix will always be invertable. c[t_] := B^(-2 t); Plot[ C[t], {t, 0,5}, PlotRange All, LabelStyle Larger, PlotStyle + {Thickness [.01]}] 1.00 b) 0.8 c) Fill in t = 1 in the covariance function: c(1) = 1/e2 = 0.135 0.6 0.4 d) Read from the graph (or use computer):If t = 1.15, then c(t) = 0.1 0.2 2 3 4 5 e) Range: about 2, as after t = 2, c(t) is very small. Sill: 1 as c(0) = 1 4 3 2 0 0 4 6 8 Exercise 8.1 In the figure, the points p = (1, 1), p2 = (2, 2), p3 = (4,3), p4 = (4.5, 4), and p5 = (6, 2.5) are shown. Think of these points as the result of measuring some signal as function of time in seconds. In addition a covariance function c(t) = e-2t is given a). Is this covariance function admissable? Why? b). Sketch c(t). What are its extrema? c). What is the covariance between two observations that are 1 second apart? d). After what time drops c(t) below one tenth of its maximal value? e). How would you define the range and sill for this covariance function? a) The function is admissable, the exponential function has been tested by mathematicians and is positive definite. This means that when you use c(t) for filling a redundancy matrix, this matrix will always be invertable. c[t_] := B^(-2 t); Plot[ C[t], {t, 0,5}, PlotRange All, LabelStyle Larger, PlotStyle + {Thickness [.01]}] 1.00 b) 0.8 c) Fill in t = 1 in the covariance function: c(1) = 1/e2 = 0.135 0.6 0.4 d) Read from the graph (or use computer):If t = 1.15, then c(t) = 0.1 0.2 2 3 4 5 e) Range: about 2, as after t = 2, c(t) is very small. Sill: 1 as c(0) = 1