Please help and explain

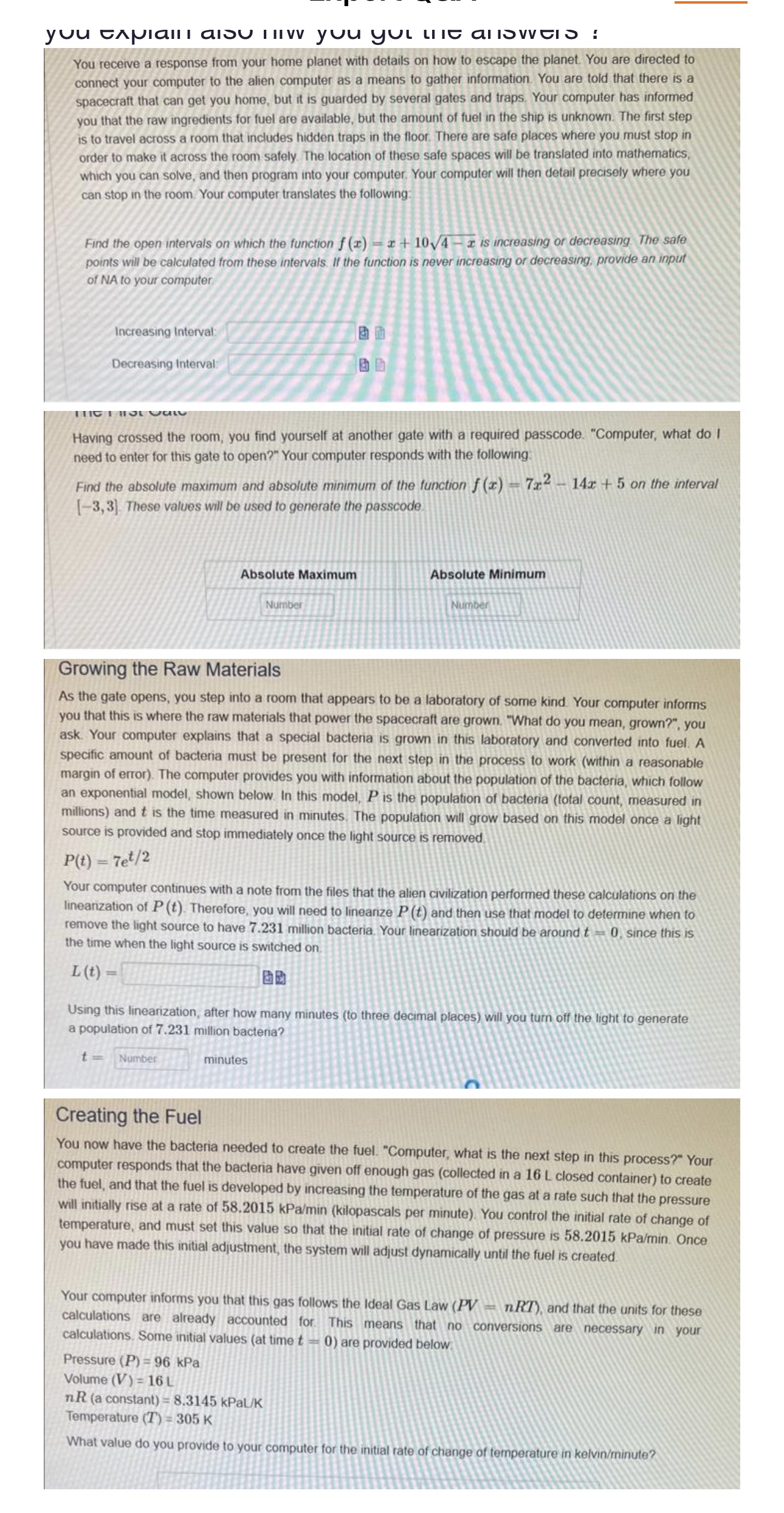
you CAPIallI also HIV you yUL LITE alloveIS ! You receive a response from your home planet with details on how to escape the planet. You are directed to connect your computer to the alien computer as a means to gather information. You are told that there is a spacecraft that can get you home, but it is guarded by several gates and traps. Your computer has informed you that the raw ingredients for fuel are available, but the amount of fuel in the ship is unknown. The first step is to travel across a room that includes hidden traps in the floor. There are safe places where you must stop in order to make it across the room safely. The location of these safe spaces will be translated into mathematics, which you can solve, and then program into your computer. Your computer will then detail precisely where you can stop in the room Your computer translates the following: Find the open intervals on which the function f (x) - x + 10v4 - x is increasing or decreasing The safe points will be calculated from these intervals. If the function is never increasing or decreasing, provide an input of NA to your computer Increasing Interval: Decreasing Interval: Having crossed the room, you find yourself at another gate with a required passcode. "Computer, what do I need to enter for this gate to open?" Your computer responds with the following: Find the absolute maximum and absolute minimum of the function f (x) -7x- -14x + 5 on the interval [-3,3). These values will be used to generate the passcode Absolute Maximum Absolute Minimum Number Growing the Raw Materials As the gate opens, you step into a room that appears to be a laboratory of some kind. Your computer informs you that this is where the raw materials that power the spacecraft are grown. "What do you mean, grown?", you ask. Your computer explains that a special bacteria is grown in this laboratory and converted into fuel. A specific amount of bacteria must be present for the next step in the process to work (within a reasonable margin of error). The computer provides you with information about the population of the bacteria, which follow an exponential model, shown below. In this model, P is the population of bacteria (total count, measured in millions) and t is the time measured in minutes. The population will grow based on this model once a light source is provided and stop immediately once the light source is removed P(t) = 7et/2 Your computer continues with a note from the files that the alien civilization performed these calculations on the linearization of P (t). Therefore, you will need to linearize P (t) and then use that model to determine when to remove the light source to have 7.231 million bacteria. Your linearization should be around t - 0, since this is the time when the light source is switched on L (t) - Using this linearization, after how many minutes (to three decimal places) off the light to generate a population of 7.231 million bacteria? Number minutes Creating the Fuel You now have the bacteria needed to create the fuel. "Computer, what is the next step in this process?" Your computer responds that the bacteria have given off enough gas (collected in a 16 L closed container) to create the fuel, and that the fuel is developed by increasing the temperature of the gas at a rate such that the pressure will initially rise at a rate of 58.2015 kPa/min (kilopascals per minute). You control the initial rate of change of temperature, and must set this value so that the initial rate of change of pressure is 58.2015 kPa/min. Once you have made this initial adjustment, the system will adjust dynamically until the fuel is created. Your computer informs you that this gas follows the Ideal Gas Law (PV - n RT), and that the units for these calculations are already accounted for This means that no conversions are necessary in your calculations. Some initial values (at time t - 0) are provided below: Pressure (P) #96 kPa Volume (V) = 16 L n R (a constant) - 8.3145 kPaL/K Temperature (T) = 305 K What value do you provide to your computer fo f temperature in kelvin/minute