please help!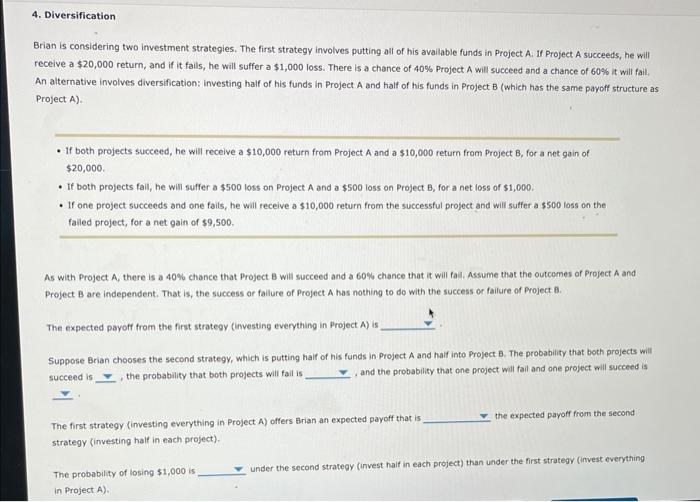

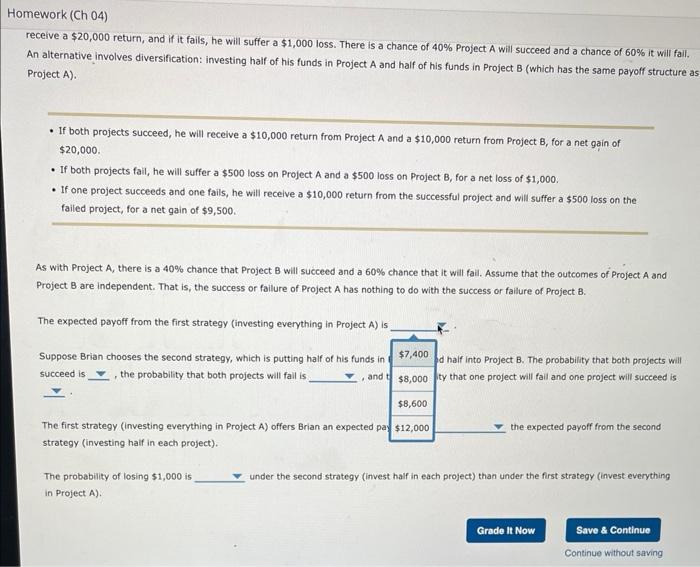
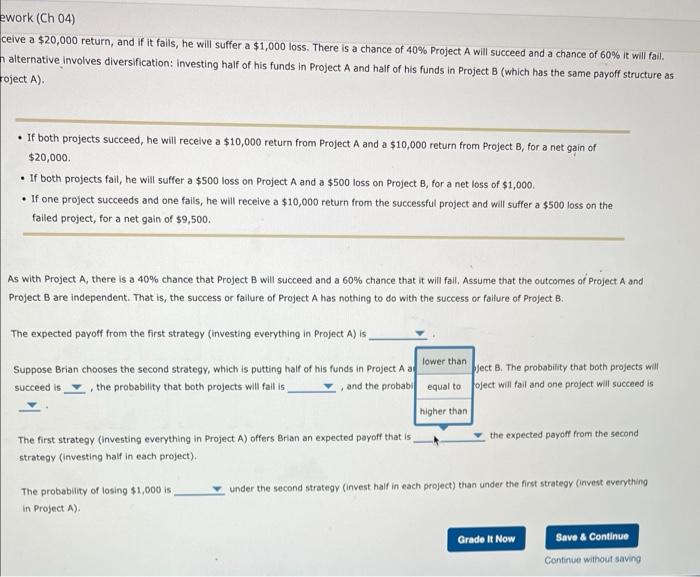
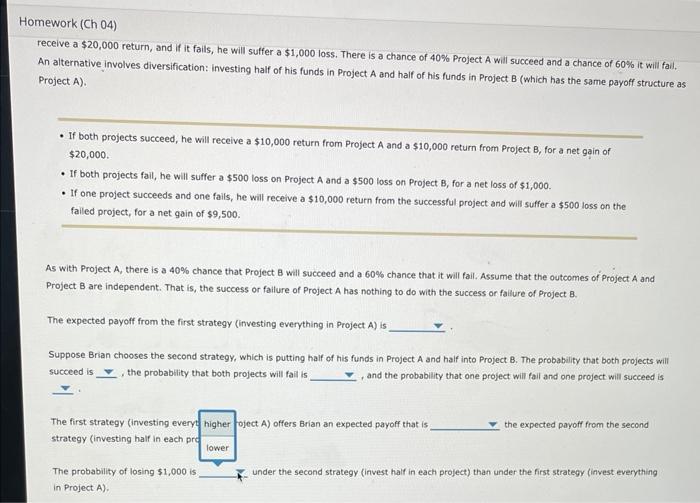
Brian is considering two investment strategies. The first strategy involves putting all of his avallable funds in Project A. If Project A succeeds, he will receive a $20,000 return, and if it fails, he will suffer a $1,000 loss. There is a chance of 40% Project A will succeed and a chance of 60% it will fail. An alternative involves diversification: investing half of his funds in Project A and half of his funds in Project B (which has the same payoff structure as Project A). - If both projects succeed, he will receive a $10,000 return from Project A and a $10,000 return from Project B, for a net gain of $20,000 - If both projects fall, he will suffer a $500 loss on Project A and a $500 loss on Project B, for a net loss of $1,000. - If one project succeeds and one fails, he will receive a $10,000 return from the successful project and will sulfer a $500 foss on the falled project, for a net gain of $9,500. As with Project A, there is a 40% chance that Project B will succeed and a 60% chance that it will fall. Assume that the outcomes of Project A and Project B are independent. That is, the success or fallure of Project A has nothing to do with the success or failure of Project B. The expected payoff from the first strategy (investing everything in Project A ) is Suppose Brian chooses the second strategy, which is putting half of his funds in Project A and half into Project B. The probability that both projects will succeed is , the probability that both projects will fail is and the probability that one project will fail and one project will succeed is The first strategy (investing everything in Project A ) offers Brian an expected payoff that is the expected payoff from the second strategy (investing half in each project). The probability of losing $1,000 is under the second strategy (invest haif in each project) than under the first strategy (invest everything in Project A). receive a $20,000 retum, and if it fails, he will suffer a $1,000 loss. There is a chance of 40% Project A will succeed and a chance of 60% it will fall. An alternative involves diversification: investing half of his funds in Project A and half of his funds in Project B (which has the same payoff structure a Project A). - If both projects succeed, he will receive a $10,000 return from Project A and a $10,000 return from Project B, for a net 9 ain of $20,000. - If both projects fail, he will suffer a $500 loss on Project A and a $500 loss on Project B, for a net loss of $1,000. - If one project succeeds and one fails, he will receive a $10,000 return from the successful project and will suffer a $500 loss on the failed project, for a net gain of $9,500. As with Project A, there is a 40% chance that Project B will succeed and a 60% chance that it will fail. Assume that the outcomes of Project A and Project B are independent. That is, the success or failure of Project A has nothing to do with the success or fallure of Project B. The expected payoff from the first strategy (investing everything in Project A) is Suppose Brian chooses the second strategy, which is putting half of his funds in succeed is , the probability that both projects will fall is $7,400 and half into Project B. The probability that both projects will The first strategy (investing everything in Project A) offers Brian an expected pay strategy (investing half in each project). The probability of losing $1,000 is under the second strategy (invest half in each project) than under the first strategy (invest everything in Project A). Continue without saving Ceive a $20,000 return, and if it fails, he will suffer a $1,000 loss. There is a chance of 40% Project A will succeed and a chance of 60% it will fail. alternative involves diversification: Investing half of his funds in Project A and half of his funds in Project B (which has the same payoff structure as oject A). - If both projects succeed, he will receive a $10,000 return from Project A and a $10,000 return from Project B, for a net gain of $20,000. - If both projects fail, he will suffer a $500 loss on Project A and a $500 loss on Project B, for a net loss of $1,000. - If one project succeeds and one fails, he will receive a $10,000 return from the successful project and will suffer a $500 loss on the failed project, for a net gain of $9,500. As with Project A, there is a 40% chance that Project B will succeed and a 60% chance that it will fall. Assume that the outcomes of Project A and Project B are independent. That is, the success or failure of Project A has nothing to do with the success or fallure of Project B. The expected payoff from the first strategy (investing everything in Project A) is Suppose Brian chooses the second strategy, which is putting half of his funds in Project A a succeed is , the probability that both projects will fall is, , and the probabil probability that both projects will The first strategy (investing everything in Project A) offers Brian an expected payoff that is the expected payoff from the second strategy (investing half in each project). The probability of losing $1,000 is under the second strategy (invest half in each project) than under the first strategy (invest everything in Project A ). mework (Ch 04) receive a $20,000 return, and if it fails, he will suffer a $1,000 loss. There is a chance of 40% Project A will succeed and a chance of 60% it will fail, An alternative involves diversification: investing half of his funds in Project A and half of his funds in Project B (which has the same payoff structure as Project A). - If both projects succeed, he will receive a $10,000 return from Project A and a $10,000 return from Project B, for a net gain of $20,000. - If both projects fail, he will suffer a $500 loss on Project A and a $500 loss on Project B, for a net loss of $1,000. - If one project succeeds and one fails, he will receive a $10,000 return from the successful project and will suffer a $500 loss on the failed project, for a net gain of $9,500. A5 with Project A, there is a 40% chance that Project B will succeed and a 60% chance that it will fail. Assume that the outcomes of Project A and Project B are independent. That is, the success or fallure of Project A has nothing to do with the success or failure of Project B. The expected payoff from the first strategy (investing everything in Project A) is Suppose Brian chooses the second strategy, which is putting half of his funds in Project A and half into Project B. The probability that both projects will succeed is , the probability that both projects will faili is, and the probablity that one project will fail and one project will succeed is The first strategy (investing every oject A) offers Brian an expected payoff that is the expected payoff from the second strategy (investing half in each pri The probability of losing $1,000 is under the second strategy (invest half in each project) than under the first strategy (invest everything in Project A)