please help, I cannot figure out how to get the number from the tree and also the u=1.0748 I do not know how to get that one either
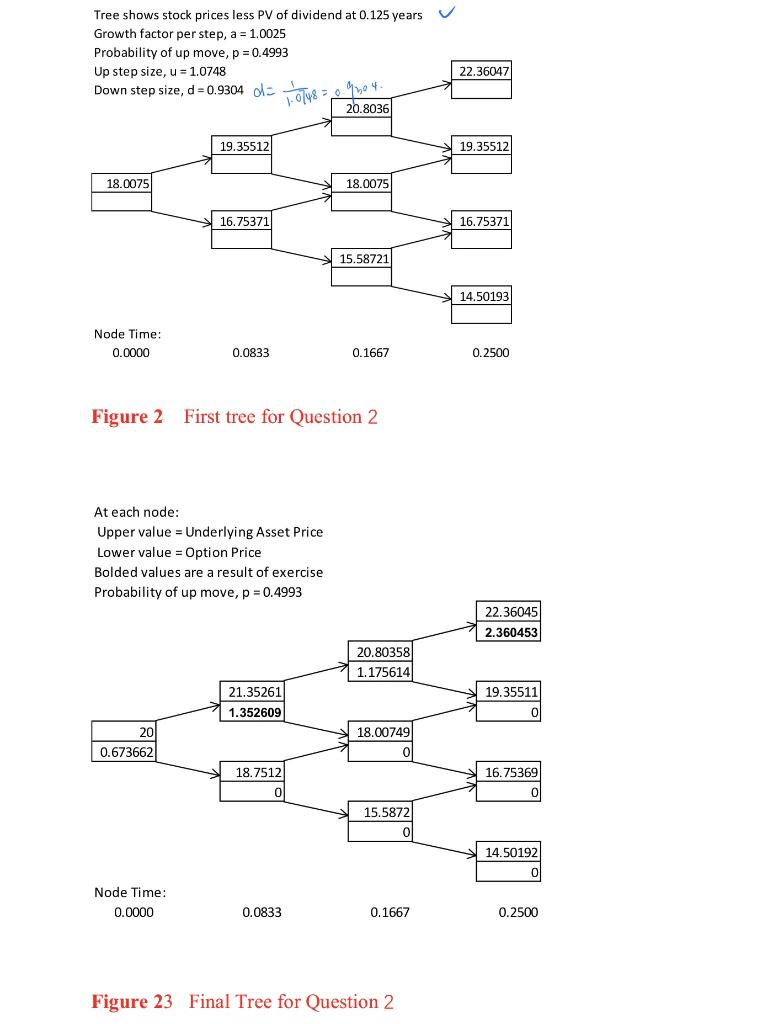
Question 2 A three-month American call option on a stock has a strike price of $20. The stock price is $20, the risk-free rate is 3% per annum, and the volatility is 25% per annum. A dividend of $2 is expected in 1.5 months. Use a three-step binomial tree to calculate the option price. -0.030.125 In this case the present value of the dividend is 2e = 1.9925. We first build a tree for S=20-1.9925=18.0075, K = 20, r=0.03, o=0.25, and T = 0.25 with At=0.08333. This gives Figure 2. For nodes between times 0 and 1.5 months we then add the present value of the dividend to the stock price. The result is the tree in Figure 3. The price of the option calculated from the latter tree is 0.6737. Tree shows stock prices less PV of dividend at 0.125 years Growth factor per step, a = 1.0025 Probability of up move, p = 0.4993 Up step size, u = 1.0748 Down step size, d = 0.9304 = -~-0748 = 0 950 4- 20.8036 19.35512 18.0075 18.0075 16.75371 15.58721 Node Time: 0.0000 0.0833 0.1667 Figure 2 First tree for Question 2 At each node: Upper value = Underlying Asset Price Lower value = Option Price Bolded values are a result of exercise Probability of up move, p = 0.4993 20.80358 1.175614 21.35261 1.352609 20 18.00749 0.673662 0 18.7512 15.5872 Node Time: 0.0000 0.0833 0.1667 Figure 23 Final Tree for Question 2 22.36047 19.35512 16.75371 14.50193 0.2500 22.36045 2.360453 19.35511 16.75369 14.50192 0 0.2500 Question 2 A three-month American call option on a stock has a strike price of $20. The stock price is $20, the risk-free rate is 3% per annum, and the volatility is 25% per annum. A dividend of $2 is expected in 1.5 months. Use a three-step binomial tree to calculate the option price. -0.030.125 In this case the present value of the dividend is 2e = 1.9925. We first build a tree for S=20-1.9925=18.0075, K = 20, r=0.03, o=0.25, and T = 0.25 with At=0.08333. This gives Figure 2. For nodes between times 0 and 1.5 months we then add the present value of the dividend to the stock price. The result is the tree in Figure 3. The price of the option calculated from the latter tree is 0.6737. Tree shows stock prices less PV of dividend at 0.125 years Growth factor per step, a = 1.0025 Probability of up move, p = 0.4993 Up step size, u = 1.0748 Down step size, d = 0.9304 = -~-0748 = 0 950 4- 20.8036 19.35512 18.0075 18.0075 16.75371 15.58721 Node Time: 0.0000 0.0833 0.1667 Figure 2 First tree for Question 2 At each node: Upper value = Underlying Asset Price Lower value = Option Price Bolded values are a result of exercise Probability of up move, p = 0.4993 20.80358 1.175614 21.35261 1.352609 20 18.00749 0.673662 0 18.7512 15.5872 Node Time: 0.0000 0.0833 0.1667 Figure 23 Final Tree for Question 2 22.36047 19.35512 16.75371 14.50193 0.2500 22.36045 2.360453 19.35511 16.75369 14.50192 0 0.2500
