- please help. I stuck at question 6-7-8-9-10 this is my home work due on this week. Please try your best. thank you
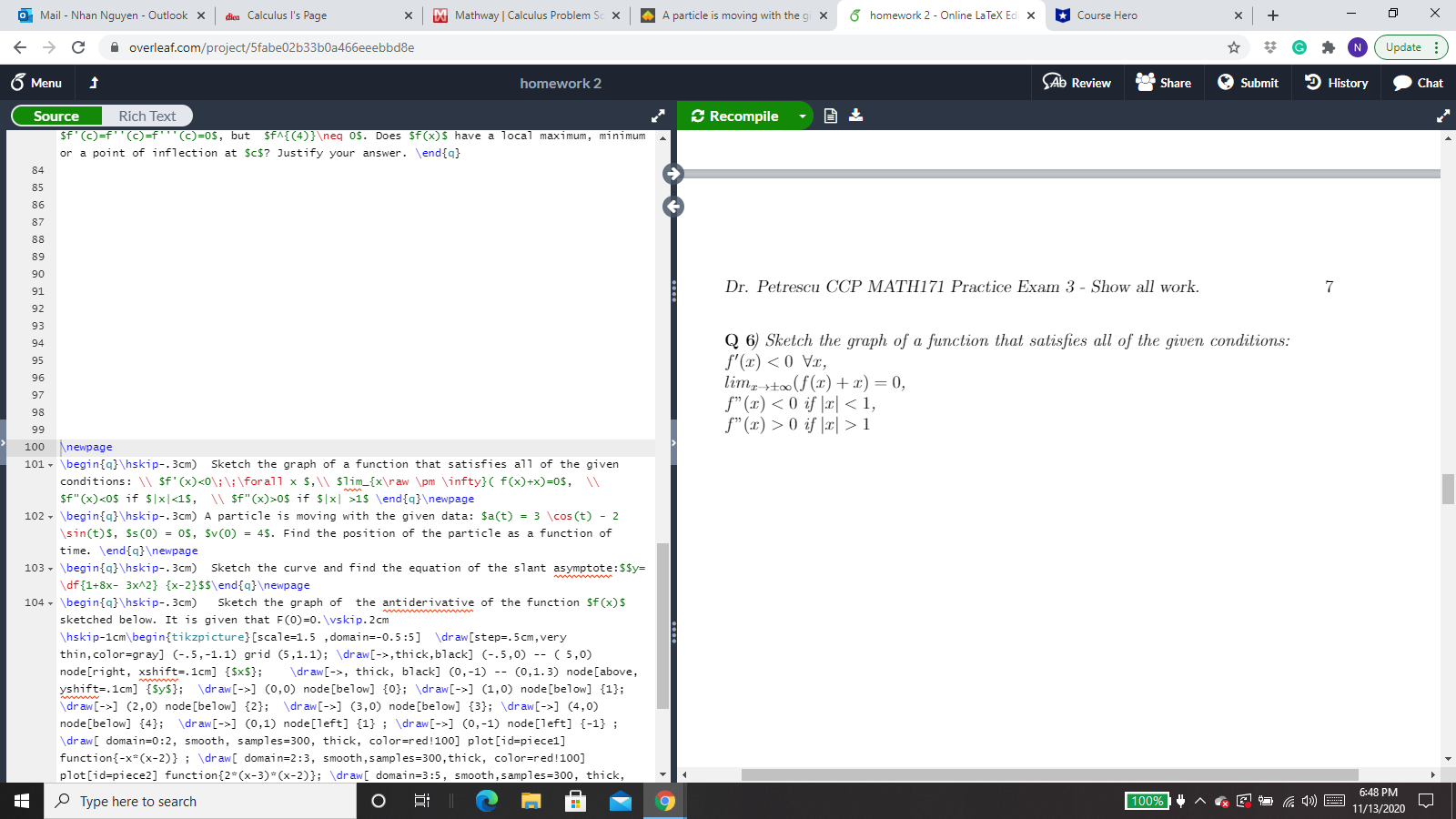
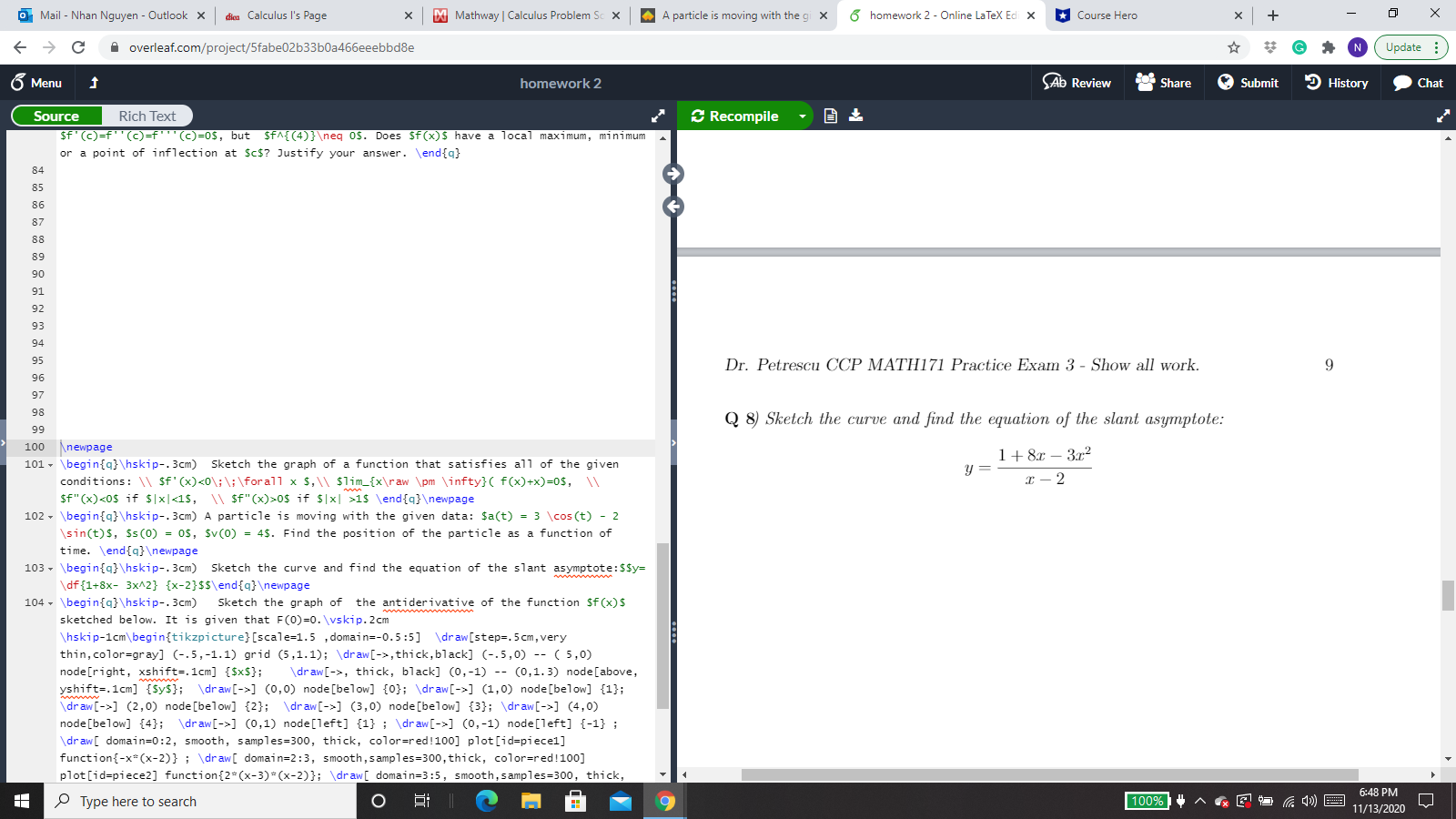
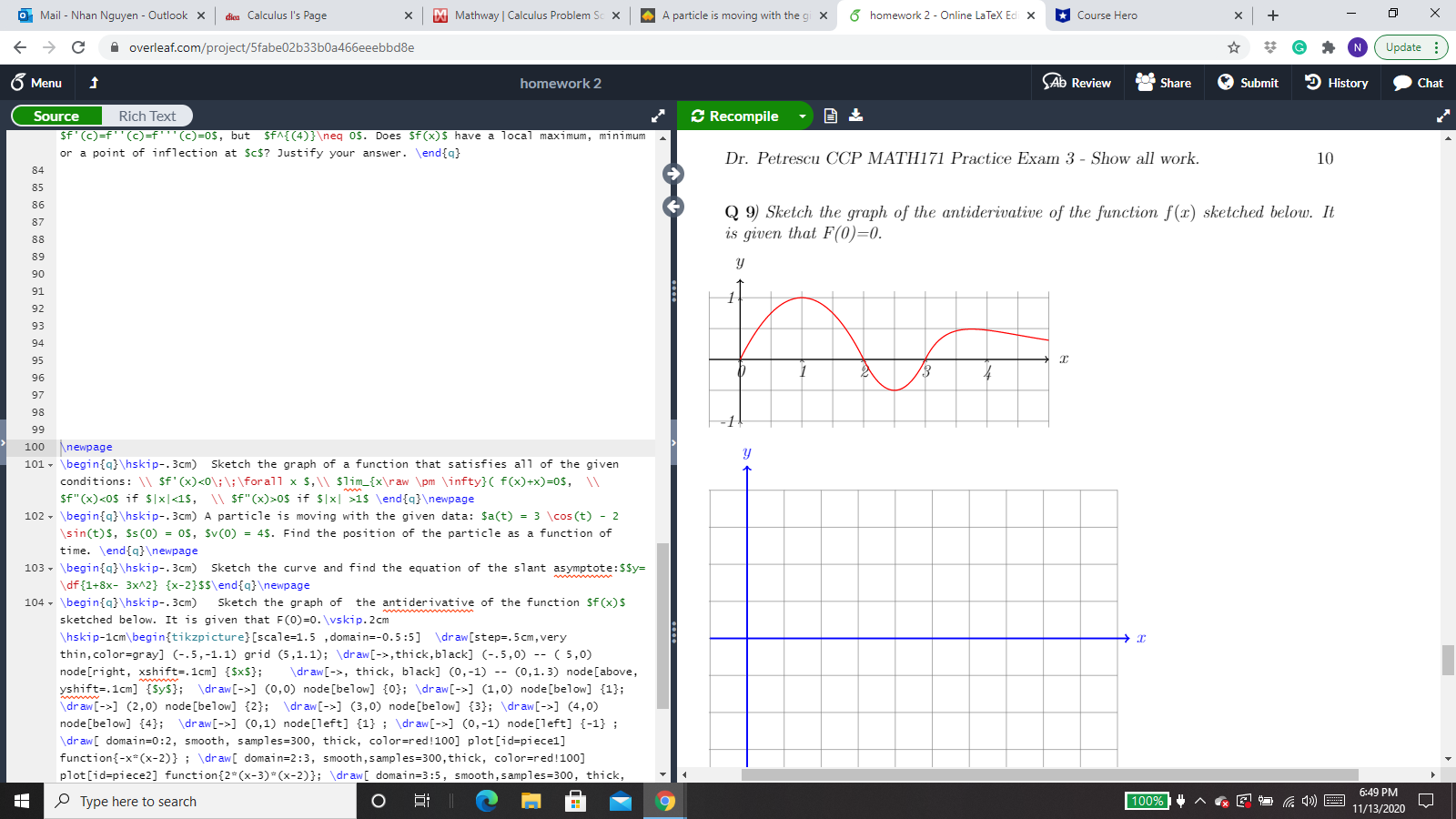
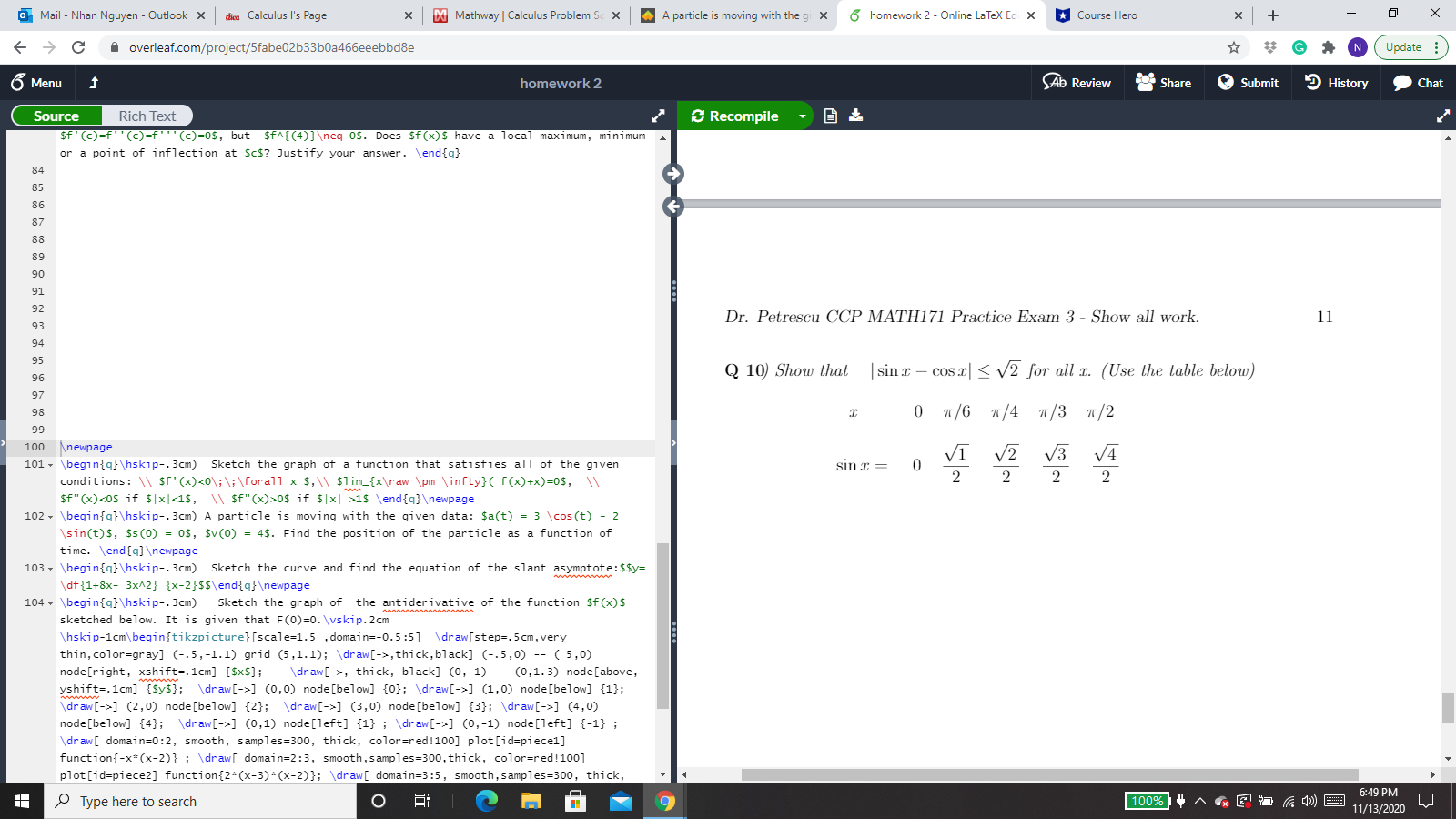
Mail - Nhan Nguyen - Outlook X dica Calculus I's Page X Do Mathway | Calculus Problem Sc X A particle is moving with the gi X 6 homework 2 - Online LaTeX Ed X * Course Hero X + X C A overleaf.com/project/5fabe02b33b0a46beeebbdBe GAN Update : 6 Menu homework 2 Ab Review Share Submit History Chat Source Rich Text Recompile if (c)=f" (c)=f' "(c)=0$, but $fA{(4)}\ eq os. Does Sf(x)$ have a local maximum, minimum or a point of inflection at $c$? Justify your answer. \\endfa} 84 85 86 87 88 89 Dr. Petrescu CCP MATH171 Practice Exam 3 - Show all work. 7 Q 6) Sketch the graph of a function that satisfies all of the given conditions: 96 f'(x) 0 if (x] > 1 100 Anewpage 101 * \\begin{q}\\hskip-. 3cm) Sketch the graph of a function that satisfies all of the given conditions: \\\\ sf' (x)0$ if $|x| >15 \\end{q}\ ewpage 102 - \\begin{q} \\hskip-. 3cm) A particle is moving with the given data: $a(t) = 3 \\cos(t) - 2 sin(t)$, $s(0) = 0$, $v(0) = 4$. Find the position of the particle as a function of time. \\end{q) \ ewpage 103 * \\begin{q}\\hskip-. 3cm) Sketch the curve and find the equation of the slant asymptote: $$y= df {1+8x- 3x42} {x-2}$5\\end{q}\ ewpage 104 \\begin{q}\\hskip-. 3cm) Sketch the graph of the antiderivative of the function $f (x)$ sketched below. It is given that F(0)=0. \\vskip. 2cm \\hskip-1cm\\begin{tikzpicture} [scale=1.5 , domain=-0.5:5] \\draw[step=. 5 cm, very thin, color=gray] (-.5, -1.1) grid (5,1.1); \\draw[->, thick, black] (-.5,0) -- ( 5,0) node [right, xshift=. 1cm] {$x$}; \\draw[->, thick, black] (0,-1) -- (0,1.3) node[above, yshift=.1cm] {$y$}; \\draw[->] (0,0) node[below] {0}; \\draw[->] (1,0) node[below] {1}; draw [->] (2,0) node[below] {2}; \\draw[->] (3,0) node[below] {3}; \\draw[->] (4,0) node[below] {4}; \\draw[->] (0,1) node[left] {1} ; \\draw[->] (0,-1) node[left] {-1} ; (draw [ domain=0:2, smooth, samples=300, thick, color=red!100] plot[id=piece1] function{-x=(x-2)} ; \\draw[ domain=2:3, smooth, samples=300, thick, color=red!100] plot [id=piece2] function{2*(x-3) =(x-2)}; \\draw[ domain=3:5, smooth, samples=300, thick, Type here to search O 9 6:48 PM 11/13/2020Mail - Nhan Nguyen - Outlook X dica Calculus I's Page X Do Mathway | Calculus Problem Sc X A particle is moving with the gi X 6 homework 2 - Online LaTeX Ed X * Course Hero X + X C A overleaf.com/project/5fabe02b33b0a46beeebbdBe GAN Update : 6 Menu homework 2 Ab Review Share Submit History Chat Source Rich Text Recompile if (c)=f" (c)=f' "(c)=0$, but $fA{(4)}\ eq 05. Does Sf (x)$ have a local maximum, minimum or a point of inflection at $c$? Justify your answer. \\endfa} 84 85 86 87 88 89 96 Dr. Petrescu CCP MATH171 Practice Exam 3 - Show all work. 9 97 98 Q 8) Sketch the curve and find the equation of the slant asymptote: 100 Anewpage 101 * \\begin{q}\\hskip-. 3cm) Sketch the graph of a function that satisfies all of the given y = 1+ 8x - 3x2 conditions: \\\\ sf' (x)0$ if $|x| >15 \\end{q}\ ewpage 102 - \\begin{q} \\hskip-. 3cm) A particle is moving with the given data: $a(t) = 3 \\cos(t) - 2 sin(t)$, $s(0) = 0$, $v(0) = 4$. Find the position of the particle as a function of time. \\end{q) \ ewpage 103 * \\begin{q}\\hskip-. 3cm) Sketch the curve and find the equation of the slant asymptote: $$y= df {1+8x- 3x42} {x-2}$5\\end{q}\ ewpage 104 \\begin{q}\\hskip-. 3cm) Sketch the graph of the antiderivative of the function $f (x)$ sketched below. It is given that F(0)=0. \\vskip. 2cm \\hskip-1cm\\begin{tikzpicture} [scale=1.5 , domain=-0.5:5] \\draw[step=. 5 cm, very thin, color=gray] (-.5, -1.1) grid (5,1.1); \\draw[->, thick, black] (-.5,0) -- ( 5,0) node [right, xshift=. 1cm] {$x$}; \\draw[->, thick, black] (0,-1) -- (0,1.3) node[above, yshift=.1cm] {$y$}; \\draw[->] (0,0) node[below] {0}; \\draw[->] (1,0) node[below] {1}; draw [->] (2,0) node[below] {2}; \\draw[->] (3,0) node[below] {3}; \\draw[->] (4,0) node[below] {4}; \\draw[->] (0,1) node[left] {1} ; \\draw[->] (0,-1) node[left] {-1} ; (draw [ domain=0:2, smooth, samples=300, thick, color=red!100] plot[id=piece1] function{-x=(x-2)} ; \\draw[ domain=2:3, smooth, samples=300, thick, color=red!100] plot [id=piece2] function{2*(x-3) =(x-2)}; \\draw[ domain=3:5, smooth, samples=300, thick, Type here to search O 9 6:48 PM 11/13/2020Mail - Nhan Nguyen - Outlook X dica Calculus I's Page X Do Mathway | Calculus Problem Sc X A particle is moving with the gi X 6 homework 2 - Online LaTeX Edi X * Course Hero X + X C A overleaf.com/project/5fabe02b33b0a46beeebbdBe GAN Update : 6 Menu homework 2 Ab Review Share Submit History Chat Source Rich Text Recompile if (c)=f" (c)=f' "(c)=0s, but sfA{(4)}\ eq 05. Does Sf (x)$ have a local maximum, minimum or a point of inflection at $c$? Justify your answer. \\endfa} 84 Dr. Petrescu CCP MATH171 Practice Exam 3 - Show all work. 10 85 86 87 Q 9) Sketch the graph of the antiderivative of the function f(x) sketched below. It 88 is given that F(0)=0. 89 y 96 97 98 100 Anewpage 101 * \\begin{q}\\hskip-. 3cm) Sketch the graph of a function that satisfies all of the given y conditions: \\\\ sf' (x)0$ if $|x| >15 \\end{q}\ ewpage 102 - \\begin{q} \\hskip-. 3cm) A particle is moving with the given data: $a(t) = 3 \\cos(t) - 2 sin(t)$, $s(0) = 0$, $v(0) = 4$. Find the position of the particle as a function of time. \\end{q) \ ewpage 103 * \\begin{q}\\hskip-. 3cm) Sketch the curve and find the equation of the slant asymptote: $$y= df {1+8x- 3x42} {x-2}$5\\end{q}\ ewpage 104 \\begin{q}\\hskip-. 3cm) Sketch the graph of the antiderivative of the function $f (x)$ sketched below. It is given that F(0)=0. \\vskip. 2cm \\hskip-1cm\\begin{tikzpicture} [scale=1.5 , domain=-0.5:5] \\draw[step=. 5cm, very thin, color=gray] (-.5, -1.1) grid (5,1.1); \\draw[->, thick, black] (-.5,0) -- ( 5,0) node [right, xshift=. 1cm] {$x$}; \\draw[->, thick, black] (0,-1) -- (0,1.3) node[above, yshift=.1cm] {$y$}; \\draw[->] (0,0) node[below] {0}; \\draw[->] (1,0) node[below] {1}; draw [->] (2,0) node[below] {2}; \\draw[->] (3,0) node[below] {3}; \\draw[->] (4,0) node[below] {4}; \\draw[->] (0,1) node[left] {1} ; \\draw[->] (0,-1) node[left] {-1} ; (draw [ domain=0:2, smooth, samples=300, thick, color=red!100] plot[id=piece1] function{-x=(x-2)} ; \\draw[ domain=2:3, smooth, samples=300, thick, color=red!100] plot [id=piece2] function{2*(x-3) =(x-2)}; \\draw[ domain=3:5, smooth, samples=300, thick, Type here to search O 9 6:49 PM 11/13/2020Mail - Nhan Nguyen - Outlook X dica Calculus I's Page X Do Mathway | Calculus Problem Sc X A particle is moving with the gi X 6 homework 2 - Online LaTex Ed X * Course Hero X + X C A overleaf.com/project/5fabe02b33b0a46beeebbdBe GAN Update : 6 Menu homework 2 Ab Review Share Submit History Chat Source Rich Text Recompile if (c)=f" (c)=f' "(c)=0$, but sfA{(4)}\ eq 05. Does Sf(x)$ have a local maximum, minimum or a point of inflection at $c$? Justify your answer. \\endfa} 84 85 86 87 88 89 Dr. Petrescu CCP MATH171 Practice Exam 3 - Show all work. 11 96 Q 10) Show that | sinx - cosx| 0$ if $|x| >15 \\end{q}\ ewpage 102 - \\begin{q} \\hskip-. 3cm) A particle is moving with the given data: $a(t) = 3 \\cos(t) - 2 sin(t)$, $s(0) = 0$, $v(0) = 4$. Find the position of the particle as a function of time. \\end{q) \ ewpage 103 * \\begin{q}\\hskip-. 3cm) Sketch the curve and find the equation of the slant asymptote: $$y= df {1+8x- 3x42} {x-2}$5\\end{q}\ ewpage 104 \\begin{q}\\hskip-. 3cm) Sketch the graph of the antiderivative of the function $f (x)$ sketched below. It is given that F(0)=0. \\vskip. 2cm \\hskip-1cm\\begin{tikzpicture} [scale=1.5 , domain=-0.5:5] \\draw[step=. 5 cm, very thin, color=gray] (-.5, -1.1) grid (5,1.1); \\draw[->, thick, black] (-.5,0) -- ( 5,0) node [right, xshift=. 1cm] {$x$}; \\draw[->, thick, black] (0,-1) -- (0,1.3) node[above, yshift=.1cm] {$y$}; \\draw[->] (0,0) node[below] {0}; \\draw[->] (1,0) node[below] {1}; draw [->] (2,0) node[below] {2}; \\draw[->] (3,0) node[below] {3}; \\draw[->] (4,0) node[below] {4}; \\draw[->] (0,1) node[left] {1} ; \\draw[->] (0,-1) node[left] {-1} ; (draw [ domain=0:2, smooth, samples=300, thick, color=red!100] plot[id=piece1] function{-x=(x-2)} ; \\draw[ domain=2:3, smooth, samples=300, thick, color=red!100] plot [id=piece2] function{2*(x-3) =(x-2)}; \\draw[ domain=3:5, smooth, samples=300, thick, Type here to search O 9 100%$1718 6:49 PM 11/13/2020