Please help!!!

In this lab you will restructure your geometry code to make it more object oriented. You also will adapt your Geometry class code from a previous assignment and add it to other classes. You will implement an intersection method that computes the point of intersection of two points. Finally, you will ensure that all your code works properly by testing it interactively within a graphical application.

Create a new project

Create a new project and add the following files to your project:

Point.java

Line.java

VisualGeometry.java

The VisualGeometry.java file contains the main method and all the necessary code to manage the graphical interface. You should not modify the contents of VisualGeometry.java. Your task is to add code to the first two files, Point.java and Line.java.

When you are finished with this assignment you will upload the completed Point.java and Line.java files to eClass.

Complete the Point class

Complete the distance method that computes the distance between a given point and another point object. If p1 and p2 are Point objects, the following statement:

double d = p1.distance(p2);

will assign to the variable d the distance between points p1 and p2 .

Complete the Line class

Complete the two overloaded constructors: one accepts two Point objects, and the other accepts two double-precision floating-point values representing the line's slope and intercept.

Complete the slope method that returns the slope of the line. As before, if the line is vertical, the slope method should return Double.POSITIVE_INFINITY.

Complete the intercept method that returns the intercept of the line. As before, if the line is vertical, the intercept method should return the line's x intercept; otherwise, the method returns the line's y intercept.

Complete the intersection method that returns the point of intersection of a given line object with another line object. If ln1 and ln2 are Line objects, the following statement:

Point p = ln1.intersection(ln2);

will assign the point of intersection of the two lines to the Point object p, if such a point exists.

Be sure your method works properly if one of the two lines is vertical.

If the lines do not have a single point of intersection, the method should return null. Client code can check for this to see if there is a valid intersection point. Parallel lines have no single point of intersection.

How do you compute the point of intersection of two lines?

If the two lines have the same slope, there is no single point of intersection. The method returns null in that case.

If neither line is vertical, we have a pair of equations that look like

y = m₁x + b₁ y = m₂x + b₂

Since both righthand expressions equal y, set them equal to each other:

m₁x + b₁ = m₂x + b₂

and solve for x:

m1x - m2x + b1	=	m2x - m2x + b2
m1x - m2x + b1	=	b2
m1x - m2x + b1 - b1	=	b2 - b1
m1x - m2x	=	b2 - b1
(m1 - m2)x	=	b2 - b1
x	=	(b2 - b1)/ (m1 - m2)

This final equation

x = (b₂ - b₁)/(m₁ - m₂)

serves as a formula to compute x. (In your Java code you need only be concerned with this final formula.) Once you have x you can plug it into either of the original equations to compute y. This (x,y) point is the point of intersection of the two lines.

If one of the lines is vertical, you cannot use the above formula. Attempting to perform arithmetic with Double.POSITIVE_INFINITY will not produce a useful result. Since you know the x-intercept of the vertical line, you can deduce the x coordinate of the intersection directly from the vertical line. You then can plug this x value into the equation for the non-vertical line to compute the intersection point's y coordinate.

Be sure that your code works correctly whether the first line or the second line that is vertical.

Your intersection method must contain conditional logic to decide from among the possibilities listed above.

You are free to implement the internal details of the Line class as you see fit. These internal details must be inaccessible to clients; therefore, any instance variables you add must be declared private. You could use two points as instance variables to maintain the state of a Line object. This would be okay, but a better approach is to precompute the line's slope and intercept in the constructor and store these values in instance variables. (This approach would make writing the slope and intercept methods a trivial task.) Regardless, your Line objects must participate correctly with the other code provided. Be prepared to justify your design decision if asked about it.

Strategy

Before you modify Point.java or Line.java, ensure that the project builds and runs without any errors and without crashing. It should allow the user to add points and move them around. If the program does not allow the user to perform this minimal interaction, your project has a problem somewhere.

Until you correctly implement the intersection method, the lines will not draw properly. You should, however, be able to interact with the program without it crashing.

Keep things simple to begin with, and implement the typical case that does not involve vertical lines. Once you can see the red intersection point of the two lines, you should proceed to the case that involves vertical lines. In order for the application to extend the lines to the edges of the window, it must be able to compute the lines' intersection points with the imaginary lines that make up the horizontal edges of the window, (approximately y = 300 and y = 300) or the vertical edges of the window, (approximately x = 300 and x = 300). It calls your intersection method to compute these points. This is why the application cannot render the extended lines completely until you correctly implement the intersection method.

In the course of using the graphical application you may discover problems with one or more of your previous slope, intercept, or lineToString methods that the handful of tests from the previous assignment did not reveal. You should repair any problems you discover.

Additional remarks

You may have to fix errors in your existing methods if the new graphical client code reveals logic errors that were not uncovered by earlier tests.

The most common problem that students have is the application not drawing the lines as it should. This issue is most likely due to an incorrect and/or incomplete intersection method. The supplied graphical code depends on a correctly written intersection method to draw a line from one side of the window to the other. Since it is easy to experiment with all kinds of lines visually, your testing may reveal errors in your existing codethe intersection method cannot work correctly if the slope or intercept methods have issues. If you do not see any lines or lines are missing in certain situations, focus on correcting your intersection method. Pay particular attention to how you handle vertical lines.

Program execution

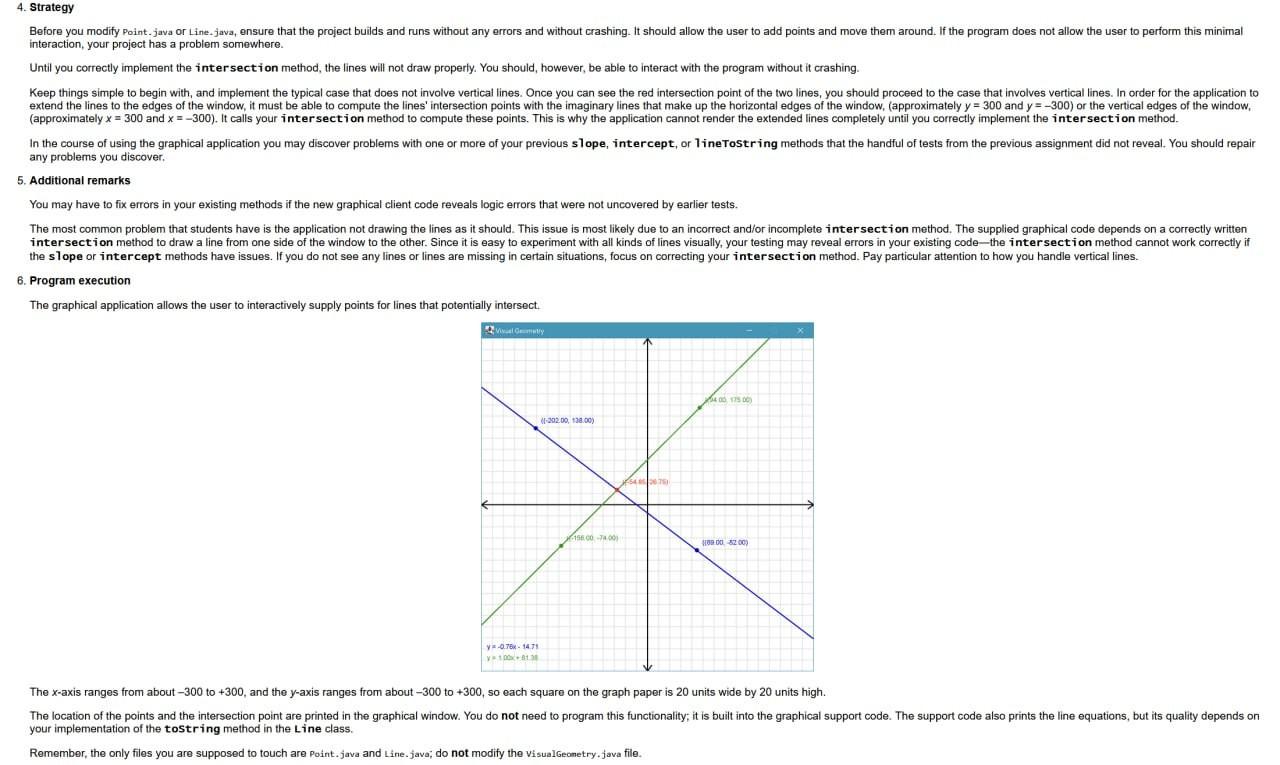
The graphical application allows the user to interactively supply points for lines that potentially intersect.

The x-axis ranges from about 300 to +300, and the y-axis ranges from about 300 to +300, so each square on the graph paper is 20 units wide by 20 units high.

The location of the points and the intersection point are printed in the graphical window. You do not need to program this functionality; it is built into the graphical support code. The support code also prints the line equations, but its quality depends on your implementation of the toString method in the Line class.

Remember, the only files you are supposed to touch are Point.java and Line.java; do not modify the VisualGeometry.java file.

Some useful interface shortcuts include:

If you wish to make a vertical line, press the V key after placing the first point of the line. The graphical interface will automatically position the line's second point to create a vertical line.

If you wish to make a horizontal line, press the H key after placing the first point of the line. The graphical interface will automatically position the line's second point to create a vertical line.

If you wish wish to clear all the points from the graph and make two new lines, press the Esc key.

Javadoc Documentation

All the public classes and methods in the provided Java source code are annotated with Java documentation comments. The javadoc tool automatically generates HTML documentation from Java documentation comments. You can read this HTML documentation with a web browser. Click this link to explore the results.

The Java documentation comments are helpful beyond their use in external documentation. Observe how the Eclipse IDE dynamically processes Java documentation comments by providing a pop-up help balloon when you hover over a class or method in the source code. This works only if the class or method has the necessary Java documentation comments.

Line	Represents a geometric line object.
Point	A geometric point is considered a "primitive" type, so the x and y fields are public.

Index

D I L P S T X Y All Classes|All Packages

D

distance(Point) - Method in class Point

Computes the distance between this point and another point.

I

intercept() - Method in class Line

Returns the line's intercept: y-axis intercept if the line is non-vertical x-axis intercept if the line is vertical

intersection(Line) - Method in class Line

Computes the point of intersection between this line and another line object.

L

Line - Class in

Represents a geometric line object.

Line(double, double) - Constructor for class Line

Makes a line object with a given slope and intercept

Line(Point, Point) - Constructor for class Line

Makes a line object that passes throught the given point objects.

P

Point - Class in

A geometric point is considered a "primitive" type, so the x and y fields are public.

Point(double, double) - Constructor for class Point

Make a point from (x, y) coordinates

S

slope() - Method in class Line

Returns the slope of the line

T

toString() - Method in class Line

Provides a human-readable string representation of the line; for example, y = mx + b form for non-vertical line and x = b for a vertical line.

toString() - Method in class Point

Produces a human-readable representation of the point.

X

x - Variable in class Point

The x coordinate of the point object

Y

y - Variable in class Point

The y coordinate of the point object

1. Lane.java

/ * Represents a geometric line object. All non-vertical lines have a slope and * y-axis intercept. All vertical lines have an infinite slope and * x-axis intercept. {@code Line} objects are immutable. */ public class Line {

/* * ####################################################### * IMPORTANT NOTE! * Add your instance variables here to maintain the the * state of a line object. * Line objects are immutable, so your instance variables * should be declared private to render them inaccessible * to clients. * ####################################################### */

/ * Test to see if two double-precision floating-point values are "equal." The * values are considered equal when their difference is small. * * @param a one of the values * @param b the other value * @param tolerance the small difference * @return True, if the two values are close enough to be considered equal; * otherwise, false */ private static boolean equals(double a, double b, double tolerance) { return a == b || Math.abs(a - b)

/ * Makes a line object with a given slope and intercept * * @param m the slope of the new line {@code Double.POSITIVE_INFINITY} for a * vertical line * @param b the y-axis intercept for a non-vertical line; the * x-axis intercept for a vertica line */ public Line(double m, double b) { // Add your code }

/ * Makes a line object that passes throught the given point objects. * * @param p1 one of the points on the line * @param p2 the other point on the line * @throws IllegalArgumentException if the two points are the same * @see Point */ public Line(Point p1, Point p2) { // Add your code }

/ * Returns the slope of the line * * @return the slope of the line, {@code Double.POSITIVE_INFINITY} if the line * is vertical */ public double slope() { // Replace with your code return 0.0; }

/ * Returns the line's intercept: *

*
• y-axis intercept if the line is non-vertical *
• x-axis intercept if the line is vertical *

* * @return the intercept of the line, x-axis intercept if the line is * vertical */ public double intercept() { // Replace with your code return 0.0; }

/ * Computes the point of intersection between this line and another line object. * * @param other the other line object * @return the point of intersectionm between this line ans the other line. * Returns {@code null} if the lines do not intersect * @see Point */ public Point intersection(Line other) { // Replace with your code return new Point(0, 0); }

/ * Provides a human-readable string representation of the line; for example, y = * mx + b form for non-vertical line and x = b for a vertical line. */ @Override public String toString() { // Replace with your code return "LINE EQUATION"; } }

2. Point.java

/ * A geometric point is considered a "primitive" type, so the {@code x} and * {@code y} fields are public. */ public class Point { / The x coordinate of the point object */ public double x;

/ The y coordinate of the point object */ public double y;

/ * Make a point from (x, y) coordinates * * @param x the x coordinate * @param y the y coordinate */ public Point(double x, double y) { this.x = x; this.y = y; }

/ * Computes the distance between this point and another point. * * @param other the other point to measure the distance to * @return the distance between this point and another point */ public double distance(Point other) { // Replace with your code return 0.0; }

/ * Produces a human-readable representation of the point. */ @Override public String toString() { return String.format("(%.2f, %.2f)", x, y); }

}

3. VisualGeometry.java

import javax.swing.JComponent; import javax.swing.JFrame; import javax.swing.JPanel; import javax.swing.SwingUtilities; import java.awt.*; import java.awt.event.KeyAdapter; import java.awt.event.KeyEvent; import java.awt.event.MouseAdapter; import java.awt.event.MouseEvent; import java.awt.geom.AffineTransform;

/ * An interactive visual application that allows the user to explore geometric * lines */ public class VisualGeometry {

@SuppressWarnings("serial") private static class GraphicalPanel extends JPanel { protected static final int NORMAL_OFFSET = 4; protected static final int ACTIVE_OFFSET = 8; protected static final int NORMAL_SIZE = 8; protected static final int ACTIVE_SIZE = 16; protected static final int CLOSENESS = 8; protected static final Color LIGHT_GRAY = new Color(220, 220, 220); protected static final Color DARK_GREEN = new Color(0, 150, 0); protected static final Color DARK_BLUE = new Color(0, 0, 200); protected Point point1 = null; protected Point point2 = null; protected Point point3 = null; protected Point point4 = null; protected Point intersectionPoint = null; protected Point activePoint = null; protected boolean isDragging = false;

protected Dimension dimension;

MouseAdapter mouseAdapter = new MouseAdapter() { @Override public void mousePressed(MouseEvent e) { if (activePoint != null) { isDragging = true; repaint(); } }

@Override public void mouseReleased(MouseEvent e) { int x = e.getX() - getWidth() / 2, y = getHeight() / 2 - e.getY(); if (point1 == null) { point1 = new Point(x, y); } else if (point2 == null) { point2 = new Point(x, y); } else if (point3 == null) { point3 = new Point(x, y); } else if (point4 == null) { point4 = new Point(x, y); } isDragging = false; repaint(); }

@Override public void mouseMoved(MouseEvent e) { if (!isDragging) { checkActive(e.getX() - getWidth() / 2, getHeight() / 2 - e.getY()); } repaint(); }

@Override public void mouseDragged(MouseEvent e) { if (isDragging && activePoint != null) { activePoint.x = e.getX() - getWidth() / 2; activePoint.y = getHeight() / 2 - e.getY(); } repaint(); } };

public GraphicalPanel(int width, int height) { setBackground(Color.WHITE); setLayout(null); addMouseListener(mouseAdapter); addMouseMotionListener(mouseAdapter); setFocusable(true); dimension = new Dimension(width, height); addKeyListener(new KeyAdapter() { @Override public void keyPressed(KeyEvent e) { super.keyTyped(e); switch (e.getKeyCode()) { case KeyEvent.VK_UP: System.out.println("You pressed the UP key"); break; case KeyEvent.VK_DOWN: System.out.println("You pressed the DOWN key"); break; case KeyEvent.VK_ESCAPE: point1 = point2 = point3 = point4 = activePoint = null; break; case KeyEvent.VK_V: if (point1 != null && point2 == null) { point2 = new Point(point1.x, getHeight() / 2); } else if (poin

computes the point of intersection of two points. Finally, you will ensure that all your code works properly by testing it interactively within a graphical application. 1. Create a new project Create a new project and add the following files to your project: P Pointijavi: 0 Lne. Java - VtsualGecnetry iava When you are finished with this assignment you will upload the completed Point. java and Line.java files to eClass. 2. Complete the Point class Complete the di stance method that computes the distance between a given point and another point object. If p1 and p2 are Point objects, the following statement: doubled=p1.distance(p2) will assign to the variable d the distance between points p1 and p2. 3. Complete the Line class Complete the two overloaded constructors: one accepts two Point objects, and the other accepts two double-precision floating-point values representing the line's slope and intercept. - Complete the slope method that returns the slope of the line. As before, if the line is vertical, the s7ope method should return Doub7e.POSITIVE_INFINITV. Complete the intersection method that returns the point of intersection of a given line object with another line object. If ln1 and 1n2 are Line objects, the following statement: will assign the point of intersection of the two lines to the Point object p, if such a point exists. Be sure your method works properly if one of the two lines is vertical. If the lines do not have a single point of intersection, the method should return nu11. Client code can check for this to see if there is a valid intersection point. Parallel lines have no single point of intersection. How do you compute the point of intersection of two lines? - If the two lines have the same slope, there is no single point of intersection. The method retums nu71 in that case. - If neither line is vertical, we have a pair of equations that look like Since both righthand expressions equal y, set them equal to each other: andsolveforx: y=m1x+b1y=m2x+b2m1x+b1=m2x+b2m1xm2x+b1=m2xm2x+b2m1xm2x+b1=b2m1xm2x+b1b1=b2b1m1xm2x=b2b1(m1m2)x=b2b1x=(b2b1)/(m1m2) This final equation x=(b2b1)(m1m2) two lines. coordinate of the intersection directly from the vertical line. You then can plug this x value into the equation for the non-vertical line to compute the intersection point's y coordinate. Be sure that your code works correctly whether the first line or the second line that is vertical. Your intersection method must contain conditional logic to decide from among the possibilities listed above. slope and intercept methods a trivial task.) Regardless, your Line objects must participate correctly with the other code provided. Be prepared to justify your design decision if asked about it. interaction, your project has a problem somewhere. any problems you discover. 5. Additional remarks You may have to fix errors in your existing methods if the new graphical client code reveals logic errors that were not uncovered by earlier tests. 6. Program execution The graphical application allows the user to interactively supply points for lines that potentially intersect. The x-axis ranges from about 300 to +300, and the y-axis ranges from about 300 to +300, so each square on the graph paper is 20 units wide by 20 units high. your implementation of the tostring method in the Line class. Remember, the only files you are supposed to touch are Point. java and Line. java; do not modify the visualGeometry. java file. Some useful interface shortcuts include: - If you wish wish to clear all the points from the graph and make two new lines, press the Esc key. 7. Javadoc Documentation documentation with a web browser. Click this link to explore the results. method in the source code. This works only if the class or method has the necessary Java documentation comments