please help lol

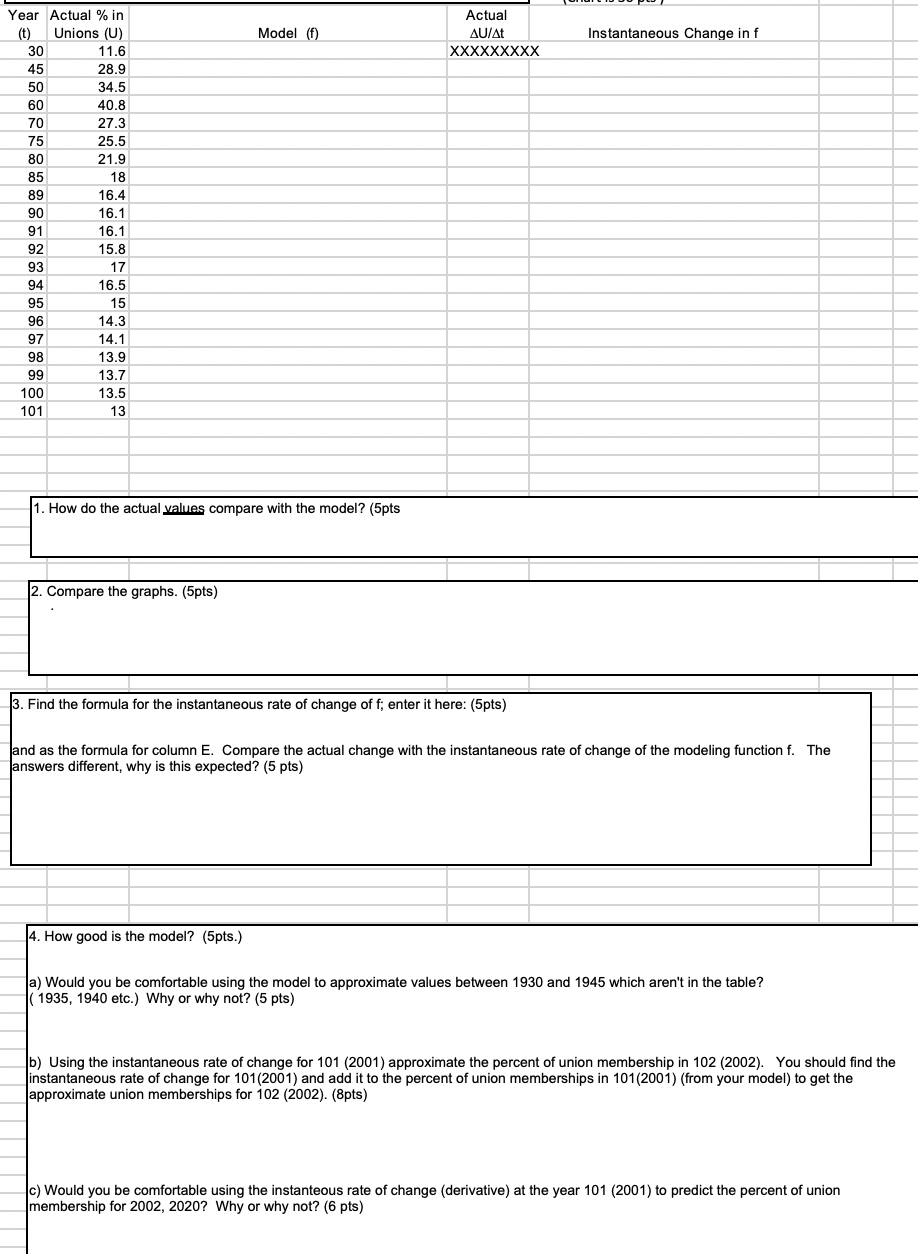
A mathematical model is a mathematical object (often a function or equation) which is used to represent and predict real-world data. In this lab, you're going to look at a mathematical model your text proposes for union membership data from 1930 through 2001, and look at how well it represents two things: the actual percent of union membership, and the changes in that percentage. (Very often, one is more interested in how such an index is changing than in its individual values.) The function your text proposes as a model for the percent of workers in unions for the years 1930 through 2001 is

f(t) = 0.0003869*t^3 - 0.08917*t^2 + 6.2503*t - 102.9

where t is the number of years since 1900. (Thus, f(75) represents the model's value of the percent of workers in unions in 1975.)

Theres 4 parts. - please make a graph on excel after completed all parts.

1. Enter the function above (you can simply use the copy, paste option, starting with the equals sign, after you've inserted the name t for the values in column A on the next sheet) in column C of the next sheet. Then, graph both the actual values of percent union membership and the model. Comment on how the graphs appear to match. (You will probably have to format the axes after you finish the graphs to get better graphs.)

2. Compare the values of the modeling function with the actual values.

3. Compute the instantaneous rate of change of the modeling function in column E (you have to find the derivative formula by hand, and then type this in as your formula for column E) and compare this with the actual rate of change in column D (which you have to find by taking the change in U from the time you're interested in to the next time, and divide by the number of years in between the times, (DU/Dt)).

4. Draw conclusions about how good the model is.

Model (1) Actual U/f XXXXXXXXX Instantaneous Change in f Year Actual % in (t) Unions (U) 30 11.6 45 28.9 50 34.5 40.8 27.3 25.5 21.9 18 16.4 16.1 91 16.1 15.8 17 16.5 15 14.3 14.1 13.9 99 13.7 100 13.5 101 13 95 11. How do the actual values compare with the model? (5pts 2. Compare the graphs. (5pts) 13. Find the formula for the instantaneous rate of change of f; enter it here: (5pts) Jand as the formula for column E. Compare the actual change with the instantaneous rate of change of the modeling function f. The Janswers different, why is this expected? (5 pts) 4. How good is the model? (5pts.) a) Would you be comfortable using the model to approximate values between 1930 and 1945 which aren't in the table? (1935, 1940 etc.) Why or why not? (5 pts) b) Using the instantaneous rate of change for 101 (2001) approximate the percent of union membership in 102 (2002). You should find the instantaneous rate of change for 101(2001) and add it to the percent of union memberships in 101(2001) (from your model) to get the Japproximate union memberships for 102 (2002). (pts) c) Would you be comfortable using the instanteous rate of change (derivative) at the year 101 (2001) to predict the percent of union membership for 2002, 2020? Why or why not? (6 pts) Model (1) Actual U/f XXXXXXXXX Instantaneous Change in f Year Actual % in (t) Unions (U) 30 11.6 45 28.9 50 34.5 40.8 27.3 25.5 21.9 18 16.4 16.1 91 16.1 15.8 17 16.5 15 14.3 14.1 13.9 99 13.7 100 13.5 101 13 95 11. How do the actual values compare with the model? (5pts 2. Compare the graphs. (5pts) 13. Find the formula for the instantaneous rate of change of f; enter it here: (5pts) Jand as the formula for column E. Compare the actual change with the instantaneous rate of change of the modeling function f. The Janswers different, why is this expected? (5 pts) 4. How good is the model? (5pts.) a) Would you be comfortable using the model to approximate values between 1930 and 1945 which aren't in the table? (1935, 1940 etc.) Why or why not? (5 pts) b) Using the instantaneous rate of change for 101 (2001) approximate the percent of union membership in 102 (2002). You should find the instantaneous rate of change for 101(2001) and add it to the percent of union memberships in 101(2001) (from your model) to get the Japproximate union memberships for 102 (2002). (pts) c) Would you be comfortable using the instanteous rate of change (derivative) at the year 101 (2001) to predict the percent of union membership for 2002, 2020? Why or why not? (6 pts)